初中数学中考复习 考点10 一次函数图像与性质（原卷版）

这是一份初中数学中考复习 考点10 一次函数图像与性质（原卷版），共15页。

考点十 一次函数的图像与性质
【命题趋势】
在中考中，主要以选择题、填空题和解答题形式出现，主要考查一次函数的图像与性质，确定一次函数的解析式，一次函数与方程（组）、不等式的关系。一次函数与二次函数、反比例函数综合也是中考重点之一。

【中考考查重点】
一、 结合具体情景体会一次函数的意义，能根据已知条件确定一次函数的表达式；
二、 利用待定系数法确定一次函数的表达式；
三、 根据一次函数画出图像，探索并理解k＞0和k＜0时，图像的变化情况；
四、 体会一次函数与二元一次方程的关系


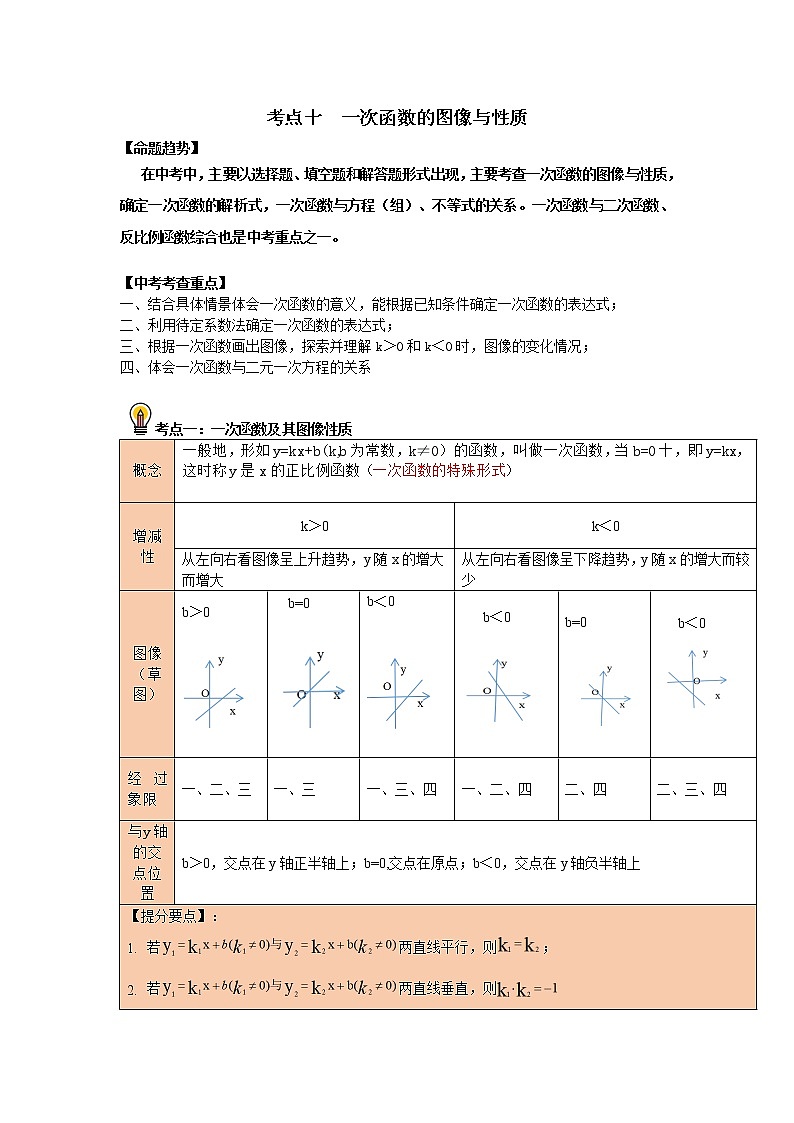
考点一：一次函数及其图像性质
概念
一般地，形如y=kx+b(k,b为常数，k≠0）的函数，叫做一次函数，当b=0十，即y=kx，这时称y是x的正比例函数（一次函数的特殊形式）

增减性
k＞0
k＜0
从左向右看图像呈上升趋势，y随x的增大而增大
从左向右看图像呈下降趋势，y随x的增大而较少
图像（草图）
b＞0

b=0


b＜0



b＜0

b=0

b＜0

经过象限

一、二、三

一、三
一、三、四
一、二、四
二、四
二、三、四
与y轴的交点位置
b＞0，交点在y轴正半轴上；b=0,交点在原点；b＜0，交点在y轴负半轴上
【提分要点】：
1. 若两直线平行，则；
2. 若两直线垂直，则
1．（2021春•大安市期末）一次函数y＝2x﹣1图象经过象限（　　）
A．一、二、三 B．一、二、四 C．二、三、四 D．一、三、四
2．（2021秋•肃州区期末）对于一次函数y＝x+6，下列结论错误的是（　　）
A．函数值随自变量增大而增大
B．函数图象与x轴正方向成45°角
C．函数图象不经过第四象限
D．函数图象与x轴交点坐标是（0，6）
3．（2021秋•东港市期中）点A（﹣1，y1）和点B（﹣4，y2）都在直线y＝﹣2x上，则y1与y2的大小关系为（　　）
A．y1＞y2 B．y1＜y2 C．y1＝y2 D．y1≥y2
4．（2021秋•三水区期末）若一次函数y＝kx+b的图象经过第一、二、四象限，则一次函数y＝bx+k的图象大致是（　　）
A． B．
C． D．
考点二：一次函数解析式的确定
方法
待定系数法
步骤
1. 设：一般式y=kx+b（k≠0）（题干中未给解析式需设）
2. 代：找出一次函数图像上的两个点，并且将点坐标代入函数解析式，得到二元一次方程组；
3. 求：解方程（组）求出k、b的值；
4. 写：将k、b的值代入，直接写出一次函数解析式

5．（2021秋•尤溪县期中）已知一次函数y＝x+b过点（﹣1，﹣2），那么这个函数的表达式为（　　）
A．y＝x﹣1 B．y＝x+1 C．y＝x﹣2 D．y＝x+2
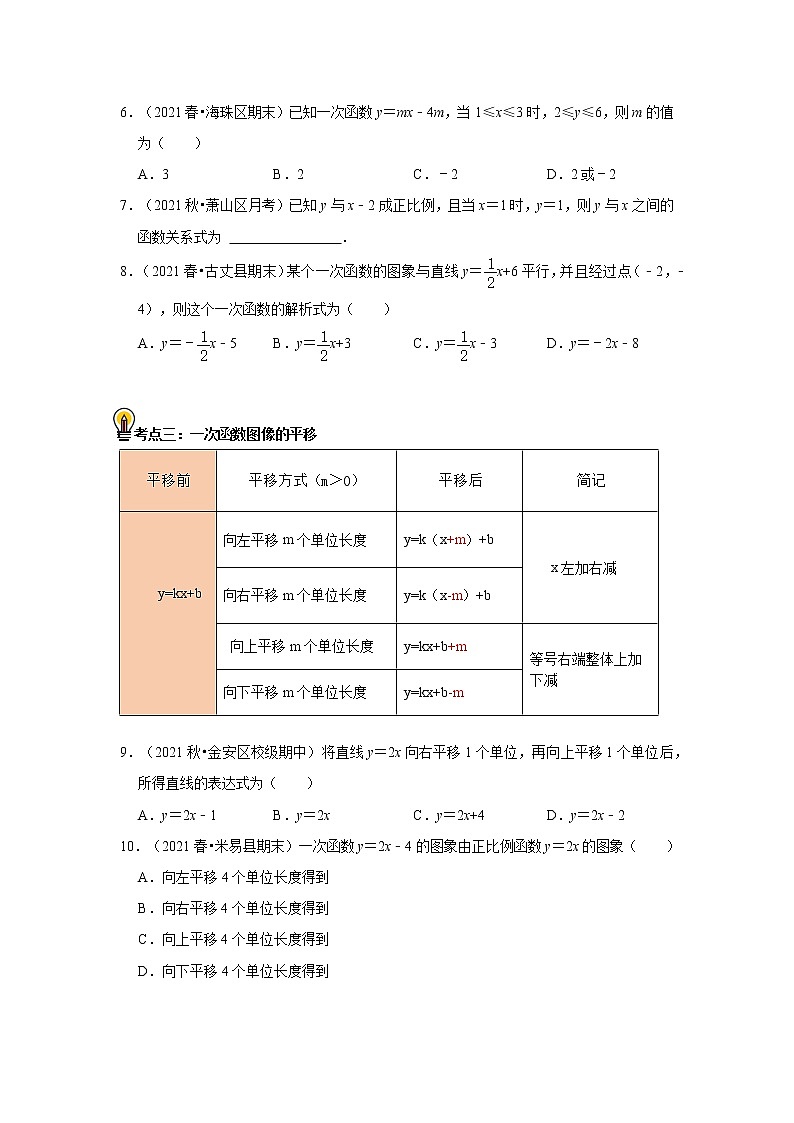
6．（2021春•海珠区期末）已知一次函数y＝mx﹣4m，当1≤x≤3时，2≤y≤6，则m的值为（　　）
A．3 B．2 C．﹣2 D．2或﹣2
7．（2021秋•萧山区月考）已知y与x﹣2成正比例，且当x＝1时，y＝1，则y与x之间的函数关系式为 　　 ．
8．（2021春•古丈县期末）某个一次函数的图象与直线y＝x+6平行，并且经过点（﹣2，﹣4），则这个一次函数的解析式为（　　）
A．y＝﹣x﹣5 B．y＝x+3 C．y＝x﹣3 D．y＝﹣2x﹣8


考点三：一次函数图像的平移
平移前
平移方式（m＞0）
平移后
简记
y=kx+b


向左平移m个单位长度
y=k（x+m）+b
x左加右减
向右平移m个单位长度
y=k（x-m）+b
向上平移m个单位长度
y=kx+b+m
等号右端整体上加下减
向下平移m个单位长度
y=kx+b-m

9．（2021秋•金安区校级期中）将直线y＝2x向右平移1个单位，再向上平移1个单位后，所得直线的表达式为（　　）
A．y＝2x﹣1 B．y＝2x C．y＝2x+4 D．y＝2x﹣2
10．（2021春•米易县期末）一次函数y＝2x﹣4的图象由正比例函数y＝2x的图象（　　）
A．向左平移4个单位长度得到
B．向右平移4个单位长度得到
C．向上平移4个单位长度得到
D．向下平移4个单位长度得到

11．（2021秋•长丰县月考）已知点A（2，4）沿水平方向向左平移3个单位长度得到点A'，若点A'在直线y＝x+b上，则b的值为（　　）
A．1 B．3 C．5 D．﹣1


考点四：一次函数与方程（组）、不等式
与一元一次方程的关系
方程ax+b=0（a≠0）的解是一次函数y=ax+b(a≠0）的函数值为0时自变量的取值，还是直线y=ax+b(a≠0）与x轴交点的横坐标
与二元一次方程组的关系
方程组的解时直线的交点坐标

与一元一次不等式的关系
1. 从“数”来看
（1） kx+b＞0的解集是y=kx+b中，y＞0时x的取值范围
（2） kx+b＞＜0的解集是y=kx+b中，y＜0时x的取值范围
2. 从“形”上看
（1） kx+b＞0的解集是y=kx+b函数图像位于x上方部分对应的点的横坐标
（2） kx+b＜0的解集是y=kx+b函数图像位于x下方部分对应的点的横坐标

12．（2021秋•乐平市期中）一次函数y＝kx+b的图象如图所示，则关于x的方程kx+b＝0的解为（　　）

A．x＝0 B．x＝3 C．x＝﹣2 D．x＝﹣3
13．（2021秋•安徽期中）已知一次函数y＝ax﹣1与y＝mx+4的图象交于点A（3，1），则关于x的方程ax﹣1＝mx+4的解是（　　）
A．x＝﹣1 B．x＝1 C．x＝3 D．x＝4




14．（2021春•沧县期末）如图，直线y＝x+5和直线y＝ax+b相交于点P（20，25），根据图象可知，方程x+5＝ax+b的解是（　　）

A．x＝20 B．x＝5 C．x＝25 D．x＝15
15．（2020秋•建湖县期末）如图，一次函数y＝kx+b（k≠0）的图象经过点A（﹣1，﹣2）和点B（﹣2，0），一次函数y＝2x的图象过点A，则不等式2x＜kx+b≤0的解集为（　　）

A．x≤﹣2 B．﹣2≤x＜﹣1 C．﹣2＜x≤﹣1 D．﹣1＜x≤0
16．（2021秋•兴宁区校级月考）如图，直线y＝kx+b交x轴于点A（﹣2，0），直线y＝mx+n交x轴于点B（5，0），这两条直线相交于点C（2，c），则关于x的不等式组的解集为（　　）

A．x＜5 B．1＜x＜5 C．﹣2＜x＜5 D．x＜﹣2




17．（2020秋•西林县期末）如图所示是函数y＝kx+b与y＝mx+n的图象，则方程组的解是（　　）

A． B． C． D．



1．（2021春•扎兰屯市期末）将直线y＝﹣2x﹣2向右平移1个单位长度，可得直线的表达式为（　　）
A．y＝2x B．y＝﹣2x﹣4 C．y＝﹣2x D．y＝﹣2x+4
2．（2021春•玉田县期末）下列有关一次函数y＝﹣6x﹣5的说法中，正确的是（　　）
A．y的值随着x值的增大而增大
B．函数图象与y轴的交点坐标为（0，5）
C．当x＞0时，y＞﹣5
D．函数图象经过第二、三、四象限
3．（2021春•红寺堡区期末）点P1（x1，y1），点P2（x2，y2）是一次函数y＝﹣4x+3图象上的两个点，且x1＜x2，则y1与y2的大小关系是（　　）
A．y1＞y2 B．y1＞y2＞0 C．y1＜y2 D．y1＝y2
4．（2021秋•运城期中）在平面直角坐标系中，一次函数y＝kx+3（k≠0）的图象经过点A（2，﹣1），则这个一次函数的表达式是（　　）
A．y＝﹣2x+3 B．y＝x+3 C．y＝2x+3 D．y＝x+3


5．（2021秋•南海区期中）如图，一次函数y＝kx+b的图象经过点（2，0）、（0，1），则下列结论正确的是（　　）

A．k＝1
B．关于x的方程kx+b＝0的解是x＝2
C．b＝2
D．关于x的方程kx+b＝0的解是x＝1
6．（2021秋•滕州市期中）直线y＝ax+b（a≠0）过点A（0，2），B（1，0），则关于x的方程ax+b＝0的解为（　　）
A．x＝0 B．x＝2 C．x＝1 D．x＝3
7．（2021秋•龙凤区期末）一次函数y＝mx﹣n（m，n为常数）的图象如图所示，则不等式mx﹣n≥0的解集是（　　）

A．x≥2 B．x≤2 C．x≥3 D．x≤3
8．（2020秋•开化县期末）如图，直线y＝2x+n与y＝mx+3m（m≠0）的交点的横坐标为﹣1，则关于x的不等式2x+n＜mx+3m＜0的整数解为（　　）

A．﹣1 B．﹣2 C．﹣3 D．﹣3.5


9．（2021春•单县期末）已知方程组的解为，则直线y＝﹣x+2与直线y＝2x﹣7的交点在平面直角坐标系中位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
10．（2021春•武陵区期末）对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}＝a；当a＜b时，max{a，b}＝b；如：max{4，﹣2}＝4，max{3，3}＝3，若关于x的函数为y＝max（2x﹣1，﹣x+2}，则该函数的最小值是（　　）
A．2 B．1 C．0 D．﹣1
11．（2020秋•成安县期末）如图，若直线y＝kx+b与x轴交于点A（﹣4，0），与y轴正半轴交于B，且△OAB的面积为4，则该直线的解析式为（　　）

A． B．y＝2x+2 C．y＝4x+4 D．
12．（2021春•饶平县校级期末）已知2y﹣3与3x+1成正比例，则y与x的函数解析式可能是（　　）
A．y＝3x+1 B． C． D．y＝3x+2
13．（2021秋•榆林期末）已知直线l1交x轴于点（﹣3，0），交y轴于点（0，6），直线l2与直线l1关于x轴对称，将直线l1向下平移8个单位得到直线l3，则直线l2与直线l3的交点坐标为（　　）
A．（﹣1，﹣4） B．（﹣2，﹣4） C．（﹣2，﹣1） D．（﹣1，﹣1）







1．（2021•长沙）下列函数图象中，表示直线y＝2x+1的是（　　）
A． B．
C． D．
2．（2021•嘉峪关）将直线y＝5x向下平移2个单位长度，所得直线的表达式为（　　）
A．y＝5x﹣2 B．y＝5x+2 C．y＝5（x+2） D．y＝5（x﹣2）
3．（2021•陕西）在平面直角坐标系中，将直线y＝﹣2x向上平移3个单位，平移后的直线经过点（﹣1，m），则m的值为（　　）
A．﹣1 B．1 C．﹣5 D．5
4．（2021•抚顺）如图，直线y＝2x与y＝kx+b相交于点P（m，2），则关于x的方程kx+b＝2的解是（　　）

A．x＝ B．x＝1 C．x＝2 D．x＝4
5．（2020•牡丹江）两个一次函数y＝ax+b和y＝bx+a，它们在同一个直角坐标系的图象可能是（　　）
A． B．
C． D．
6．（2021•乐山）如图，已知直线l1：y＝﹣2x+4与坐标轴分别交于A、B两点，那么过原点O且将△AOB的面积平分的直线l2的解析式为（　　）

A．y＝x B．y＝x C．y＝x D．y＝2x
7．（2021•娄底）如图，直线y＝x+b和y＝kx+4与x轴分别相交于点A（﹣4，0），点B（2，0），则解集为（　　）

A．﹣4＜x＜2 B．x＜﹣4 C．x＞2 D．x＜﹣4或x＞2
8．（2019•苏州）若一次函数y＝kx+b（k，b为常数，且k≠0）的图象经过点A（0，﹣1），B（1，1），则不等式kx+b＞1的解集为（　　）
A．x＜0 B．x＞0 C．x＜1 D．x＞1

9．（2021•德阳）关于x，y的方程组的解为，若点P（a，b）总在直线y＝x上方，那么k的取值范围是（　　）
A．k＞1 B．k＞﹣1 C．k＜1 D．k＜﹣1
10．（2021•呼和浩特）在平面直角坐标系中，点A（3，0），B（0，4）．以AB为一边在第一象限作正方形ABCD，则对角线BD所在直线的解析式为（　　）
A．y＝﹣x+4 B．y＝﹣x+4 C．y＝﹣x+4 D．y＝4
11．（2019•江西）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣，0），（，1），连接AB，以AB为边向上作等边三角形ABC．
（1）求点C的坐标；
（2）求线段BC所在直线的解析式．














1．（2021•庐阳区校级一模）一次函数y＝﹣2x﹣3的图象和性质．叙述正确的是（　　）
A．y随x的增大而增大
B．与y轴交于点（0，﹣2）
C．函数图象不经过第一象限
D．与x轴交于点（﹣3，0）
2．（2021•陕西模拟）平面直角坐标系中，直线y＝﹣2x+m沿x轴向右平移4个单位后恰好经过（1，2），则m＝（　　）
A．﹣1 B．2 C．﹣4 D．﹣3
3．（2021•商河县校级模拟）若一次函数y＝kx+b的图象经过一、二、四象限，则一次函数y＝﹣bx+k的图象不经过（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4．（2021•萧山区一模）已知y﹣3与x+5成正比例，且当x＝﹣2时，y＜0，则y关于x的函数图象经过（　　）
A．第一、二、三象限 B．第一、二、四象限
C．第一、三、四象限 D．第二、三、四象限
5．（2021•陕西模拟）一次函数y＝kx+b的图象经过点A（2，3），每当x增加1个单位时，y增加3个单位，则此函数表达式是（　　）
A．y＝x+3 B．y＝2x﹣3 C．y＝3x﹣3 D．y＝4x﹣4
6．（2021•蕉岭县模拟）在平面直角坐标系中，一次函数y＝mx+b（m，b均为常数）与正比例函数y＝nx（n为常数）的图象如图所示，则关于x的方程mx＝nx﹣b的解为（　　）

A．x＝3 B．x＝﹣3 C．x＝1 D．x＝﹣1


7．（2021•奉化区校级模拟）八个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（　　）

A．y＝﹣x B．y＝﹣x C．y＝﹣x D．y＝﹣x

8．（2021•遵义一模）如图，直线y＝kx+b（k＜0）与直线y＝x都经过点A（3，2），当kx+b＞x时，x的取值范围是（　　）

A．x＜2 B．x＞2 C．x＜3 D．x＞3
9．（2021•饶平县校级模拟）如图，函数y＝ax+b和y＝﹣x的图象交于点P，则根据图象可得，关于x，y的二元一次方程组中的解是（　　）

A． B． C． D．
10．（2021•杭州模拟）已知直线l：y＝kx+b经过点A（﹣1，a）和点B（1，a﹣4），若将直线l向上平移2个单位后经过原点，则直线的表达式为（　　）
A．y＝2x+2 B．y＝2x﹣2 C．y＝﹣2x+2 D．y＝﹣2x﹣2
11．（2021•南山区校级二模）我国古代很早就对二元一次方程组进行了研究，古著《九章算术》记载用算筹表示二元一次方程组，发展到现代就是用矩阵式＝来表示二元一次方程组，而该方程组的解就是对应两直线（不平行）a1x+b1y＝c1与a2x+b2y＝c2的交点坐标P（x，y）据此，则矩阵式＝所对应两直线交点坐标是　 　．
12．（2021•杭州模拟）已知直线y＝kx+b经过点A（5，0），B（1，4）．
（1）求直线AB的解析式；
（2）若直线y＝2x﹣4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x﹣4＞kx+b的解集．