

专题10 全等三角形(题型归纳)-备战 中考数学一轮复习精品课件与题型归纳专练(全国通用)
展开
这是一份专题10 全等三角形(题型归纳)-备战 中考数学一轮复习精品课件与题型归纳专练(全国通用),文件包含专题10全等三角形题型归纳解析版docx、专题10全等三角形题型归纳原卷版docx等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。
专题10 全等三角形
题型分析
题型演练
题型一 全等三角形的概念
1.(2022·广西·一模)下列说法正确的是( )
A.两个面积相等的图形一定是全等形
B.两个等边三角形是全等形
C.若两个图形的周长相等,则它们一定是全等形
D.两个全等图形的面积一定相等
2.下列说法正确的是( )
A.形状相同的两个三角形是全等三角形
B.全等三角形的周长和面积分别相等
C.所有等腰三角形都是全等三角形
D.所有等边三角形都是全等三角形
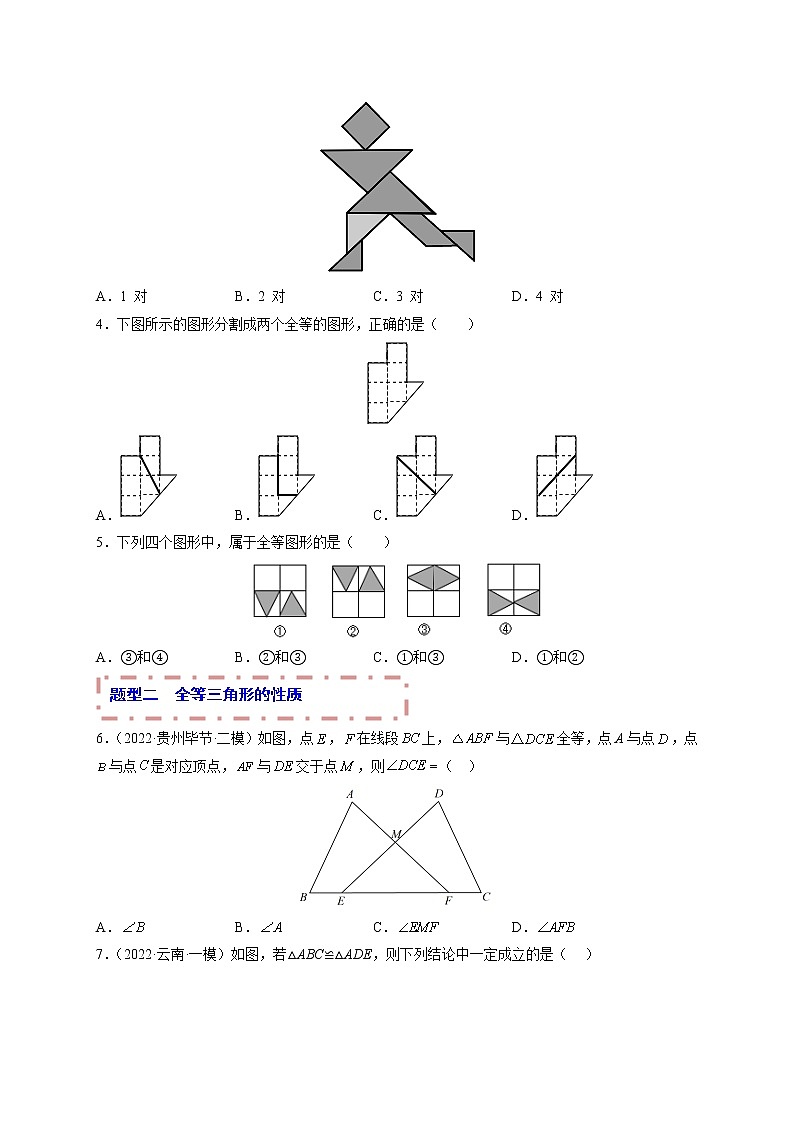
3.(2022·广东·揭西县宝塔实验学校三模)如图是小明用七巧板拼成的一个机器人,其中全等三角形有( )
A.1 对 B.2 对 C.3 对 D.4 对
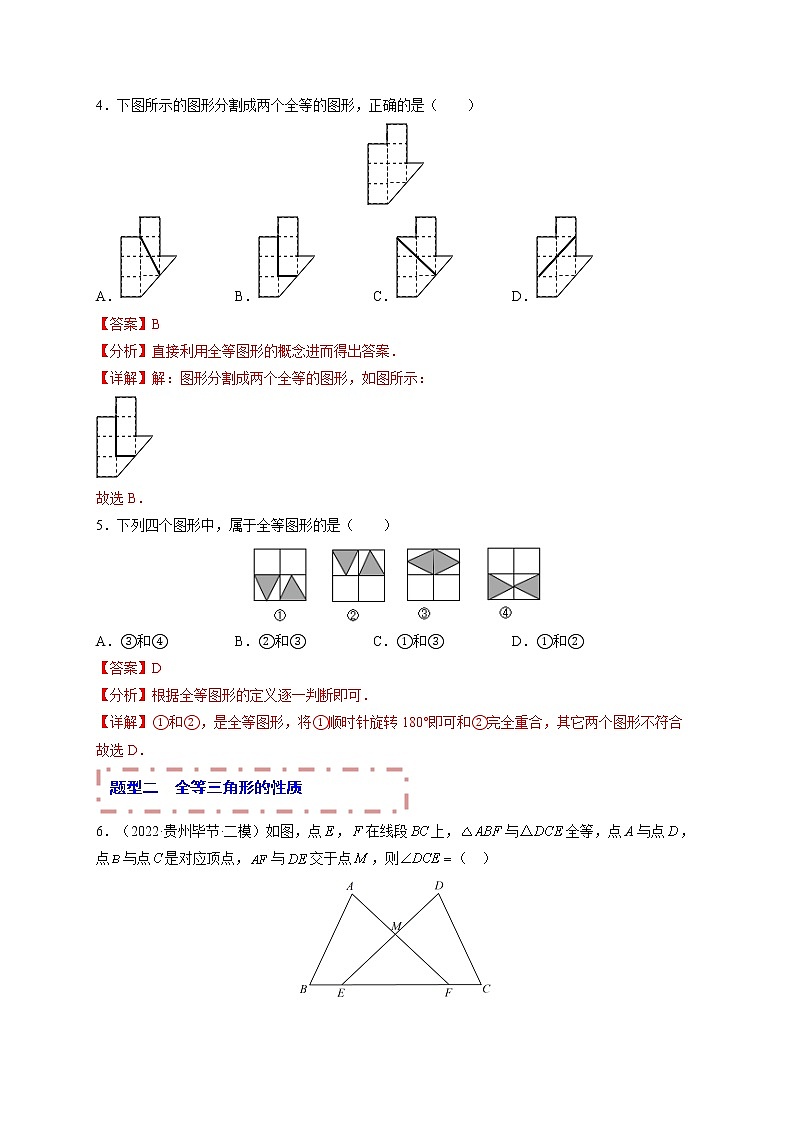
4.下图所示的图形分割成两个全等的图形,正确的是( )
A. B. C. D.
5.下列四个图形中,属于全等图形的是( )
A.③和④ B.②和③ C.①和③ D.①和②
题型二 全等三角形的性质
6.(2022·贵州毕节·二模)如图,点,在线段上,与全等,点A与点,点与点是对应顶点,与交于点,则( )
A. B. C. D.
7.(2022·云南·一模)如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE B.∠BAD=∠CAE C.AB=AE D.∠ABC=∠AED
8.若△ABC≌△DEF,AB=2,AC=4,且△DEF的周长为奇数,则EF的值为( )
A.3 B.4 C.1或3 D.3或5
9.如图,点B、E、A、D在同一条直线上,△ABC≌△DEF,AB=7,AE=2,则AD的长是( )
A.4 B.5 C.6 D.7
10.如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
A.仅① B.仅①③ C.仅①③④ D.仅①②③④
题型三 利用SSS证明三角形全等
11.如图,已知∠AOB,用直尺和圆规按照以下步骤作图:
①以点O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
②画射线O′A',以点O'为圆心,OC长为半径画弧,交O′A'于点C';
③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D';
④过点D′画射线O′B';
根据以上操作,可以判定△OCD≌△O'C'D',其判定的依据是( )
A.SSS B.SAS C.ASA D.HL
12.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( ) .
A.SAS B.ASA C.AAS D.SSS
13.(2022·广东·黄埔学校九年级开学考试)在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0) B.(4,0) C.(4.﹣2) D.(4,﹣3)
14.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在的两边、上分别在取,移动角尺,使角尺两边相同的刻度分别与点、重合,这时过角尺顶点的射线就是的平分线.这里构造全等三角形的依据是( )
A. B. C. D.
15.如图是用直尺和圆规作一个角等于已知角,那么能得出的依据是运用全等三角形判定( )
A.边边边 B.边角边 C.角边角 D.角角边
题型四 利用SAS证明三角形全等
16.为了测量工件的内径,设计了如图所示的工具,点O为卡钳两柄的交点,且有OA=OB=OC=OD,只要量得CD之间的距离,就可知工件的内径AB.其数学原理是利用△AOB≌△COD,判断的依据是( )
A.SSS B.SAS C.ASA D.AAS
17.如图,与相交于点O,,不添加辅助线,判定的依据是( )
A. B. C. D.
18.如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( )
A.∠1=∠DAC B.∠B=∠D C.∠1=∠2 D.∠C=∠E
19.“又是一年三月三”.在校内劳动课上,小明所在小组的同学们设计了如图所示的风筝框架.已知的周长为,.制作该风筝框架需用材料的总长度至少为( )
A. B. C. D.
20.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,要测量工件内槽宽AB,只要测量A′B′就可以,这是利用什么数学原理呢?( )
A.AAS B.SAS C.ASA D.SSS
题型五 利用ASA证明三角形全等
21.如图所示,某同学把一块三角形的模具不小心打碎成了三块,现在要去商店配一块与原来一样的三角形模具,那么最省事的是带哪一块去( )
A.① B.② C.③ D.①和②
22.一块三角形玻璃不慎被小明摔成了四片碎片(如图所示),小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店,就可以让师傅配一块与原玻璃一样的玻璃.你认为下列四个答案中考虑最全面的是( )
A.带其中的任意两块去都可以 B.带1、4或2、3去就可以了
C.带1、4或3、4去就可以了 D.带1、2或2、4去就可以了
23.如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带( )去最省事.
A.① B.② C.③ D.①③
24.如图,已知,添加下列条件中的一个,不能判断的是( )
A. B. C. D.
25.如图,是上一点,交于点,,,若,,则的长是( )
A.0.5 B.1 C.1.5 D.2
题型六 利用HL证明三角形全等
26.数学课上,同学们探讨利用不同画图工具画角的平分线的方法.小旭说:我用两块含30°的直角三角板就可以画角平分线.如图,取OM=ON,把直角三角板按如图所示的位置放置,两直角边交于点P,则射线OP是∠AOB的平分线,小旭这样画的理论依据是( )
A.SSA B.HL C.ASA D.SSS
27.(2022·贵州遵义·三模)已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC②∠BCE+∠BCD=180°③AD=AE=EC ④ BA+BC=2BF其中正确的是( )
A.①②③ B.①③④ C.①②④ D.①②③④
28.(2022·山东济南·模拟预测)如图是标准跷跷板的示意图,横板的中点过支撑点,且绕点只能上下转动.如果,,则小孩玩耍时,跷跷板可以转动的最大角度为( )
A.15° B.20° C.30° D.40°
29.如图,将边长为的正方形ABCD绕点A逆时针方向旋转后得到正方形,则图中阴影部分的面积为( )
A. B. C. D.
30.(2022·浙江温州·一模)如图,在△ABC中,∠BAC=90°,以BC为边向上作正方形BCDE,以AC为边作正方形ACFG,点D落在GF上,连结AE,EG.若DG=2,BC=6,则△AEG的面积为( )
A.4 B.6 C.5 D.8
题型七 尺规作图
31.(2022·广西贵港·三模)尺规作图(保留作图痕迹,不写作法):如图,已知△ABC,请根据“SAS”基本事实,求作△DEF,使△DEF≌△ABC.
32.(2022·广东惠州·二模)如图,已知点E、C在线段BF上,且BE=CF,CM∥DF,
(1)作图:在BC上方作射线BN,使∠CBN=∠1,交CM的延长线于点A(用尺规作图法,保留作图痕迹,不写作法);
(2)在(1)的条件下,求证:AC=DF.
33.(2022·北京市三帆中学模拟预测)已知:如图,在中,.
求作:射线,使得.
下面是小甲同学设计的尺规作图过程.
作法:如图
①以点为圆心,适当长为半径作弧,分别交,于,两点;
②以点为圆心,长为半径作弧,交的延长线于点;
③以点为圆心,长为半径作弧,与中作的弧在内部交于点;
④作射线所以射线就是所求作的射线.
根据小甲同学设计的尺规作图过程,请使用直尺和圆规,补全图形保留作图痕迹,并完成证明.
34.(2022·湖南长沙·模拟预测)人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
已知:.
求作:,使得≌.
作法:如图.
(1)画;
(2)分别以点,为圆心,线段,长为半径画弧,两弧相交于点;
(3)连接线段,,则即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)完成下面证明过程(将正确答案填在相应的横线上):
证明:由作图可知,在和中,
∴≌______.
(2)这种作一个三角形与已知三角形全等的方法的依据是______.(填序号)
①AAS;②ASA;③SAS;④SSS
35.图①、图②均为4×4的正方形网格,每个小正方形的顶点称为格点,线段的端点均在格点上.
(1)在图①中画出以为斜边的等腰直角,使点在格点上;
(2)在图②中画出以为斜边的直角,使点在格点上且与不全等,再在上找到一点,使得最短.(要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法)
题型八 倍长中线模型
36.如图,中,,,为中线,求中线的取值范围.
37.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6
(1)尺规作图:作AB边上的中点D和△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
38.如图,在中,,是边上的中线,延长至,使,求证:.
39.(2022·山东烟台·一模)(1)方法呈现:
如图①:在中,若,,点D为BC边的中点,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使,再连接BE,可证,从而把AB、AC,集中在中,利用三角形三边的关系即可判断中线AD的取值范围是_______________,这种解决问题的方法我们称为倍长中线法;
(2)探究应用:
如图②,在中,点D是BC的中点,于点D,DE交AB于点E,DF交AC于点F,连接EF,判断与EF的大小关系并证明;
(3)问题拓展:
如图③,在四边形ABCD中,,AF与DC的延长线交于点F、点E是BC的中点,若AE是的角平分线.试探究线段AB,AF,CF之间的数量关系,并加以证明.
40.某数学兴趣小组在一次活动中进行了探究试验活动,请你来加入.
【探究与发现】
(1)如图1,AD是的中线,延长AD至点E,使,连接BE,证明:.
【理解与应用】
(2)如图2,EP是的中线,若,,设,则x的取值范围是________.
(3)如图3,AD是的中线,E、F分别在AB、AC上,且,求证:.
题型九 旋转模型
41.(2022·广东汕尾·九年级期中)在中,,,直线经过点,且于点,于点.
(1)当直线绕点旋转到图(1)的位置时,求证:;
(2)当直线绕点旋转到图(2)的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
42.已知等边△ABC,点D为BC上一点,连接AD.
图1 图2
(1)若点E是AC上一点,且CE=BD,连接BE,BE与AD的交点为点P,在图(1)中根据题意补全图形,直接写出∠APE的大小;
(2)将AD绕点A逆时针旋转120°,得到AF,连接BF交AC于点Q,在图(2)中根据题意补全图形,用等式表示线段AQ和CD的数量关系,并证明.
43.如图,在正方形ABCD中,点P在直线BC上,作射线AP,将射线AP绕点A逆时针旋转45°,得到射线AQ,交直线CD于点Q,过点B作BE⊥AP于点E,交AQ于点F,连接DF.
(1)依题意补全图形;
(2)用等式表示线段BE,EF,DF之间的数量关系,并证明.
44.(2022·福建泉州·九年级期中)如图,在中,,为边上的点,且,为线段的中点,过点作,过点作,且、相交于点.
(1)求证:
(2)求证:
45.(2022·河南信阳·九年级期末)如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2,CD=1,求FE的长.
题型十 垂线模型
46.如图,在△ABC中,∠ACB=90°,AC=BC,点E是∠ACB内部一点,连接CE,作AD⊥CE,BE⊥CE,垂足分别为点D,E.
(1)求证:△BCE≌△CAD;
(2)请直接写出AD,BE,DE之间的数量关系: .
47.在中,,,直线MN经过点C,且于D点,于E点.
(1)当直线MN绕点C旋转到图①的位置时,求证:;
(2)当直线MN绕点C旋转到图②、图③的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
48.(2022·安徽·九年级期末)如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为射线CB上一动点,连结AE,作AF⊥AE且AF=AE.
(1)如图1,过F点作FD⊥AC交AC于D点,求证:FD=BC;
(2)如图2,连结BF交AC于G点,若AG=3,CG=1,求证:E点为BC中点.
(3)当E点在射线CB上,连结BF与直线AC交子G点,若BC=4,BE=3,则 .(直接写出结果)
49.(2022·黑龙江牡丹江·九年级期末)平面内有一等腰直角三角板(∠ACB=90°)和一直线MN.过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图1),易证:AF+BF=2CE.
(1)当三角板绕点A顺时针旋转至图2的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
(2)当三角板绕点A顺时针旋转至图3的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,不需证明.
50.(2022·对外经济贸易大学附属中学(北京市第九十四中学)九年级期中)在△ABC中,∠BAC=45°,CD⊥AB于点D,AE⊥BC于点E,连接DE.
(1)如图1,当△ABC为锐角三角形时,
①依题意补全图形,猜想∠BAE与∠BCD之间的数量关系并证明;
②用等式表示线段AE,CE,DE的数量关系,并证明;
(2)如图2,当∠ABC为钝角时,依题意补全图形并直接写出线段AE,CE,DE的数量关系.
题型十一 角平分线性质定理的应用
51.(2022·宁夏·银川北塔中学一模)如图,,以点O为圆心,任意长为半径作弧分别交,于点,,分别以点,为圆心,大于的长为半径作弧,两弧交于点,过点作,于点,若,则的长为( )
A.2.5 B.2 C.1.5 D.1
52.(2022·福建省福州第四十中学九年级开学考试)如图,Rt△ABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若△BCG的面积为4,BC=4,P为AB上一动点,则GP的最小值为( )
A.无法确定 B.4 C.3 D.2
53.(2022·山东泰安·一模)如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3 B.4 C.5 D.6
54.(2022·广东·东莞市光明中学三模)以下不是命题的是( )
A.角平分线上的点到角两边的距离相等 B.定理一定是真命题
C.画线段cm D.全等三角形对应角相等
55.(2022·河北邯郸·三模)在正方形网格中,的位置如图所示,则下列各点中到两边距离相等的点是( )
A.点Q B.点N C.点R D.点M
题型十二 角平分线的判定定理
56.(2022·上海徐汇·二模)如图,两把完全相同的长方形直尺按如图方式摆放,记两把尺的接触点为点P.其中一把直尺边缘恰好和射线OA重合,而另一把直尺的下边缘与射线OB重合,上边缘与射线OA于点M,联结OP.若∠BOP=28°,则∠AMP的大小为( )
A.62° B.56° C.52° D.46°
57.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
58.(2022·贵州铜仁·模拟预测)已知:如图,∠GBC,∠BAC的平分线相交于点F,BE⊥CF于H,若∠AFB=40°,∠BCF的度数为( )
A.40° B.50° C.55° D.60°
59.如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B.8 C.15 D.无法确定
相关试卷
这是一份专题16 与圆有关的计算(题型归纳)-备战 中考数学一轮复习精品课件与题型归纳专练(全国通用),文件包含专题16与圆有关的计算题型归纳解析版docx、专题16与圆有关的计算题型归纳原卷版docx等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
这是一份专题17 相似(题型归纳)-备战 中考数学一轮复习精品课件与题型归纳专练(全国通用),文件包含专题17相似题型归纳解析版docx、专题17相似题型归纳原卷版docx等2份试卷配套教学资源,其中试卷共61页, 欢迎下载使用。
这是一份专题14 与圆有关的性质(题型归纳)-备战 中考数学一轮复习精品课件与题型归纳专练(全国通用),文件包含专题14与圆有关的性质题型归纳解析版docx、专题14与圆有关的性质题型归纳原卷版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。








