2021-2022学年黑龙江省哈尔滨市高一上学期期末学业质量检测数学试题（解析版）

这是一份2021-2022学年黑龙江省哈尔滨市高一上学期期末学业质量检测数学试题（解析版），共16页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
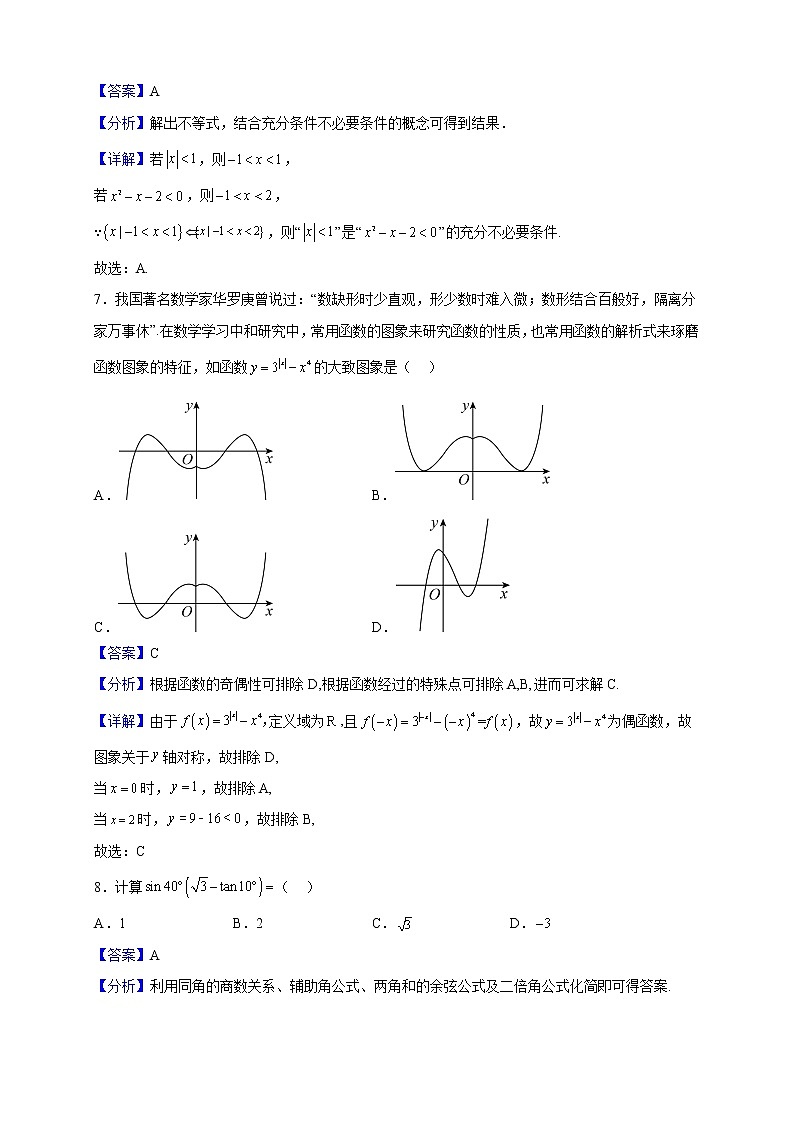
2021-2022学年黑龙江省哈尔滨市高一上学期期末学业质量检测数学试题 一、单选题1．设，，，则（    ）A． B． C． D．【答案】B【分析】先求出然后再求.【详解】又故选：B2．命题“，”的否定是（    ）A．， B．，C．， D．，【答案】C【分析】根据全称命题的否定为特称命题可得答案.【详解】因为全称命题的否定是特称命题，所以命题“，”的否定是“，”.故选：C.3．已知角的终边与单位圆的交点，则（    ）A． B． C． D．【答案】A【分析】利用角的终边与单位圆相交来定义任意角的三角函数值.【详解】因为角的终边与单位圆的交点，令，所以，所以，故选：A.4．哈尔滨地铁某环线12月份地铁票销售总量与时间的关系大致满足，则地铁3号线东南环线前天平均售出（如前10天的平均售出为）的张数最少为（    ）.A．2019 B．2040 C．2021 D．2022【答案】B【分析】求出，再根据基本不等式可求出结果.【详解】地铁3号线东南环线前天平均售出的张数为,由基本不等式可得，当且仅当时，等号成立.所以地铁3号线东南环线前天平均售出的张数最少为张.故选：B5．已知函数，则的值是（    ）A． B． C． D．4【答案】D【分析】根据的范围代入到对应的函数求值即可.【详解】由题意可得，，.故选：D.6．设，则“”是“”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不必要也不充分条件【答案】A【分析】解出不等式，结合充分条件不必要条件的概念可得到结果．【详解】若，则，若，则，∵，则“”是“”的充分不必要条件.故选：A.7．我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休”.在数学学习中和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来琢磨函数图象的特征，如函数的大致图象是（    ）A． B．C． D．【答案】C【分析】根据函数的奇偶性可排除D,根据函数经过的特殊点可排除A,B,进而可求解C.【详解】由于定义域为,且，故为偶函数，故图象关于轴对称，故排除D,当时，，故排除A,当时，，故排除B,故选：C8．计算（    ）A．1 B．2 C． D．【答案】A【分析】利用同角的商数关系、辅助角公式、两角和的余弦公式及二倍角公式化简即可得答案.【详解】解：因为.故选：A. 二、多选题9．下列说法中正确的有（    ）A．奇函数的图象一定经过原点B．若偶函数的图象不经过原点，则它与轴交点的个数一定是偶数C．偶函数的图象关于轴对称D．图象过原点的奇函数必是单调函数【答案】BC【分析】通过反例可知AD错误；根据偶函数的对称性可知BC正确.【详解】对于A，为奇函数，但不经过原点，A错误；对于B，若偶函数图象不经过原点，则其与轴的交点必关于轴对称，则交点个数必为偶数个，B正确；对于C，由偶函数定义知其图象关于轴对称，C正确；对于D，图象过原点且为奇函数，但其在上不单调，D错误.故选：BC.10．将函数的图象向右平移，再把所有点的横坐标伸长到原来的2倍（纵坐标不变）得到函数的图象，则下列说法正确的是（    ）A．函数的图象关于点对称 B．函数在区间上有4个零点C．函数是偶函数 D．函数在区间上最小值是【答案】BC【分析】由已知变换得，利用整体法结合三角函数性质逐个比较判断即可.【详解】的图象向右平移得，则.对A，由，即，则函数的图象关于点 对称，A错；对B，，则，则函数在区间上的零点，共四个，B对；对C，，为偶函数，C对；对D，，则，则当时，函数在区间上取得最小值，为，D错.故选：BC11．已知实数，，满足，则下列结论正确的是（    ）A． B． C． D．【答案】ACD【分析】A选项，根据单调递增，得到；B选项，根据单调性得到，，，结合换底公式得到B错误；C选项，根据的单调性得到；D选项，根据和的单调性，结合中间值比较大小.【详解】A选项，因为单调递增，又，所以，A正确；B选项，因为在单调递增，因为，所以，，故，，即，B错误；C选项，在上单调递减，而，所以，C正确；D选项，因为在单调递减，而，故，因为单调递减，而，故，所以，D正确.故选：ACD12．已知函数，则下列结论正确的是（    ）A．函数有两个零点B．若函数有四个零点，则C．若关于的方程有四个不等实根，则D．若关于的方程有8个不等实根，则【答案】CD【分析】A选项，画出的图象，在同一坐标系内作出的图象，可看出两函数图象有3个交点，A错误；B选项，数形结合得到，B错误；C选项，可看出四个实根有两个根关于对称，另外两个根关于对称，从而得到，C正确；D选项，令，则要有2个不相等的实数根，，得到两根之和，两根之积，化简得到，结合，求出，结合，求出.【详解】A选项，当时，单调递增，当时，单调递减，画出的图象，可以看出关于对称，当时，取得最小值为1，在同一坐标系内作出的图象，可看出两函数图象有3个交点，所以函数有3个零点，A错误；数形结合可得：函数有四个零点，则，B错误；由上图可知：若关于的方程有四个不等实根，不妨设其中关于对称，关于对称，则，所以，C正确；D选项，令，则要有2个不相等的实数根，，且，，，因为，所以，由，解得：，综上：，若关于的方程有8个不等实根，则，D正确. 三、填空题13．已知，则______.【答案】3【分析】利用弦化切即可求出的值.【详解】由，所以即，解得.故答案为：3.14．函数的定义域为______.【答案】【分析】根据被开方数大于等0，分母不为0及对数函数的定义域列出不等式组，求解即可.【详解】由得，解得，所以函数的定义域为.故答案为：.15．已知函数的定义域为R，则实数a的取值范围是______．【答案】【分析】依题意可得恒成立，再分和两种情况讨论，当时，即可得到不等式，解得即可求出参数的取值范围；【详解】解：因为函数的定义域为R，即恒成立，当时恒成立；当时，则，解得；综上可得故答案为：16．已知函数满足，对任意的，都有恒成立，且，则关于的不等式的解集为______.【答案】【分析】由题知以函数为偶函数，且在上单调递减，在上单调递增，再根据讨论求解即可.【详解】解：因为函数满足，即所以函数为奇函数，不妨设，因为对任意的，都有恒成立，所以，，即，所以，函数在上单调递减，因为函数为奇函数，所以函数为偶函数，且在上单调递增，因为，所以，当时，，；当时，，；当时，，；当时，，；所以，关于的不等式的解集为故答案为： 四、解答题17．（1）；（2）.【答案】（1）；（2）.【分析】（1）根据指数幂的运算法则直接求解即可；（2）根据对数运算法则直接化简求解即可.【详解】（1）原式；（2）原式.18．已知函数.(1)求函数的最小正周期；(2)求函数图象的对称轴方程；(3)求函数的单调递减区间.【答案】(1)(2)(3)， 【分析】（1）化简的解析式，然后求得的最小正周期.（2）利用整体代入法求得函数图象的对称轴方程.（3）利用整体代入法求得函数的单调递减区间.【详解】（1），所以的最小正周期.（2）令得，即函数图象的对称轴方程为.（3）令，，解得，，所以函数的单调递减区间是，.19．几年国家出台的惠民政策越来越多，政府出资的“旧房改造”工程使得许多老旧校区旧貌换新颜，从根本上提高了百姓的生活质量.如图，在改造某小区时，要在一处公共区域搭建一间背面靠墙（墙长7米）的房屋，图形所示为房屋俯视图，房屋地面面积为房屋正面的造价为600元，侧面的造价为200元，顶部总造价为4800元，如果墙面高为3m，不计房屋背面和地面的费用，设总造价为元.(1)请将总造价表示为正面边长的函数，怎样设计房屋边长能使总造价最低？最低总造价是多少？(2)如果所需总费用不超过22800元，求房屋正面边长的取值范围是多少？【答案】(1)，当正面墙长为4m时造价最低，最低总造价为19200元.(2) 【分析】（1）写出函数后运用基本不等式可得结果.（2）解分式型不等式可得结果.【详解】（1）设房屋正面墙长为，侧面边长为，总造价为元，则，∴∴，当且仅当即“”时上式取等号. 答：当正面墙长为4m时造价最低，最低总造价为19200元.（2）∵∴，又∵∴不等式变为：，，∴答：房屋正面边长的取值范围是.20．已知函数（其中）.(1)解关于的不等式；(2)若不等式在内恒成立，求实数的取值范围.【答案】(1)答案见解析(2) 【分析】（1）分，，三种情况讨论，从而可得出答案；（2）在内恒成立，即，利用函数的单调性求得的最大值即可得解.【详解】（1）不等式，即，当时，，不等式的解集为， 当时，，可得，当，则，所以不等式的解集为，若，则，所以不等式的解集为，综上所述，当时，不等式的解集为，当时，不等式的解集为，当时，不等式的解集为；（2）不等式在内恒成立，即，有在内恒成立，即求在的最大值，令，，设，则，因为，所以，，所以，即，所以在上单调递增，，所以在的最大值为，故，所以实数的取值范围是.21．(1)若，求的值；(2)若当时，关于的不等式有解，求实数的取值范围.【答案】(1)(2) 【分析】（1）先化简，再把待求式化为，代入求值；（2）利用单调性求出，即可求解.【详解】（1）若，即则.（2）由题意可知，不等式有解，即，因为，所以，因为在上单调递增，在上单调递减，故当，即时取得最大值，且最大值∴.即实数的取值范围为.22．已知函数，其中.(1)设.若对任意实数，恒成立，求实数的取值范围；(2)是否存在实数，使得且，若存在，求的取值范围；若不存在说明理由.【答案】(1)(2)存在，理由见解析 【分析】（1）问题转化为，，根据函数的单调性求出最小值为-4，故得到不等式，求出实数的取值范围；（2）考虑，，三种情况，前两种情况不合要求，时，转化为有负实数解，，分与，求出的取值范围.【详解】（1）依题，恒成立，∴，，∵在上单调递增，∴时，，∴，即，∴或故实数的取值范围是；（2）①当时，与矛盾，∴舍去，②当时，由，得，此时，∴，∴，∵，∴，又，∴时无解，∴时，不存在实数，使得且成立；③当时，由，得，此时，∴，∴若有解有负实数解，设，∵且，∴必有负实数解，对于可化为，当，即时，不成立；当时，可化为，∵，∴，即，∴，且，∴，综上所述，存在实数，使得且.