2022-2023学年广东实验中学高一上学期期末数学试题（解析版）

这是一份2022-2023学年广东实验中学高一上学期期末数学试题（解析版），共20页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
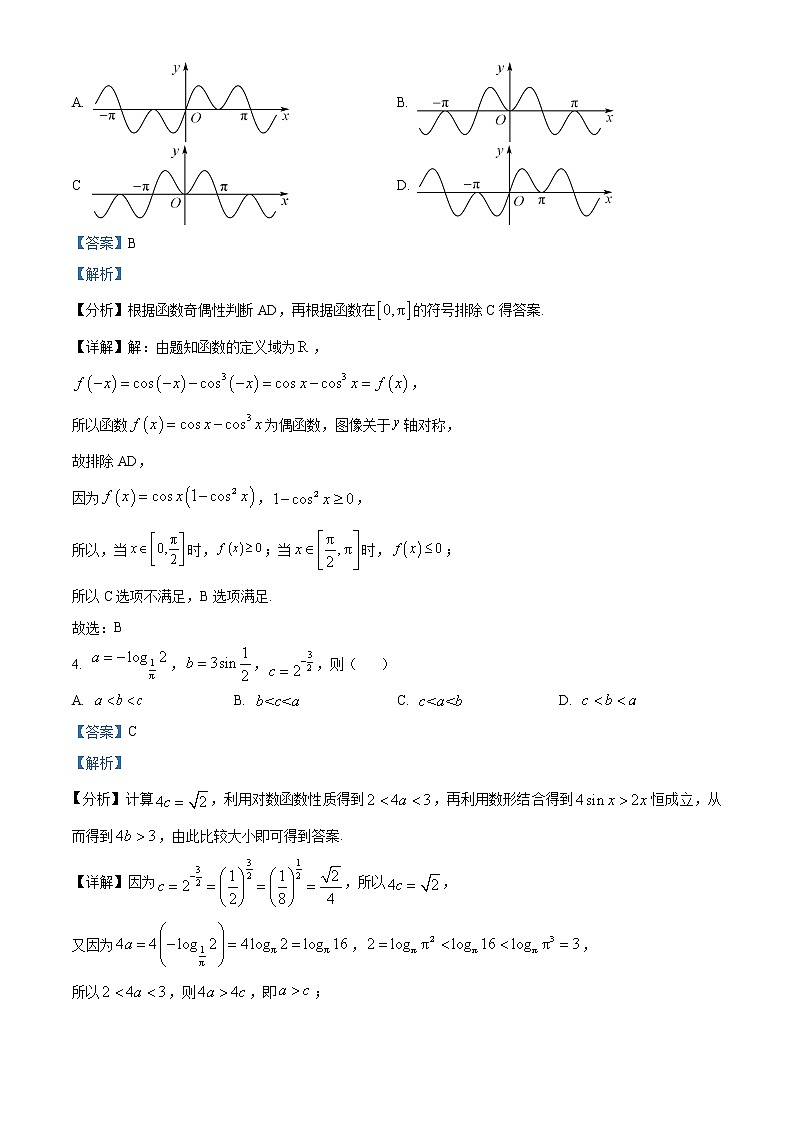
高一上期末限时训练数学考试时间：90分钟  全卷总分：120分一、单选题（共6小题，每小题5分）1. 设全集，集合，则（    ）A.  B.  C.  D. 【答案】A【解析】【分析】解二次不等式，结合自然数集的概念化简全集，再利用集合的补集运算即可得解.【详解】因为，所以，则，故，所以全集，因，所以.故选：A.2. 已知为第二象限角，且，则的值为（    ）A. -25 B.  C.  D. 【答案】C【解析】【分析】由题知，进而根据正切的差角公式展开求解即可.【详解】解：因为为第二象限角，且，所以，所以故选：C3. 函数的图像大致为（    ）A.  B. C  D. 【答案】B【解析】【分析】根据函数奇偶性判断AD，再根据函数在的符号排除C得答案.【详解】解：由题知函数的定义域为，，所以函数为偶函数，图像关于轴对称，故排除AD，因为，，所以，当时，；当时，；所以C选项不满足，B选项满足.故选：B4. ，，，则（    ）A.  B.  C.  D. 【答案】C【解析】分析】计算，利用对数函数性质得到，再利用数形结合得到恒成立，从而得到，由此比较大小即可得到答案.【详解】因为，所以，又因为，，所以，则，即；作出与的图像，如图，易知当时，，当时，，所以在上恒成立，.所以，故，即；综上：，即.故选：C5. 鸡仔饼是广州的一种特色小吃，属粤菜系，是广东四大名饼之一.为了实现鸡仔饼销售100万元的利润目标，某商家准备制定激励销售人员的奖励方案：在销售利润超过6万元时，按销售利润进行奖励，且奖金（单位：万元）随销售利润（单位：万元）的增加而增加，但奖金总数不超过3万元，同时奖金不能超过利润的20%.同学们利用函数知识，设计了如下函数模型，其中符合这一商家要求的是（    ）参考数据：A.  B. C.  D. 【答案】A【解析】【分析】根据函数的单调性以特殊函数值求解.【详解】对于A, 满足，增函数，，构造，，因为，所以，且，所以，即，所以在单调递减，所以，所以的图象恒在图象的下方，即奖金不超过利润20%，满足题意，A正确；对于B，当时，，不满足题意，B错误；对于C，，，则，，因为，所以不满足单调递增，C错误；对于D，当时，，不满足题意，D错误；故选:A.6. 已知，若函数在上无零点，则不可能为第（    ）象限角.A. 一 B. 二 C. 三 D. 四【答案】B【解析】【分析】利用三角恒等变换将问题转化为方程无解，从而得到或，由此利用正弦函数的性质与辅助角公式即可得解.【详解】因为，令，则，因为，所以，则，所以，又，所以，故，因为在上无零点，所以在上无解，因为，所以，所以或，当时，由于，所以，因为，所以；当时，，则，即，故，因为，所以，故，则；综上：或，所以不可能为第二角限角.故选：B.【点睛】关键点睛：本题的突破口是将问题转化为无解，从而熟练掌握三角函数的性质即可得解.二、多选题（共2小题，每小题5分）7. 函数的部分图像如图所示，则下列结论正确的是（    ）A. 的最小正周期为B. 是图像的一个对称中心C. 在区间上单调递增D. 把图像上所有点向右平移个单位长度后得到函数的图像【答案】AB【解析】【分析】根据正弦型函数的性质、图像的变换性质，结合已知图像逐一判断即可.【详解】解：由题意知，，，所以周期，，又，所以，即因为，所以令，即，所以，，故A选项正确；当时，，即是图像的一个对称中心，故B选项正确；对于C选项，因为，所以，由于正弦函数在其上单调递减，所以函数在上单调递减，故C选项错误；将图像上所有点向右平移个单位长度后得到的图像，故D选项错误.故选：AB8. 已知函数，若方程有六个相异实根，则实数可能的取值为（    ）A.  B.  C.  D. 【答案】CD【解析】【分析】画出的图像，结合图像，将问题转化为在上有两个相异实根，再由一元二次函数根的分布列出不等式组，即可求出答案.【详解】因为，所以当时，，所以，故，所以，其图像由先沿着轴向左平移1个单位，再沿着轴上下翻转，去掉上的图像而得，当时，，易得开口向下，对称轴为，且，所以作出的图像，如图，.令，故要使方程有六个相异实根，则需使在上有两个相异实根，所以，解得，故，对于AB，经检验，易知选项AB不满足要求，故AB错误；对于C，因为，所以，则，故，故C正确；对于D，因为，所以，即，故，又，所以，则，故D正确.故选：CD.【点睛】方法点睛：函数零点的求解与判断有以下方法，（1）直接求零点：令，如果能求出解，则有几个解就有几个零点；（2）零点存在性定理：利用定理不仅要函数在区间上是连续不断的曲线，且，还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点；（3）利用图象交点的个数：将函数变形为两个函数的差，画两个函数的图象，看其交点的横坐标有几个不同的值，就有几个不同的零点．三、填空题（共4小题，每小题5分）9. 若命题：，，则的否定为___________命题（填“真”或“假”）.【答案】真【解析】【分析】直接写出其否定为，使得，即可判断其真假.【详解】由题得命题的否定为，使得，显然此命题为真命题，故答案为：真.10. 古代文人墨客与丹青手都善于在纸扇上题字题画，题字题画的部分多为扇环、已知某扇形的扇环如图所示，其中外弧线的长为48cm，内弧线的长为16cm，连接外弧与内弧的两端的线段均为20cm，则该扇形的中心角的弧度数为____________.【答案】【解析】【分析】根据扇形弧长与扇形的中心角的弧度数的关系，求得，进而可得该扇形的中心角的弧度数.【详解】依题意，如图，弧的长为，弧的长为，，设扇形的中心角的弧度数为，则，所以，则，因为，又，所以，所以该扇形的中心角的弧度数．故答案为：..11. 已知，，则的最小值为____________.【答案】【解析】【分析】结合基本不等式求解即可.【详解】解：因为，，所以，当且仅当且，即时等号成立，所以的最小值为故答案为：12. 已知函数图像的两条相邻对称轴之间的距离小于，，且，则的最小值为_____________.【答案】【解析】【分析】先利用三角恒等变换化简，再由题设条件推得，从而推得，再利用基本关系式求得，由此求得的最小值.【详解】因为，其中，由题意可得，又，所以，因为，则为的最值，所以，所以，故，当时，，；当时，，；所以，所以，因为，所以，所以，即，所以，因为，所以，解得（负值舍去），所以，故，所以，又因为，所以的最小值为.故答案为：.【点睛】关键点睛：本题的突破口是充分利用辅助角的值，结合三角函数的基本关系式求得值，从而确定的范围.四、解答题（共5小题，60分）13. 已知非空集合，，全集.（1）当时，求；（2）若“”是“”的必要条件，求实数a的取值范围.【答案】（1）；    （2）.【解析】【分析】（1）求出集合，再求出，从而可求；（2）根据题设条件可得，从而可得关于参数的不等式组，从而可求参数的取值范围.【小问1详解】当时，，而，故故.【小问2详解】因为非空，故即.因为“”是“”的必要条件，故，故，故.14. 已知函数.（1）求函数的最小正周期和单调减区间；（2）求不等式的解集.【答案】（1）；    （2）【解析】【分析】先利用三角恒等变化化简，再利用正弦函数的性质即可得解.【小问1详解】因为，所以的最小正周期为，令，得，所以的单调减区间为.【小问2详解】因为，即，所以，则，所以的解集为.15. 已知函数（为常数，）.（1）讨论函数的奇偶性；（2）若方程在上有实根，求实数的取值范围.【答案】（1）答案见解析    （2）【解析】【分析】（1）直接使用奇偶性的定义进行求解；（2）由题知在上有实根，令，则在上有实根，进而在上有实根，再令，则在上有实根，最后根据基本不等式得即可得答案.【小问1详解】解：函数的定义域为，又①当时，即时，可得即当时，函数为偶函数；②当时，即时，可得即当时，函数为奇函数；③当时，函数为非奇非偶函数．综上，当时，函数为偶函数；当时，函数为奇函数；当时，函数为非奇非偶函数．【小问2详解】解：因为方程在上有实根，所以在上有实根，所以在上有实根，令，所以在上有实根，所以在上有实根因为，，所以，在上有实根，因为，所以在上有实根令，所以在上有实根，因为，当且仅当，即时等号成立，当时，，时，，所以，所以，在上有实根，则所以，实数的取值范围是16. 如图，在直径为1的圆中，作一关于圆心对称、邻边互相垂直的十字形，其中.（1）将十字形的面积表示成的函数；（2）求十字形面积的最大值，并求出此时的值.【答案】（1）    （2），此时【解析】【分析】（1）设十字形面积为，易知，然后将代入求解.， （2）由（1）的结论，利用二倍角的正弦和余弦公式，结合辅助角公式得到，再利用正弦函数的性质求解.【小问1详解】解：如图所示：，为锐角，因为，所以，解得，所以，【小问2详解】解：由（1）知，（其中），当，，即当时，十字形取得最大面积，．因为所以此时，所以综上，，此时17. 已知函数，，且，，.（1）求实数的值，并写出函数的定义域；（2）试讨论函数的最值；（3）若，求实数的取值范围.【答案】（1），的定义域为    （2）详见解析    （3）【解析】【分析】（1）根据对数运算，待定系数得，进而解不等式组即可得其定义域；（2）首先将函数转化为关于的二次函数，再利用换元，讨论定义域与对称轴的关系，结合函数的单调性，求函数的最值；（3）结合函数的图象以及函数的定义域，确定恒成立，根据（2）中函数的最值，列不等式求解.【小问1详解】因为，且，所以所以，解得，所以，所以，即，解得所以，的定义域为；【小问2详解】，令，所以函数的最值即为函数，的最值，所以，当时，，最小值为，最大值为，当时，对称轴，所以函数在区间单调递增，函数的最小值为，最大值；当时，对称轴，函数在区间单调递增，函数的最小值为，最大值；当时，对称轴，函数的最大值是，函数的最小值是；当时，对称轴，函数的最大值是，最小值是.综上可知：当时，最小值为，最大值；当时，最小值为，最大值；当时，函数的最大值是，函数的最小值是；当时，函数的最大值是，最小值是.【小问3详解】画出函数的图象，且函数在单调递减，且，当时，，当时，，若，则恒成立，且由函数的定义域可知，函数在上恒成立，由（2）可知，函数的最小值大于0，即，得，当时，最大值，得，则； 当时，函数的最大值，解得：；综上可知，.【点睛】关键点睛：本题考查函数与三角函数的综合应用，本题的难点在第三问，关键是确定函数的单调性，并且注意隐含条件，从而确定恒成立，转化为关于最值的不等式.