最新中考数学二次函数压轴300题终极突破提升训练（18）

这是一份最新中考数学二次函数压轴300题终极突破提升训练（18），文件包含中考数学二次函数压轴300题终极突破提升训练18解析版docx、中考数学二次函数压轴300题终极突破提升训练18原卷版docx等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

中考数学二次函数压轴300题终极突破提升训练（18）

1．已知抛物线的顶点为点，与轴分别交于、两点（点在点的左侧），与轴交于点．
（1）直接写出点的坐标为________；
（2）如图，若、两点在原点的两侧，且，四边形为正方形，其中顶点、在轴上，、位于抛物线上，求点的坐标；
（3）若线段，点为反比例函数与抛物线在第一象限内的交点，设的横坐标为，当时，求的取值范围．

【答案】（1）；（2）；（3）
【分析】（1）把函数变形为顶点式即可求解；
（2）设A（x1，0），B（x2，0），易得x1＋x2＝−2，又OA＝3OB得到−x1＝3x2，求出x1，x2，得到A，B坐标，将B（1，0）代入抛物线求出a，设E（m，0），则，EN＝−（m2＋2m−3），根据题意，得 2m＋2＝−（m2＋2m−3），解得m的值即可求解；
（3）由线段AB＝2，得A（−2，0），B（0，0），a＝4，y＝4x2＋8x，当1＜m＜3时，对于抛物线y＝4x2＋8x，y随x的增大而增大，对于反比例函数，y随x的增大而减小，当x＝1时，双曲线在抛物线上方，即＞4×12＋8×1，解得k＞12，当x＝3时，双曲线在抛物线下方，即＜4×32＋8×3，解得k＜180，所以k的取值范围12＜k＜180．
【详解】（1）∵y＝ax2＋2ax＋a−4＝a（x＋1）2−4，
∴P（−1，−4）；
故答案为：（−1，−4）；
（2）设点，
∵抛物线的对称轴为
∴
则
又
∴
∴
得，
∴A（−3，0），B（1，0），
把点代入得
解得
∴
设点坐标为，F（n,0）
∴，∴n=-m-2
∴，
根据题意得
解得，（舍去）
∴点的坐标为；
（3）∵，抛物线的对称轴为
所以，，
把（0，0）代入得，
解之得，，
∴，
当，对于抛物线来说，随增大而增大；
对于，随增大而减小，所以当时，双曲线在抛物线的上方，
即，解之得，
当时，双曲线位于抛物线的下方，即，解之得，
所以的取值范围为．
【点评】本题是函数综合题，熟练运用二次函数的图像与性质及反比例函数的性质是解题的关键．
2．如图，已知二次函数的图象与轴相交于两点（点在点的左边），与轴交于点，点在二次函数的图像上，且∥轴．问线段BC上是否存在点P，使△POC为等腰三角形；如果存在，求出点P的坐标；如果不存在，请说明理由．

【答案】存在，点或或．
【分析】由抛物线解析式可得出C、B坐标，利用待定系数法可得直线BC的解析式为y=-x-3，分三个情况讨论：当时，点P在OC的垂直平分线上，根据O、C坐标可得OC中点坐标，把OC中点的横坐标代入BC解析式即可得P点坐标；当时，设P（x，-x-3），利用两点间距离公式即可得P点坐标；当时，利用利用两点间距离公式即可得P点坐标．
【详解】当时，，
解得：，
∵点在点的左边，
∴
当x=0时，y=-3，
∴B（0，-3），
设直线BC的函数解析式为
∴，
解得，
∴直线BC的解析式为y=-x-3，
①当时，点P在OC的垂直平分线上，
∵点C（-3，0），O（0，0），
∴OC中点坐标为（，0），
把x=代入y=-x-3得：y=-3=，
∴点
②当时，设P（x，-x-3），
∴=3，
解得：x1=0，x2=-3（舍去），
∴-x-3=-3，
∴点，
③当时，设点，
∴，
解得，（不合题意，舍去）
∴
∴存在，点或或．
【点评】本题考查二次函数图象上的点的坐标特征、待定系数法求一次函数解析式及等腰三角形的判定，注意分类讨论思想的运用是解题关键．
3．如图，抛物线过坐标原点和，两点．
（1）求该抛物线的表达式；
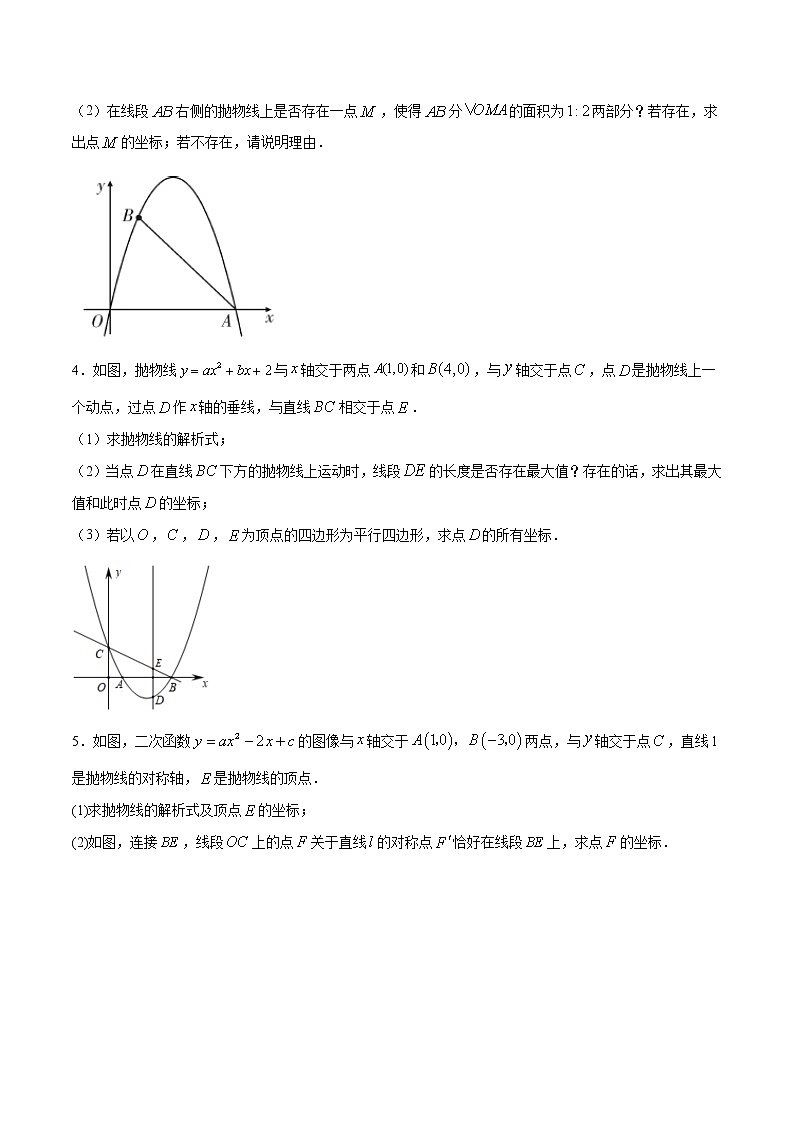
（2）在线段右侧的抛物线上是否存在一点，使得分的面积为两部分？若存在，求出点的坐标；若不存在，请说明理由．

【答案】（1）；（2）存在，点的坐标为，．
【分析】（1）将点、A、B的坐标代入抛物线表达式，即可求解；
（2）先求AB直线的解析式，再证明，设点坐标为，表示出Q点坐标，分①当时，②当时，求出M的坐标.
【详解】解：（1）将点，，的坐标代入抛物线表达式得，
，
解得：，
抛物线的表达式为：；
（2）存在，理由如下：
设直线的表达式为：，
，，
，解得：．
直线的表达式为：，
令，则，
直线交轴于点，如图

设交于点，
当或时，分的面积为，
过点作轴交于点，
，
，
，
，
由点在抛物线上，可设点坐标为，
由点在直线上，则点坐标为，
①当时，则有：，解得：，
由，
即，解得：，
即，，
②当时，则有：，
解得：，
由，
所得方程无解，
综上所述，点的坐标为，．
【点评】本题考查的是二次函数综合运用，涉及到一次函数、三角形相似、三角形的面积计算等，其中（2）要注意分类求解，避免遗漏，难度较大，是中考的常考题型.
4．如图，抛物线与轴交于两点和，与轴交于点，点是抛物线上一个动点，过点作轴的垂线，与直线相交于点．
（1）求抛物线的解析式；
（2）当点在直线下方的抛物线上运动时，线段的长度是否存在最大值？存在的话，求出其最大值和此时点的坐标；
（3）若以，，，为顶点的四边形为平行四边形，求点的所有坐标．

【答案】（1）；（2）存在，DE取最大值2， D（2，﹣1）；（3）点D的坐标是（2，﹣1）或或．
【分析】(1)利用待定系数法求解可得；
(2)设点D坐标为(m，)，则E点的坐标为(m，)，求得DE关于m的函数关系式，根据二次函数的性质即可求解；
(3)分点D在DE上方和下方两种情况，用的代数式表示出DE的长度，依据DE=2得出关于的方程，解之可得
【详解】(1)把点A(1，0)、B(4，0)代入，得：
，
解得，
∴抛物线的解析式是；
(2)存在．
对于二次函数，
令，则，
∴点C的坐标为(0，2)，
设直线BC的解析式为y＝kx+t，
把点B(4，0)，C(0，2)代入y＝kx+t，得：
，
解得，
∴；
设点D的坐标为，则点E的坐标为，
∴，
∴当m＝2时，DE取最大值2，
此时，
∴点D的坐标为(2，﹣1)；
(3)①当D在E下方时，
由(2)得：，
∵点C的坐标为(0，2)，
∴OC＝2，
∵OC∥DE，
∴当DE＝OC时，四边形OCED为平行四边形，
则，
解得m＝2，
此时点D的坐标为(2，﹣1)；
②当D在E上方时，，
同理，当DE＝OC时，四边形OCED为平行四边形，
即，
解得，
∴此时或，
综上所述，点D的坐标是(2，﹣1)或或时，都可以使O，C，D，E为顶点的四边形为平行四边形．
【点评】本题是二次函数的综合问题，考查了待定系数法求函数解析式，二次函数的性质及平行四边形的判定与性质等知识点，要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．
5．如图，二次函数的图像与轴交于两点，与轴交于点，直线l是抛物线的对称轴，是抛物线的顶点．
(1)求抛物线的解析式及顶点的坐标；
(2)如图，连接，线段上的点关于直线的对称点恰好在线段上，求点的坐标．

【答案】(1) ，(-1，4)；(2)
【分析】(1)将点、代入即可求得抛物线的解析式，继而求得顶点的坐标；
(2)利用待定系数法求得直线的解析式，设点，利用对称性得到点的坐标为，将代入直线的解析式，即可求解．
【详解】(1)把点，代入，
得，
解之得．
∴抛物线的解析式为．
当时，，
∴顶点的坐标为(-1，4)；
(2)设直线的解析式为，
把，代入得，
，
解得．
∴直线的解析式为．
设点F的坐标为，
∵抛物线的对称轴为，
∴点的坐标为，
把代入得：
，
解得：，
∴点F的坐标为．
【点评】本题为二次函数的综合应用，涉及待定系数法、轴对称、一次函数、二次函数的性质，熟练掌握二次函数的性质是解本题的关键．
6．已知：如图，抛物线与轴交于点，，与轴交于点．

（1）求抛物线的解析式；
（2）如图，点是线段上方抛物线上的一个动点，连结、．设的面积为．点的横坐标为．
①试求关于的函数关系式；
②请说明当点运动到什么位置时，的面积有最大值？
③过点作轴的垂线，交线段于点，再过点做轴交抛物线于点，连结，请问是否存在点使为等腰直角三角形？若存在，请直接写出点的坐标；若不存在，请说明理由．
【答案】（1）；（2）①，②当m=3时，S有最大值，③点P的坐标为（4,6）或（，）．
【分析】（1）由 ，则-12a=6，求得a即可；
（2）①过点P作x轴的垂线交AB于点D，先求出AB的表达式y=-x+6，设点 ，则点D（m，-m+6），然后再表示即可；
②由在中，＜0，故S有最大值；
③△PDE为等腰直角三角形，则PE=PD，然后再确定函数的对称轴、E点的横坐标，进一步可得|PE|=2m-4，即求得m即可确定P的坐标．
【详解】解：（1）由抛物线的表达式可化为，
则-12a=6，解得：a=，
故抛物线的表达式为：；
（2）①过点P作x轴的垂线交AB于点D，

由点A(0,6)、B的坐标可得直线AB的表达式为：y=-x+6，
设点 ，则点D（m，-m+6），
∴；
②∵，＜0
∴当m=3时，S有最大值；
③∵△PDE为等腰直角三角形，
∴PE=PD，
∵点，函数的对称轴为：x=2，则点E的横坐标为：4-m，
则|PE|=2m-4，
即，
解得：m=4或-2或或（舍去-2和）
当m=4时，=6；
当m=时，=．
故点P的坐标为（4,6）或（，）．
【点评】本题属于二次函数综合应用题，主要考查了一次函数、等腰三角形的性质、图形的面积计算等知识点，掌握并灵活应用所学知识是解答本题的关键．
7．如图，抛物线C1的图象与x轴交A（−3，0），B（1，0）两点，与y轴交于点C（0，3），点D为抛物线的顶点．
（1）求抛物线C1的解析式和D点坐标；
（2）将抛物线C1关于点B对称后的抛物线记为C2，点E为抛物线C2的顶点，求抛物线C2的解析式和E点坐标；
（3）是否在抛物线C2上存在一点P，在x轴上存在一点Q，使得以D，E，P，Q为顶点的四边形是平行四边形，若存在求出P点坐标，若不存在请说明理由．

【答案】（1）抛物线C1的解析式为-x2-2x+3；点D的坐标为（-1,4）；（2）抛物线C2的解析式为y=（x－3）2－4；E点坐标（3，-4）；（3）存在，点P的坐标为（3＋，8）或（3－，8）或（5,0）
【分析】（1）设抛物线C1的解析式为y=a（x＋3）（x－1），将点C的坐标代入即可求出抛物线C1的解析式，化为顶点式即可求出点D的坐标；
（2）根据点的对称性求出点E的坐标，从而求出抛物线C2的解析式；
（3）根据DE为平行四边形的边和对角线分类讨论，分别画出对应的图形，根据平行四边形的性质和点的平移规律即可求出结论．
【详解】解：（1）∵抛物线C1的图象与x轴交A（−3，0），B（1，0）两点
可设抛物线C1的解析式为y=a（x＋3）（x－1）
将点C的坐标代入，得
3=a（0＋3）（0－1）
解得：a=-1
∴抛物线C1的解析式为y=-（x＋3）（x－1）=-x2-2x+3=-（x＋1）2+4
∴抛物线C1的顶点D的坐标为（-1,4）；
（2）将抛物线C1关于点B对称后的抛物线记为C2，点E为抛物线C2的顶点，设C2与x轴的另一交点为K，如下图所示

∴抛物线C2的二次项系数为1
∵点D（-1,4），B（1,0）
∴抛物线C2的顶点E的坐标为（3，-4）
∴抛物线C2的解析式为y=（x－3）2－4；
（3）存在，
由对称性可知：BK=AB=1－（-3）=4
∴点K的坐标为（5,0）
①当DE为平行四边形的边时，
∴DP∥EQ，DP=EQ，即EQ可看作DP平移得到
∵点D（-1,4）到点E（3，-4）的平移方式为：先向右平移4个单位，再向下平移8个单位
∴点P到点Q的平移方式为：先向右平移4个单位，再向下平移8个单位
∵点Q在x轴上
∴点P的纵坐标为8
将y=8代入C2的解析式中，解得：x=3±
∴此时点P的坐标为（3＋，8）或（3－，8）；
②当DE为平行四边形的对角线时，
由DE的中点为点B，
∴PQ的中点也为点B，
由点Q在x轴上，点B也在x轴上
∴点P也在x轴上，即此时点P与点K重合
∴此时点P的坐标为（5,0）；
综上：点P的坐标为（3＋，8）或（3－，8）或（5,0）．

【点评】此题考查的是二次函数的综合大题，掌握利用待定系数法求二次函数解析式、旋转的性质、点的平移规律和平行四边形的性质是解题关键．
8．如图，△AOB的三个顶点A、O、B分别落在抛物线C1：y＝x2＋x上，点A的坐标为(﹣4，m)，点B的坐标为(n，﹣2)．（点A在点B的左侧）
（1）则m＝　 　，n＝　 　．
（2）将△AOB绕点O逆时针旋转90°得到△A′OB′，抛物线C2：y＝ax2＋bx＋4经过A′、B′两点，延长OB′交抛物线C2于点C，连接A′C．设△OA′C的外接圆为⊙M．
①求圆心M的坐标；
②试直接写出△OA′C的外接圆⊙M与抛物线C2的交点坐标（A′、C除外）．

【答案】（1）﹣4；﹣1；（2）①(6，2)；②(0，4)或(12，4)
【分析】（1）把x＝﹣4代入抛物线C1解析式求得y即得到点A坐标；把y＝﹣2代入抛物线C1解析式，解方程并判断大于﹣4的解为点B横坐标；
（2）①根据旋转90°的性质特点可求点A′、B′坐标（过点作x轴垂线，构造全等得到对应边相等）及OA的长，用待定系数法求抛物线C2的解析式，求出直线OC的解析式，构建方程组确定点C的坐标，求出线段OA′，线段A′C的垂直平分线的解析式，构建方程组解决问题即可．
②设⊙M与抛物线C2的交点为P(m，m2﹣3m＋4)．根据PM＝OM，构建方程求解即可．
【详解】解：解：（1）当x＝﹣4时，y＝×（﹣4）2＋×（﹣4）＝﹣4，
∴点A坐标为(﹣4，﹣4)，
当y＝﹣2时，x2＋x＝﹣2，
解得：x1＝﹣1，x2＝﹣6，
∵点A在点B的左侧，
∴点B坐标为(﹣1，﹣2)，
∴m＝﹣4，n＝﹣1．
故答案为﹣4；﹣1；
（2）①如图1，过点B作BE⊥x轴于点E，过点B′作B′G⊥x轴于点G．

∴∠BEO＝∠OGB′＝90°，OE＝1，BE＝2，
∵将△AOB绕点O逆时针旋转90°得到△A′OB，
∴OB＝OB′，∠BOB′＝90°，
∴∠BOE＋∠B′OG＝∠BOE＋∠OBE＝90°，
∴∠B′OG＝∠OBE，
在△B′OG与△OBE中，
，
∴△B′OG≌△OBE（AAS），
∴OG＝BE＝2，B′G＝OE＝1，
∵点B′在第四象限，
∴B′(2，﹣1)，
同理可求得：A′(4，﹣4)，
∴OA＝OA′＝＝4＝4，
∵抛物线C2：y＝ax2＋bx＋4经过点A′、B′，
∴，
解得：，
∴抛物线C2解析式为：y＝x2﹣3x＋4，
∵直线OB′的解析式为y＝﹣x，
由，
解得或，
∴点C(8，﹣4)，
∵A′(4，﹣4)，
∴A′C∥x轴，
∵线段OA′的垂直平分线的解析式为y＝x﹣4，
线段A′C的垂直平分线为x＝6，
∴直线y＝x﹣4与x＝6的交点为(6，2)，
∴△OA′C的外接圆的圆心M的坐标为(6，2)．
②设⊙M与抛物线C2的交点为P(m，m2﹣3m＋4)．
则有（m﹣6）2＋（m2﹣3m＋2）2＝62＋22，
解得m＝0或12或4或8，
∵A′、C除外，
∴P(0，4)或(12，4)．
【点评】此题考查的是二次函数与几何图形的综合大题，难度较大，掌握全等三角形的判定及性质、利用待定系数法求二次函数、一次函数解析式、三角形外接圆的性质是解题关键．
9．如图，抛物线L：yx2x﹣12与x轴正半轴交于点A，与y轴交于点B．
（1）求直线AB的解析式及抛物线顶点坐标；
（2）如图1，点P为第四象限且在对称轴右侧抛物线上一动点，过点P作PC⊥x轴，垂足为C，PC交AB于点D，求PD+BD的最大值，并求出此时点P的坐标；
（3）如图2，将抛物线L：yx2x﹣12向右平移得到抛物线，直线AB与抛物线交于M，N两点，若点A是线段MN的中点，求抛物线的解析式．

【答案】（1）直线AB解析式为y＝3x－12，抛物线顶点坐标为（，－）；（2）PD＋BD的最大值为，此时点P的坐标为（，）；（3）抛物线的解析式为y＝2x2－13x＋6．
【分析】（1）先求出点A，点B坐标，利用待定系数法可求解析式，通过配方法可求顶点坐标；
（2）设点P（x，2x2－5x－12）（＜x＜4），则点D（x，3x－12），由两点距离公式可求PD，BD的长，可得PD＋BD＝－2x2＋8x＋x＝－2（x－）2＋，由二次函数的性质可求解；
（3）设平移后的抛物线L'解析式为y＝2（x－m）2－，联立方程组可得x2－2（m＋）x＋m2－＝0，设点M（x1，y1），点N（x2，y2），可得x1＋x2＝2（m＋），由中点坐标公式可得x1＋x2＝8，可求m的值，即可求解．
【详解】解：（1）∵抛物线L：y＝2x2－5x－12与x轴正半轴交于点A，与y轴交于点B，
∴点A（4，0），点B（0，－12），
设直线AB解析式为：y＝kx－12，
∴0＝4k－12，
∴k＝3，
∴直线AB解析式为：y＝3x－12，
∵y＝2x2－5x－12
＝2（x－）2－，
∴抛物线顶点坐标为（，－）；
（2）∵点A（4，0），点B（0，－12），
∴OA＝4，OB＝12，
∴AB＝＝＝，
设点P（x，2x2－5x－12）（＜x＜4），则点D（x，3x－12），
∴BD＝＝x，
PD＝（3x－12）－（2x2－5x－12）＝－2x2＋8x，
∴PD＋BD＝－2x2＋8x＋x
＝－2（x－）2＋，
∵＜x＜4，－2＜0，
∴当x＝时，PD＋BD有最大值为，
此时，点P（，）；
（3）设平移后的抛物线解析式为y＝2（x－m）2－，
联立方程可得：2（x－m）2－＝3x－12，
∴x2－2（m＋）x＋m2－＝0，
设点M（x1，y1），点N（x2，y2），
∵直线AB与抛物线L'交于M，N两点，
∴x1，x2是方程x2－2（m＋）x＋m2－＝0的两根，
∴x1＋x2＝2（m＋），
∵点A是MN的中点，
∴x1＋x2＝8，
∴2（m＋）＝8，
∴m＝，
∴平移后的抛物线解析式为y＝2（x－）2－
即：y＝2x2－13x＋6．
【点评】本题是二次函数综合题，考查了待定系数法求解析式，二次函数的性质，平移的性质，根与系数关系，中点坐标公式等知识，利用参数m列出方程是本题的关键．
10．如图，在平面直角坐标系中，直线交轴于点，交轴于，抛物线经过点、，且与轴交于另一点．

（1）求抛物线的解析式；
（2）点为第一象限内抛物线上一动点，过点作轴于点，交直线于点，设点的横坐标为．
①过点作于点，设的长度为，请用含的式子表示，并求出当取得最大值时，点的坐标．
②在①的条件下，当直线到直线的距离等于时，请直接写出符合要求的直线的解析式．
【答案】（1）；（2）①，点坐标为，②或．
【分析】（1）根据直线BC求出点B、C的坐标，用待定系数法即可求出抛物线解析式；

（2）①过点作于点，推出，再设点，，得出PE后即可得出答案；②根据①z中得出的h值，代入两直线的距离公式即可．
【详解】解：（1）在直线中，令，得；令，得，
∴、
把点，的坐标代入抛物线解析式中，得

解得
∴抛物线解析式为
（2）①如解图，过点作于点.

∴
∵，
∴
∴
又∵
∴
∵
∴是等腰直角三角形
∴
设点，
∴
则
即：.
∴当时，取得最大值
此时点坐标为
②直线BC的解析式为：

直线的解析式为：
由题意可得，两直线间的距离为：
根据两直线间的距离公式可得：
解得：
直线的解析式为：或．
【点评】本题考查了二次函数的综合题：熟练掌握二次函数的性质和轴对称的性质；会利用待定系数法求函数解析式；理解坐标与图形性质，要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度是解题的关键．
11．如图，二次函数的图象与轴交于，，与轴交于点．
（1）求该二次函数的解析式及点的坐标；
（2）如图1，点为抛物线段一动点，于点，轴交于点，当的长度最大时，求点的坐标．
（3）点为抛物线上一点，过作轴交直线于点，点为轴上一点，点为坐标系内一点，当以点，，，为顶点的四边形是正方形时，直接写出点的坐标．

【答案】（1），；（2）；（3），，
【分析】（1）先求出二次函数的解析式，即可得到结果；
（2）设轴于点，，求出，根据直角三角形性质得到，求出直线AC的解析式，得到，求出，即可得到结果；
（3）由题意可得：MN∥EF，设M点的坐标为，即可得到N的点，再根据正方形的性质，分类讨论即可；
【详解】解：（1）∵的图象与轴交于，
∴
∴
∴
当时，
∴
（2）设轴于点，
∵，
∴
在中，
∵，
∴
∴
设直线的解析式为：
∴
∴
∴
∴
即当时最大．
∴．

（3）设M点的坐标为，
则点N的坐标为，
∴MN的长度为
①当MN为直角边时，可知MN∥EF，
∴E，F均在x轴上，
∴M，N点到x轴的距离为，即
∵MNEF为正方形，
∴，
即，
解得，
当x=3时，M点为A点，应舍去
∴M点可为
②当MN是对角线时，
得到，此时E点为MN的垂直平分线与x轴的交点
且△ENM为直角等腰三角形，故MN的长度应该为M到x轴的距离的2倍
得到
解得，，
同理x=3时应舍去
故M点可为，
故综上M点坐标可为，，
【点评】本题主要考查了二次函数的综合应用，结合正方形的性质是解题的关键．
12．如图，直线与抛物线相交于和，点P是线段AB上异于A、B的动点，过点P作轴于点D，交抛物线于点C
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求为直角三角形时点P的坐标

【答案】（1）；（2）存在，；（3）或
【分析】（1）已知B（4，m）在直线y=x+2上，求得m的值，抛物线图象上的A、B两点坐标，通过待定系数法即可求得解析式；
（2）设出P点横坐标，根据直线AB和抛物线的解析式表示出P、C的纵坐标，可得到关于PC与P点横坐标的函数关系式，再化成顶点式即可；
（3）当△PAC为直角三角形时，根据直角顶点的不同，有三种情形，需要分类讨论，分别求解即可．
【详解】（1）∵在直线上，
∴，
∴，
∵、在抛物线上，
∴，解得，
∴抛物线的解析式为．
（2）设动点P得坐标为，则C点得坐标为，
∴，
∵，
∴当时，线段PC最大且为．
（3）∵为直角三角形，
①若点A为直角顶点，．由题意易知，，，因为此种情形不存在；
②若点A为直角顶点，则．
如图1，过点作于点N，则，．过点A作，交x轴于点M，则由题意易知，为等腰直角三角形，
∴，
∴，
∴．
设直线AM得解析式为，则：，解得，所以直线AM得解析式为：
又抛物线得解析式为：②
联立①②式，解得：或（与点A重合，舍去）
∴，即点C、M点重合．当时，，
∴；③若点C为直角顶点，则．
∵，
∴抛物线的对称轴为直线．
如图2，作点关于对称轴得对称点C，则点C在抛物线上，且，当时，．
∵点、均在线段AB上，
∴综上所述，为直角三角形时，点P得坐标为或．

【点评】考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识，解题关键是学会用分类讨论的思想思考问题．
13．抛物线（为常数，且）的顶点为 ，抛物线与轴交于点，对称轴与 轴交于点．
（1）当时，求 、两点坐标；
（2）若点的纵坐标比点的纵坐标大． ①求抛物线的解析式； ②将①中抛物线向上平移个单位长度，得到新的抛物线，在新得到的抛物线上有两点，，当时，有，求 x1 的取值范围；
（3）如图，已知 、在反比例函数图象上，若抛物线与线段有公共点，直接写出的取值范围

【答案】（1），
（2）①；②
（3）a≥或a≤-5
【分析】（1）把a=1代入抛物线解析式，再化成顶点式即可得到答案；
（2）①化抛物线解析式为，求出A点坐标，根据x=0，求出B点坐标，再根据“点的纵坐标比点的纵坐标大”列出方程求出a的值即可得到抛物线的解析式；
②二次函数的性质可知，若，则；
（3）分a＞0和a＜0两种情况讨论即可解答．
【详解】解：（1）当 时，
当时，
，
（2）①

当 时，

根据题意得
解得
抛物线的解析式为；
②新抛物线解析式为
，对称轴为直线，关于对称轴 对称的对称点
根据二次函数的性质可知，若，则；
（3）∵D（2，3）在反比例函数图象上，
∴k=2×3=6
∴
∵(6,m) 在反比例函数上，
∴E(6,1)
分a＞0和a＜0两种情况讨论：
①当a＞0时，如图①，

当x=6时，y=36a-24a+3a-2=15a-2≥1
解得，a≥；
②当a＜0时，如图②，
∵
∴
解得，a≤-5，
综上所述，a的取值范围为a≥或a≤-5．
【点评】本题考查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征；会利用待定系数法求二次函数解析式；会利用分类讨论的思想解决数学问题；本题难度较大，综合性较强．
14．在平面直角坐标系中，点O为坐标原点，抛物线y=﹣x2+（k﹣1）x+k（k＞0）交x轴的负半轴于点A，交x轴的正半轴于点B，交y轴的正半轴于点C，且AB=4．
（1）如图1，求k的值；
（2）如图2，点D在第一象限的抛物线上，点E在线段BC上，DE//y轴，若DE=BE，求点D的坐标；
（3）如图3，在（2）的条件下，F为抛物线顶点，点P在第四象限的抛物线上，FP交直线DE于点Q，点G与点D关于y轴对称，若GQ=DP，求点P的坐标．

【答案】（1）3；（2）D（2，3）；（3）P（1+，﹣1）．
【分析】（1）令y=0，求得A、B两点的坐标，根据AB=4列出k的方程，便可求得k的值；
（2）用待定系数法求出直线BC的解析式，再设D点的横坐标为m，用m表示DE与BE，再由DE=BE，列出m的方程，便可求得结果；
（3）由点F、P的坐标得，直线PF的表达式为，求出点Q（2，），由GQ=DP，列出n的方程，即可求解．
【详解】（1）令y=0，得，
解得，，或，
∴A（，0），B（，0），
∵AB=4，
∴，
∴；
（2）由（1）知，抛物线的解析式为：，B（3，0），
令，得，
∴C（0，3），
设直线BC的解析式为（k≠0），则
把B（3，0）代入得：，
解得，，
∴直线BC的解析式为，
设D点的坐标为（，），则E（，），
∴DE==，
BE=，
∵DE=BE，
∴ ，
解得，或（舍），
∴D（2，3）；
（3）点G与点D关于y轴对称，则点G（-2，3），
，
∴抛物线的顶点F的坐标为（1，4），
设点P（，），
由点F、P的坐标，同理求得直线PF的表达式为，
当时，，
故点Q（2，），
则=，
=，
∵GQ=DP，
∴，
解得（舍去负值），
故点P（，）．
【点评】本题是二次函数与几何的综合题，主要考查了待定系数法求二次函数的解析式和一次函数的解析式．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．
15．如图，抛物线与x轴交于点A，B，与y轴交于点C，其中点B的坐标为，点C的坐标为，直线1经过B，C两点．
（1）求抛物线的解析式；
（2）过点C作轴交抛物线于点D，过线段CD上方的抛物线上一动点E作交线段BC于点F，求四边形ECFD的面积的最大值及此时点E的坐标；
（3）点P是在直线l上方的抛物线上一动点，点M是坐标平面内一动点，是否存在动点P，M，使得以C，B，P，M为顶点的四边形是矩形？若存在，请直线写出点P的横坐标；若不存在，请说明理由．

【答案】（1）；（2），；（3）存在，或1．
【分析】（1）将点，点代入中，即可求解析式；
（2）求出BC的直线解析式为，设，则，所以，即可求面积的最大值；
（3）设，①当时，，可求P点横坐标；②当时，，可求P点横坐标．
【详解】解：（1）将点，点代入中，
则有，
，
；
（2），
对称轴为，
轴，
，
，
点，点，
的直线解析式为，
设，
交线段BC于点F，
，
，
当时，四边形ECFD的面积最大，最大值为；
此时；
（3）设，
①当时，
，
，
，
，
点横坐标为1；
②当时，
，
，
或（舍），
点横坐标为．
综上所述：P点横坐标为或1．
【点评】本题考查二次函数的性质；熟练掌握二次函数的图象及性质，掌握矩形的性质是解题的关键．