

2022-2023学年上海市金山中学高二(上)期末数学试卷(含答案解析)
展开2022-2023学年上海市金山中学高二(上)期末数学试卷
1. 已知复数是虚数单位,则z的虚部为______.
2. 直线与直线的夹角大小等于______.
3. 函数的定义域为______.
4. 函数的最大值为______.
5. 已知集合,,若,则实数a的值为______.
6. 已知函数的图像关于原点对称,且时,,则______.
7. 直线l过点且与圆相切,那么直线l的方程为______.
8. 已知空间中三点,,,则以向量、为一组邻边的平行四边形的面积为______.
9. 已知椭圆C:的面积公式为,若抛物线上到焦点的距离为2的一点P在椭圆C:上,则该椭圆面积的最小值为______.
10. 已知矩形ABCD,P是矩形内一点,且P到AB的距离为若将矩形ABCD绕AD顺时针旋转,则线段AP扫过的区域面积为______.
11. 已知圆M:,圆N:直线、分别过圆心M、N,且与圆M相交于A,B两点,与圆N相交于C,D两点,点P是椭圆上任意一点,则的最小值为______.
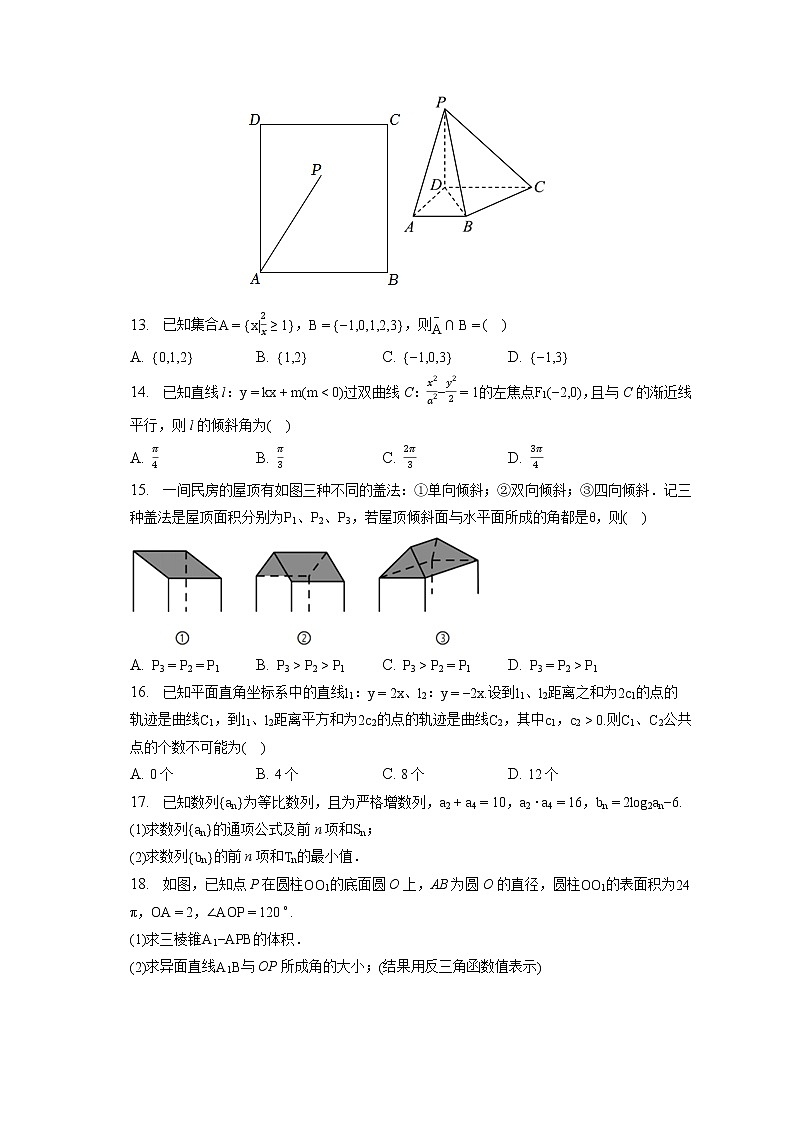
12. 如图,在四棱锥中,平面ABCD,,,,,直线PA与平面ABCD成角.设四面体PBCD外接球的圆心为O,则球的体积为______.
13. 已知集合,,则( )
A. B. C. D.
14. 已知直线l:过双曲线C:的左焦点,且与C的渐近线平行,则l的倾斜角为( )
A. B. C. D.
15. 一间民房的屋顶有如图三种不同的盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法是屋顶面积分别为、、,若屋顶倾斜面与水平面所成的角都是,则( )
A. B. C. D.
16. 已知平面直角坐标系中的直线:、:设到、距离之和为的点的轨迹是曲线,到、距离平方和为的点的轨迹是曲线,其中,则、公共点的个数不可能为( )
A. 0个 B. 4个 C. 8个 D. 12个
17. 已知数列为等比数列,且为严格增数列,,,
求数列的通项公式及前n项和;
求数列的前n项和的最小值.
18. 如图,已知点P在圆柱的底面圆O上,AB为圆O的直径,圆柱的表面积为,,
求三棱锥的体积.
求异面直线与OP所成角的大小;结果用反三角函数值表示
19. 椭圆的左、右焦点分别为,,其中,O为原点.椭圆上任意一点到,距离之和为
求椭圆的标准方程及离心率;
过点的斜率为2的直线l交椭圆于A、B两点.求的面积.
20. 如图,在四棱锥中,已知平面ABCD,且四边形ABCD为直角梯形,,,
证明:;
线段CP上是否存在一点M,使得直线AM垂直平面PCD,若存在,求出线段AM的长,若不存在,说明理由;
点Q是线段BP上的动点,当直线CQ与DP所成的角最小时,求线段BQ的长.
21. 已知,函数的图象为曲线、B是上的两点,A在第一象限,B在第二象限.设点、
若B到和到直线的距离相等,求p的值;
已知,证明:为定值,并求出此定值用p表示;
设,且直线OA、OB的斜率之和为求原点O到直线AB距离的取值范围.
答案和解析
1.【答案】2
【解析】解:复数,
则,即其虚部为
故答案为:
根据共轭复数的定义,以及虚部的定义,即可求解.
本题主要考查共轭复数的定义,以及虚部的定义,属于基础题.
2.【答案】arctan2
【解析】解:的斜率为2,倾斜角为,
的斜率为0,倾斜角为,
故两直线的夹角为
故答案为:
求出两直线的倾斜角,从而得到夹角的大小.
本题主要考查了直线的倾斜角与斜率关系,还考查了两直线的夹角的求解,属于基础题.
3.【答案】且
【解析】解:要使原函数有意义,则,解得且
函数的定义域为且
故答案为:且
由根式内部的代数式大于等于0,分式的分母不为0联立不等式组求解.
本题考查函数的定义域及其求法,是基础题.
4.【答案】2
【解析】解:,
所以函数的最大值为
故答案为:
利用辅助角公式化简函数解析式,由正弦函数的的性质即可求解最值.
本题主要考查三角函数的最值,两角和的正弦的应用,考查运算求解能力,属于基础题.
5.【答案】
【解析】解:集合,,,
则,解得,
当时,直线与重合,不符合题意,
当时,直线与不重合,符合题意,
故实数a的值为
故答案为:
根据已知条件,结合直线平行的性质,即可求解.
本题主要考查交集及其运算,属于基础题.
6.【答案】
【解析】解:根据题意,时,,则,
又由函数的图像关于原点对称,即函数为奇函数,
则,
故答案为:
根据题意,由函数的解析式求出的值,又由奇函数的定义可得函数为奇函数,则有,由此可得答案.
本题考查函数奇偶性的性质以及应用,涉及函数值的计算,属于基础题.
7.【答案】,
【解析】解:直线l过点且与圆相切,
圆的圆心,半径,
当直线的斜率k不存在时,
直线l的方程为,与圆相切,成立;
当直线的斜率k存在时,
设直线方程为,即,
圆心到直线的距离,
解得,,即
综上,直线l的方程为,
故答案为:,
当直线的斜率k不存在时,直线l的方程为,与圆相切,成立;当直线的斜率k存在时,设直线方程为,圆心到直线的距离,求出斜率k,由此能出直线l的方程.
本题考查圆的切线方程的求法,考查圆、直线方程、点到直线距离公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.
8.【答案】
【解析】解:,,,
,,,,
,
,
故答案为:
求出向量的坐标,进而可得模长即向量的夹角,由此可计算以AB,AC为边的平行四边形的面积.
本题考查向量背景下平行四边形的面积的计算,关键是求向量的坐标及模长.
9.【答案】
【解析】解:设P的坐标为,
又P到抛物线的交点的距离为2,
,又,
,将其代入,可得,
,又点P在椭圆C:上,
,当且仅当时,等号成立,
,
椭圆C的面积公式为,
故答案为:
根据抛物线的性质,基本不等式,即可求解.
本题考查抛物线的性质,基本不等式的应用,属中档题.
10.【答案】
【解析】解:线段AP扫过的区域面积即为以为半径,
母线长为的圆锥的侧面积的,故;
故答案为:
由题可得线段AP扫过的区域为圆锥的侧面,再根据圆锥侧面积公式求解即可.
本题考查圆锥的侧面积,考查学生的运算能力,属于中档题.
11.【答案】8
【解析】解:由题意可得,,,,
,
,
为椭圆上的点,
由题意可知,,
,
故答案为:
由题意可知,,,结合P为椭圆上的点,可用P的坐标表示,然后结合椭圆的性质即可求解
本题主要考查了平面向量数量积的运算及基本不等式的应用,属于知识的简单综合应用.
12.【答案】
【解析】解:在底面ABCD上,,,,,
所以,所以,
在上,,
由余弦定理可得:,
所以,所以
所以
又因为平面ABCD,所以
又,面PBD,面PBD
所以面PBD,所以
则和均为直角三角形,当O点为PC中点时,,
此时O为四面体PBCD的外接球的球心.
直线PA与平面ABCD成角,平面ABCD,
则,,
又,
四面体PBCD外接球的半径为,
所以四面体PBCD外接球的体积为
故答案为:
先证明出和均为直角三角形,得到O点位置,可求得外接球的半径,可求其体积.
本题考查四面体外接球体积的求法,线面角的定义,线面垂直的判定及其性质,考查逻辑推理能力和运算求解能力,属于中档题.
13.【答案】C
【解析】解:集合,
则,
,
则
故选:
根据已知条件,结合交集的定义,即可求解.
本题主要考查交集、补集的运算,属于基础题.
14.【答案】D
【解析】解:设l的倾斜角为,
由题意可得,,,a,,
解得,
,
,
故选:
设l的倾斜角为,由题意可得,,,a,,解得a,b,即可得出结论.
本题考查了双曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.
15.【答案】A
【解析】解:因为三种盖法的屋顶斜面与水平面所成二面角都是,三种盖法的屋顶在水平面上的射影面积都相同,可设为,
由面积射影公式得:,,,
所以
故选:
根据三种盖法的屋顶斜面与水平面所成二面角相等,且屋顶在水平面上的射影面积相等,由面积射影公式即可求得屋顶面积相等.
本题考查了二面角知识在实际生活中的应用问题,由面积射影公式即可得出结论,是基础题.
16.【答案】D
【解析】解:由题意,直线与直线相互垂直,设曲线上的点为,满足,
即,
则当,时,,
当,时,,
当,时,,
当,时,,
所以曲线是以,,,为顶点的矩形,
设曲线上的点为,满足,即,
所以是椭圆,
所以二者公共点的个数只可能是0、4、8个,
故选:
由题意结合点到直线距离公式,整理等式,可判断曲线为矩形,曲线为椭圆,则由图形的对称性即可得到结果.
本题考查直线与曲线交点个数的求法,属于中档题.
17.【答案】解:由题意可得,设的公比为q,,
由,,可得,,
则,解得,,
;
,
则前n项和,
所以当或4时,取得最小值
【解析】由等比数列的通项公式、求和公式可得所求;
由对数的运算性质可得,再由等差数列的求和公式和二次函数的最值可得所求.
本题考查等比数列和等差数列的通项公式、求和公式的运用,以及前n项和的最值,考查方程思想和运算能力,属于基础题.
18.【答案】解:由题意,
解得分
在中,,,
所以分
在中,,,
所以分
分
分
取中点Q,连接OQ,PQ,则,
得或它的补角为异面直线与OP所成的角.分
又,,得,,分
由余弦定理得,分
得异面直线与OP所成的角为分
【解析】由题意圆柱的表面积为,,建立关于圆柱高的方程求出,即得棱锥的高,再由,解出解出AP,进而解出BP,即可解出底面积,再棱锥的体积公式求体积即可;
取中点Q,连接OQ,PQ,可证得或它的补角为异面直线与OP所成的角,在三角形POQ中求异面直线所成的角即可.
本题考查了求三棱锥的体积与求两异面直线所成的角,在圆柱这一背景下,考查这两个问题方式比较新颖,解答本题关键是正确理解这些几何图形之间的位置关系的转化.
19.【答案】由题意可得,,
所以椭圆的标准方程为,离心率为
直线l的方程为,代入椭圆方程得,设,,
则,
,
又点O到直线AB的距离,
,
即的面积为
【解析】根据题意和椭圆的定义可知a,c,再根据,即可求出b,由此即可求出椭圆的方程和离心率;
求出直线l的方程,将其与椭圆方程联立,设,,求出,,根据弦长公式求出的长度,再根据点到直线的距离公式求出点O到直线AB的距离,再根据面积公式即可求出结果.
本题主要考查椭圆方程的求解,椭圆离心率的求解,椭圆中的面积问题,直线与椭圆的位置关系等知识,属于中等题.
20.【答案】解:证明:在四棱锥中,
面ABCD,面ABCD,面ABCD,
,,在直角梯形ABCD中,,,
又面ADP,面ADP,
面ADP,又面ADP,
;
由题意及得,存在一点M,使得直线AM垂直平面PCD,
在四棱锥中,,,
建系如图所示,根据题意可得:
,,,,,
,,,
设,,
又点M在线段CP上,,
,
,,
若面PCD,
则,
解得,
,
;
由题意及可得:,,,
设,
,
,
设,则,
又,,
,
当时,,此时取得最大为,
又在上单调递减,
当最大时,直线CQ与DP所成的角取得最小,
又,,
故所求线段BQ长为
【解析】通过定义法证明线面垂直,即可证出两线垂直;
通过建立空间直角坐标系,表达坐标点,进而根据线面垂直的性质,证明直线AM与和都垂直,求出点M的坐标,进而求出线段AM的长;
通过向量关系表达出,再表达出,列出直线CQ与DP所成的角的表达式,求出最值和最值成立的条件,进而求出线段BQ的长.
本题考查线面垂直的判定定理及性质,向量法求解距离,向量法求解线线角,函数思想,属中档题.
21.【答案】解:设,
由题意,,
而,
由知,,
故
证明:设,,
则,,
故由,得,即,
由于,故,
所以为定值.
由题,设直线OA、OB的斜率分别为k、,
则,,
故直线AB的方程为,
设,则,
所以O到直线AB距离为,
当时,,故,
故原点O到直线AB距离的取值范围为
【解析】根据函数表达式可设,结合两点间距离公式可得,整理即可求解;
设,,则可得到,,由平行关系可得,整理即可证明;
设直线OA、OB的斜率分别为k、,代入函数表达式可得A,B的坐标,即可得到直线AB的表达式,利用点到直线距离公式,进而求解.
本题主要考查平面向量的数量积公式,考查转化能力,属于难题.
2022-2023学年上海市金山中学高二下学期期末数学试题含答案: 这是一份2022-2023学年上海市金山中学高二下学期期末数学试题含答案,共17页。试卷主要包含了填空题,单选题,解答题等内容,欢迎下载使用。
2022-2023学年上海市金山中学、闵行中学、嘉定一中三校高二(下)联考数学试卷(5月份)(含解析): 这是一份2022-2023学年上海市金山中学、闵行中学、嘉定一中三校高二(下)联考数学试卷(5月份)(含解析),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年上海市徐汇中学高二(下)期末数学试卷(含解析): 这是一份2022-2023学年上海市徐汇中学高二(下)期末数学试卷(含解析),共16页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












