
还剩18页未读,
继续阅读
所属成套资源:七年级数学下册压轴题攻略(人教版)
成套系列资料,整套一键下载
第五章 相交线与平行线压轴题考点训练(解析版)-七年级数学下册压轴题攻略(人教版)
展开
这是一份第五章 相交线与平行线压轴题考点训练(解析版)-七年级数学下册压轴题攻略(人教版),共21页。
第五章 相交线与平行线压轴题考点训练
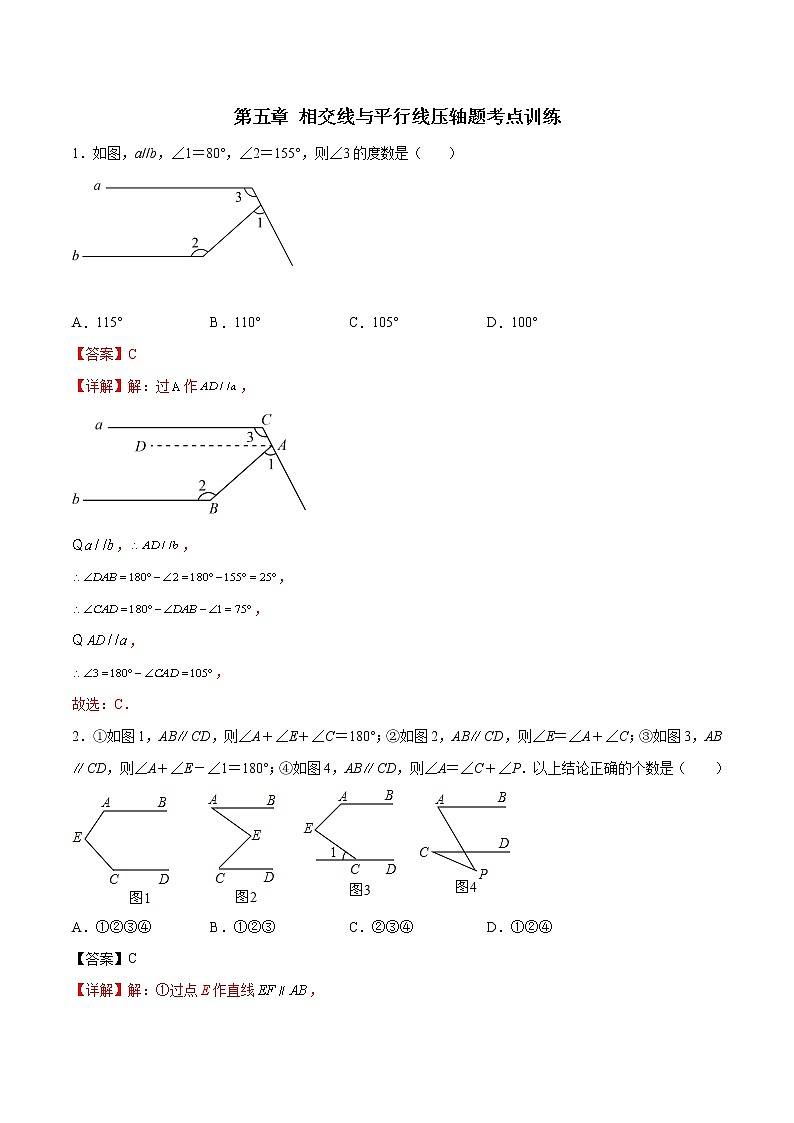
1.如图,a//b,∠1=80°,∠2=155°,则∠3的度数是( )
A.115° B.110° C.105° D.100°
【答案】C
【详解】解:过作,
,,
,
,
,
,
故选:C.
2.①如图1,ABCD,则∠A+∠E+∠C=180°;②如图2,ABCD,则∠E=∠A+∠C;③如图3,ABCD,则∠A+∠E-∠1=180°;④如图4,ABCD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.①②③④ B.①②③ C.②③④ D.①②④
【答案】C
【详解】解:①过点E作直线,
∵,∴,∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,故①错误;
②过点E作直线,
∵,∴,∴∠A=∠1,∠2=∠C,
∴∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故②正确;
③过点E作直线,
∵,∴,∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC-∠2=180°,即∠A+∠AEC-∠1=180°,故③正确;
④如图,过点P作直线,
∵,∴,∴∠1=∠FPA,∠C=∠FPC,
∵∠FPA=∠FPC+∠CPA,∴∠1=∠C+∠CPA,∵AB∥CD,∴∠A=∠1,即∠A=∠C+∠CPA,故④正确.
综上所述,正确的小题有②③④.故选:C.
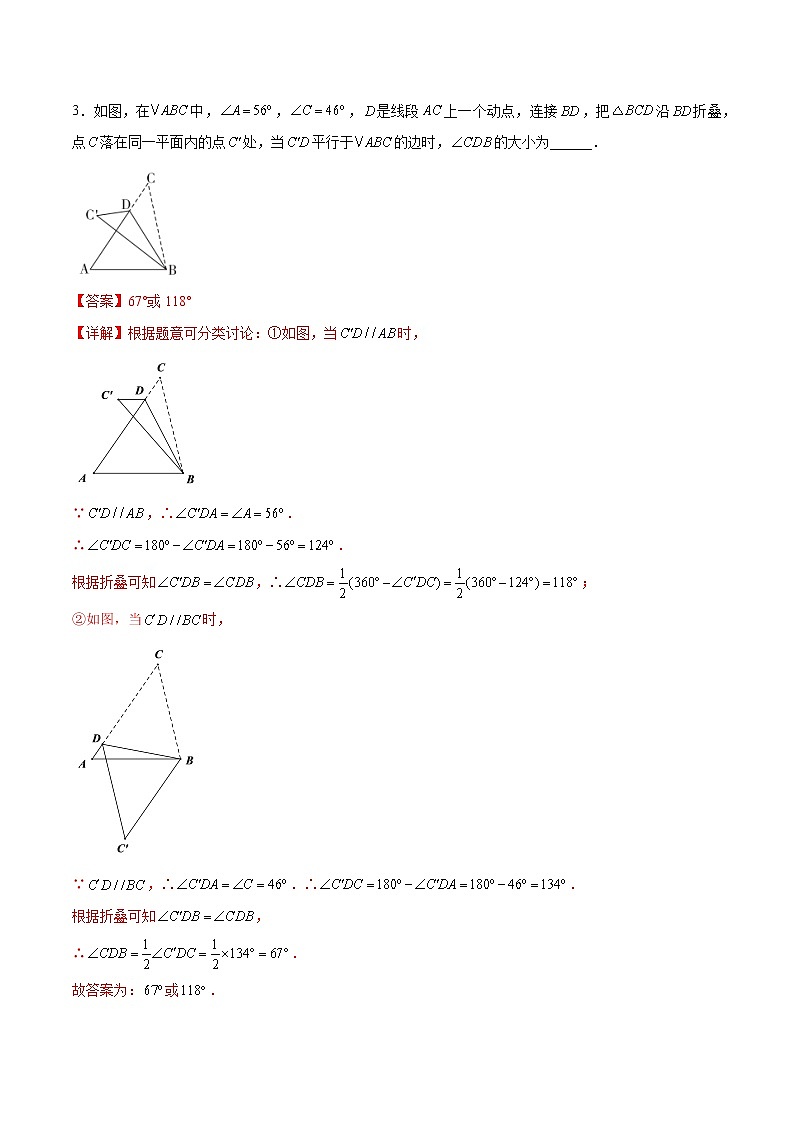
3.如图,在中,,,是线段上一个动点,连接,把沿折叠,点落在同一平面内的点处,当平行于的边时,的大小为______.
【答案】67°或118°
【详解】根据题意可分类讨论:①如图,当时,
∵,∴.
∴.
根据折叠可知,∴;
②如图,当时,
∵,∴.∴.
根据折叠可知,
∴.
故答案为:或.
4.如图,已知,,,则________度.
【答案】110
【详解】过E作一条直线
∵,∴,
∵,,∴,
∴
又∵,∴.
故答案为:110.
5.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACH=______°.
【答案】57
【详解】解:∵BC平分∠ABD,∴∠HBC=∠DBC=,
∵BC⊥AE,DE⊥AE,∴BC∥DE,∴∠3+∠DBC=180°,
∵∠2+∠3=180°,∴∠DBC=∠2,∴CH∥BD,∴∠DBA=∠1=66°,
∴∠DBC=∠2=,∴∠ACH=∠ACB-∠2=90°-33°=57°.
故答案为:57.
6.如图,在Rt△ABC,∠B=90°,∠ACB=50°.将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为_____°.
【答案】100
【详解】解:∵,∴
∴
由旋转的性质可得
∴
∴
故答案为:100.
7.如图,直线分别与直线,交于点A,B,,,若直线,保持不动,将直线绕点A逆时针旋转,使得,则旋转的最小角度是______.
【答案】
【详解】解:过点A作,
∵,∴,
∴.
8.如图,在中,,,点D在BC上,将沿直线AD翻折后,点C落在点E处,连结DE,如果,那么______°.
【答案】70
【详解】解:由翻折性质可得≌,∴,,
∵,∴,
∵,,∴,∴,
∴,
∵,∴,
在中,.
故答案为:70.
9.已知:AB∥CD.点E在CD上,点F,H在AB上,点G在AB,CD之间,连接FG,EH,GE,∠GFB=∠CEH.
(1)如图1,求证:GF∥EH;
(2)如图2,若∠GEH=α,FM平分∠AFG,EM平分∠GEC,试问∠M与α之间有怎样的数量关系(用含α的式子表示∠M)?请写出你的猜想,并加以证明.
【答案】(1)证明见解析过程;(2)∠FME=90°- ,证明见解析过程.
【解析】(1)证明:∵AB∥CD,∴∠CEH=∠EHB,
∵∠GFB=∠CEH,∴∠GFB=∠EHB,∴GF∥EH;
(2)解:∠FME=90°-,理由如下:
如图2,过点M作MQ∥AB,过点G作GP∥AB,
∵AB∥CD,∴MQ∥CD,∴∠AFM=∠FMQ,∠QME=∠MEC,
∴∠FME=∠FMQ+∠QME=∠AFM+∠MEC,
同理,∠FGE=∠FGP+∠PGE=∠AFG+∠GEC,
∵FM平分∠AFG,EM平分∠GEC,
∴∠AFG=2∠AFM,∠GEC=2∠MEC,∴∠FGE=2∠FME,
由(1)知,GF∥EH,∴∠FGE+∠GEH=180°,
∵∠GEH=α,∴∠FGE=180°-α,∴2∠FME=180°-α,∴∠FME=90°-.
10.已知:如图1,直线AB//CD,分别交,于,两点,,的平分线相交于点.
(1)求的度数;
(2)如图2,,的平分线相交于点,请写出与之间的等量关系,并说明理由;
(3)在图2中作,的平分线相交于点,作,的平分线相交于点,依此类推,作,的平分线相交于点,请直接写出的度数.
【答案】(1)90°;(2)∠M1=∠M.证明见解析;(3)()2021×90°
【解析】(1)解:如图1中,
∵AB∥CD,∴∠AEF+∠CFE=180°,
∵∠AEF,∠CFE的平分线相交于点M,∴∠MEF=∠AEF,∠EFM=∠CFE,
∴∠MEF+∠MFE=(∠AEF+∠CFE)=90°,∴∠M=180°-90°=90°;
(2)结论:∠M1=∠M.理由:如图2中,过点M1作M1J∥AB.
∵AB∥CD,M1J∥AB,∴M1J∥CD,
∵∠AEM,∠CFM的平分线相交于点M1,
∴∠AEM1=∠AEM,∠CFM1=∠CFM,
∵∠EM1J=∠AEM1,∠JM1F=∠CFM1
∴∠EM1F=∠AEM1+∠CFM1=(∠AEM+∠CFM)=×90°=45°;所以∠EM1F=∠M.
(3)由(2)可知,∠M1=×90°,
同法可知,∠M2=∠M1=∠M,•••,∠Mn=()n×90°,
当n=2021时,∠M2021=()2021×90°.
11.平面内有直线AB和直线CD,点E是平面内任意一点,连接AE、CE,∠AEC=60°.
(1)若直线AB∥CD;
如图1,当点E在两条平行线之间时,直接写出∠BAE与∠DCE的数量关系 ;
如图2,当点E在两条平行线外部时,直接写出∠BAE与∠DCE的数量关系 ;
(2)若直线AB与CD相交于点O,且∠AOC=60°,如图3,当点E在∠AOC内部,且∠AEC=45°,猜想∠BAE与∠DCE的数量关系,并证明;
(3)我们小学学习过三角形的内角和等于180°,若直线AB与CD相交于点O,且∠AOC=60°,如图4,当点E在∠AOC外部,且∠AEC=45°,分别作射线AM平分∠BAE、作射线CN平分∠DCE,反向延长AM与CN交于点P,求∠APN的度数?
【答案】(1)①∠BAE+∠DCE=60°;②∠DCE﹣∠BAE=60°;(2)∠BAE+∠DCE=105°,见解析;(3)52.5°
【解析】(1)解:①∠BAE+∠DCE=60°,理由如下:
如图1,过点E作EF∥AB,
∴∠BAE=∠AEF,
∵AB//CD,∴EF//CD,∴∠DCE=∠CEF,
∵∠AEC=60°,∴∠BAE+∠DCE=∠AEF+∠CEF=∠AEC=60°;
故答案为:∠BAE+∠DCE=60°.
②∠DCE﹣∠BAE=60°,理由如下:
如图2,过点E作EF//AB,
∴∠BAE=∠AEF,
∵AB//CD,∴EF//CD,∴∠DCE=∠CEF,
∵∠AEC=60°,∴∠DCE﹣∠BAE=∠CEF﹣∠AEF=∠AEC=60°.
故答案为:∠DCE﹣∠BAE=60°.
(2)猜想:∠BAE+∠DCE=105°,理由如下:
如图3,连接OE,
∵∠BAE是△AOE的外角,∠DCE是△COE的外角,∴∠BAE=∠AOE+∠AEO,∠DCE=∠COE+∠CEO,
∵∠AOC=60°,∠AEC=45°,
∴∠BAE+∠DCE=∠AOE+∠AEO+∠COE+∠CEO=∠AOC+∠AEC=60°+45°=105°;
(3)如图4,设AO与CE相交于点G,
设∠AGE=∠CGO=x°,则∠AGC=180°﹣x°,
∵∠BAE是△AEG的外角,∠AEC=45°,∴∠BAE=∠AEC+∠AGE=45°+x°,
∵AM平分∠BAE,∴∠BAM=∠EAM=∠BAE=22.5°+x°,∴∠PAG=∠BAM=22.5°+x°,
∵∠DCE是△COG的外角,∠AOC=60°,∴∠DCE=∠CGO+∠AOC=x°+60°,
∵CN平分∠DCE,∴∠DCN=∠ECN=∠DCE=x°+30°,
∵∠PAG+∠AGC+∠ECN+∠APC=360°,
∴∠APC=360°﹣∠PAG﹣∠AGC﹣∠ECN
=360°﹣(22.5°+x°)﹣(180°﹣x°)﹣(x°+30°)=127.5°,
∴∠APN=180°﹣∠APC=52.5°.
12.已知,如图1,直线,E为直线上方一点,连接,与交于P点.
(1)若,则_________
(2)如图1所示,作的平分线交于点F,点M为上一点,的平分线交于点H,过点H作交的延长线于点G,,且,求的度数.
(3)如图2,在(2)的条件下,,将绕点F顺时针旋转,速度为每秒钟,记旋转中的为,同时绕着点D顺时针旋转,速度为每秒钟,记旋转中的为,当旋转一周时,整个运动停止.设运动时间为t(秒),则当其中一条边与的边DF′互相垂直时,直接写出t的值.
【答案】(1)40;(2)=70°;(3)t的值为10.
【解析】(1)解:∵,,∴∠EPB=∠CDE=70°,
∵∠ABE是△BEP的外角,,∴∠E=∠ABE-∠EPB=110°-70°=40°,
故答案为:40;
(2)解:∵,∴∠GFB=∠FBE,∠HDF=∠PFD
∵FH平分,∴∠GFH=∠HFP,∴∠GFB=2∠HFB=2∠HFD+2∠DFP
∵DF平分,∴∠FDH=∠FDE=∠PFD,∴∠EPB=∠PDH=2∠PDF=2∠PFD
∵∠EBF为△EBP的外角,∴∠EBF=∠E+∠EPB=∠E+2∠PFD,∴2∠HFD+2∠DFP=∠E+2∠PFD,
∴∠E=2∠DFH,
∵,
∴4∠DFH=3∠DFH+20°,∴∠DFH=20°,
∵,∴∠FHG=90°,∴∠G+∠GFH=90°,
∴∠G+∠PFH=∠G+∠HFD+∠PFD=90°,
∴∠G+∠PFD=90°-∠HFD=90°-20°-70°,∴=70°;
(3)当时,∠HFP=∠HFD+∠DFP=45°,∴∠GFH=∠HFP=45°,∴∠G=45°,
当其中一条边与的边DF′互相垂直,分三种情况,
当G′H′⊥DF′时,FH′交CD与S,FH′∥F′D,∠FSC=∠CDF′,∠CDF′=25°+5t,∠FSC=45°+3°t,
∴25°+5t =45°+3°t,解得t=10,
当GF⊥F′D时,GF交CD于R,交DF′于Q,∠HDF′=25°+5t,∠CRG=∠GFA=3t-90°,
∠QRD+∠QDR=90°即3t-90°+180°-(25+5t)=90°,解得t=-12.5<0舍去,
当H′F⊥DF′,H′F交CD于U,交DF′于V,∠HDF′=25°+5°t,∠CUF=∠AFH′=3°t-90°-45°,
∵∠VUD+∠UDV=90°, ∴180°-(25°+5°t)+3°t-90°-45°=90°,解得t=-35<0舍去,
综合t的值为10.
13.如图①.已知,点为平面内一点,于点,过点作于点,设.
(1)若,求的度数;
(2)如图②,若点、在上,连接、、,使得平分、平分,求的度数;
(3)如图③,在(2)问的条件下,若平分,且,求的度数.
【答案】(1)30°;(2)45°;(3)97.5°
【详解】解:(1)延长,交于点,如图,
,,..
,.
,.
;
(2)延长,交于点,如图,
,,..
,.
,..
平分,.
,.
平分,.
;
(3),.
平分,.
,.
,.
.
由(2)知:.
,..
.解得:.
..
14.已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,求∠GMH的度数.
【答案】(1)见详解;(2)∠MEB=40°,(3)∠GMH=80°
【详解】(1)证明:∵∠ABU+∠ABD=180°,∠ABU+∠CDV=180°.
∴∠ABU=180°-∠ABD,∠CDV=180°-∠ABU,∴∠ABD=∠CDV,∴AB∥CD;
(2)解:∵AB∥CD;∴∠ABD=∠RDB,∴∠ABE+∠EBD=∠FDB+∠FDR,
∵BE∥DF,∴∠EBD=∠FDB,∴∠ABE=∠FDR,
∵∠FDR=35°,∴∠ABE=∠FDR=35°,∴∠MEB=∠ABE+5°=35°+5°=40°,
(3)解:设ME交AB于S,∵MG∥EN,∴∠NES=∠GMS=∠GES,设∠NES=y°,
∵∠EBD=2∠NEG∴∠NEG=∠NES+∠GES=2∠NES=2y°,∴∠EBD =4∠NES=4y°,
∵∠EDC=∠CDB,
设∠EDC=x°,∴∠CDB=7x°,
∵AB∥CD,∴∠ABD+∠CDB=180°,即∠GBE+∠EBD+∠CDB=180°,∴35+4y+7x=180,
∵∠BDE=∠BDC-∠EDC=7x-x=6x,∴∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,
∵EB平分∠DEN,∴∠NEB=∠BED,
∵∠NEB=∠NES+∠SEB=y°+40°,∴y°+40°=180°-4y°-6x°,∴,解得,
∴∠EBD=4y°=40°=∠MEB,∴ME∥UV,
∵MH⊥UV,∴MH⊥ME,∴∠SMH=90°,,
∵∠SMG=∠NES=10°,∴∠GMH=90°-∠SMG=90°-10°=80°.
15.已知AMCN,点B为平面内一点,于B.
(1)如图1,直接写出和之间的数量关系.
(2)如图2,过点B作于点D,求证:.
(3)如图3,在(2)问的条件下,点E、F在上,连接、、,平分,平分,若,求的度数.
【答案】(1);(2)见解析;(3)
【解析】(1)解:如图,
,,
,,;
(2)解:如图,
过点作,,,即,
又,,
,,,,;
(3)解:如图,
过点B作,平分,平分,,,
由(2)可得,,
设,,
则,,,,,
,,,可得
,①
由可得,②
由①②联立方程组,解得,,
.
16.已知,点、分别是、上的点,点在、之间,连接、.
(1)如图1,若,求的度数.
(2)在(1)的条件下,分别作和的平分线交于点,求的度数.
(3)如图2,若点是下方一点,平分,平分,已知.则判断以下两个结论是否正确,并证明你认为正确的结论.①为定值;②为定值.
【答案】(1) (2) (3)②是正确的,证明见解析
【详解】(1)如图所示,过点作,
∵,,∴,
∴,,∴,
∵,∴,∴.
(2)如图所示,过点作,过点作,
∵,∴,
∴,,∴,
∵,∴,
∵平分,平分,∴,,
∴,
∵,∴,,
∴.
(3)如图所示,∵,∴,
∵平分,∴,∴,∴,
∵平分,∴,
设,则,
∴,
∴,,
∴②中的值为定值.
故②是正确的.
第五章 相交线与平行线压轴题考点训练
1.如图,a//b,∠1=80°,∠2=155°,则∠3的度数是( )
A.115° B.110° C.105° D.100°
【答案】C
【详解】解:过作,
,,
,
,
,
,
故选:C.
2.①如图1,ABCD,则∠A+∠E+∠C=180°;②如图2,ABCD,则∠E=∠A+∠C;③如图3,ABCD,则∠A+∠E-∠1=180°;④如图4,ABCD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.①②③④ B.①②③ C.②③④ D.①②④
【答案】C
【详解】解:①过点E作直线,
∵,∴,∴∠A+∠1=180°,∠2+∠C=180°,
∴∠A+∠C+∠AEC=360°,故①错误;
②过点E作直线,
∵,∴,∴∠A=∠1,∠2=∠C,
∴∠AEC=∠A+∠C,即∠AEC=∠A+∠C,故②正确;
③过点E作直线,
∵,∴,∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC-∠2=180°,即∠A+∠AEC-∠1=180°,故③正确;
④如图,过点P作直线,
∵,∴,∴∠1=∠FPA,∠C=∠FPC,
∵∠FPA=∠FPC+∠CPA,∴∠1=∠C+∠CPA,∵AB∥CD,∴∠A=∠1,即∠A=∠C+∠CPA,故④正确.
综上所述,正确的小题有②③④.故选:C.
3.如图,在中,,,是线段上一个动点,连接,把沿折叠,点落在同一平面内的点处,当平行于的边时,的大小为______.
【答案】67°或118°
【详解】根据题意可分类讨论:①如图,当时,
∵,∴.
∴.
根据折叠可知,∴;
②如图,当时,
∵,∴.∴.
根据折叠可知,
∴.
故答案为:或.
4.如图,已知,,,则________度.
【答案】110
【详解】过E作一条直线
∵,∴,
∵,,∴,
∴
又∵,∴.
故答案为:110.
5.如图,已知BC⊥AE,DE⊥AE,∠2+∠3=180°.若∠1=66°,BC平分∠ABD,则∠ACH=______°.
【答案】57
【详解】解:∵BC平分∠ABD,∴∠HBC=∠DBC=,
∵BC⊥AE,DE⊥AE,∴BC∥DE,∴∠3+∠DBC=180°,
∵∠2+∠3=180°,∴∠DBC=∠2,∴CH∥BD,∴∠DBA=∠1=66°,
∴∠DBC=∠2=,∴∠ACH=∠ACB-∠2=90°-33°=57°.
故答案为:57.
6.如图,在Rt△ABC,∠B=90°,∠ACB=50°.将Rt△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,连接CC′.若AB∥CC′,则旋转角的度数为_____°.
【答案】100
【详解】解:∵,∴
∴
由旋转的性质可得
∴
∴
故答案为:100.
7.如图,直线分别与直线,交于点A,B,,,若直线,保持不动,将直线绕点A逆时针旋转,使得,则旋转的最小角度是______.
【答案】
【详解】解:过点A作,
∵,∴,
∴.
8.如图,在中,,,点D在BC上,将沿直线AD翻折后,点C落在点E处,连结DE,如果,那么______°.
【答案】70
【详解】解:由翻折性质可得≌,∴,,
∵,∴,
∵,,∴,∴,
∴,
∵,∴,
在中,.
故答案为:70.
9.已知:AB∥CD.点E在CD上,点F,H在AB上,点G在AB,CD之间,连接FG,EH,GE,∠GFB=∠CEH.
(1)如图1,求证:GF∥EH;
(2)如图2,若∠GEH=α,FM平分∠AFG,EM平分∠GEC,试问∠M与α之间有怎样的数量关系(用含α的式子表示∠M)?请写出你的猜想,并加以证明.
【答案】(1)证明见解析过程;(2)∠FME=90°- ,证明见解析过程.
【解析】(1)证明:∵AB∥CD,∴∠CEH=∠EHB,
∵∠GFB=∠CEH,∴∠GFB=∠EHB,∴GF∥EH;
(2)解:∠FME=90°-,理由如下:
如图2,过点M作MQ∥AB,过点G作GP∥AB,
∵AB∥CD,∴MQ∥CD,∴∠AFM=∠FMQ,∠QME=∠MEC,
∴∠FME=∠FMQ+∠QME=∠AFM+∠MEC,
同理,∠FGE=∠FGP+∠PGE=∠AFG+∠GEC,
∵FM平分∠AFG,EM平分∠GEC,
∴∠AFG=2∠AFM,∠GEC=2∠MEC,∴∠FGE=2∠FME,
由(1)知,GF∥EH,∴∠FGE+∠GEH=180°,
∵∠GEH=α,∴∠FGE=180°-α,∴2∠FME=180°-α,∴∠FME=90°-.
10.已知:如图1,直线AB//CD,分别交,于,两点,,的平分线相交于点.
(1)求的度数;
(2)如图2,,的平分线相交于点,请写出与之间的等量关系,并说明理由;
(3)在图2中作,的平分线相交于点,作,的平分线相交于点,依此类推,作,的平分线相交于点,请直接写出的度数.
【答案】(1)90°;(2)∠M1=∠M.证明见解析;(3)()2021×90°
【解析】(1)解:如图1中,
∵AB∥CD,∴∠AEF+∠CFE=180°,
∵∠AEF,∠CFE的平分线相交于点M,∴∠MEF=∠AEF,∠EFM=∠CFE,
∴∠MEF+∠MFE=(∠AEF+∠CFE)=90°,∴∠M=180°-90°=90°;
(2)结论:∠M1=∠M.理由:如图2中,过点M1作M1J∥AB.
∵AB∥CD,M1J∥AB,∴M1J∥CD,
∵∠AEM,∠CFM的平分线相交于点M1,
∴∠AEM1=∠AEM,∠CFM1=∠CFM,
∵∠EM1J=∠AEM1,∠JM1F=∠CFM1
∴∠EM1F=∠AEM1+∠CFM1=(∠AEM+∠CFM)=×90°=45°;所以∠EM1F=∠M.
(3)由(2)可知,∠M1=×90°,
同法可知,∠M2=∠M1=∠M,•••,∠Mn=()n×90°,
当n=2021时,∠M2021=()2021×90°.
11.平面内有直线AB和直线CD,点E是平面内任意一点,连接AE、CE,∠AEC=60°.
(1)若直线AB∥CD;
如图1,当点E在两条平行线之间时,直接写出∠BAE与∠DCE的数量关系 ;
如图2,当点E在两条平行线外部时,直接写出∠BAE与∠DCE的数量关系 ;
(2)若直线AB与CD相交于点O,且∠AOC=60°,如图3,当点E在∠AOC内部,且∠AEC=45°,猜想∠BAE与∠DCE的数量关系,并证明;
(3)我们小学学习过三角形的内角和等于180°,若直线AB与CD相交于点O,且∠AOC=60°,如图4,当点E在∠AOC外部,且∠AEC=45°,分别作射线AM平分∠BAE、作射线CN平分∠DCE,反向延长AM与CN交于点P,求∠APN的度数?
【答案】(1)①∠BAE+∠DCE=60°;②∠DCE﹣∠BAE=60°;(2)∠BAE+∠DCE=105°,见解析;(3)52.5°
【解析】(1)解:①∠BAE+∠DCE=60°,理由如下:
如图1,过点E作EF∥AB,
∴∠BAE=∠AEF,
∵AB//CD,∴EF//CD,∴∠DCE=∠CEF,
∵∠AEC=60°,∴∠BAE+∠DCE=∠AEF+∠CEF=∠AEC=60°;
故答案为:∠BAE+∠DCE=60°.
②∠DCE﹣∠BAE=60°,理由如下:
如图2,过点E作EF//AB,
∴∠BAE=∠AEF,
∵AB//CD,∴EF//CD,∴∠DCE=∠CEF,
∵∠AEC=60°,∴∠DCE﹣∠BAE=∠CEF﹣∠AEF=∠AEC=60°.
故答案为:∠DCE﹣∠BAE=60°.
(2)猜想:∠BAE+∠DCE=105°,理由如下:
如图3,连接OE,
∵∠BAE是△AOE的外角,∠DCE是△COE的外角,∴∠BAE=∠AOE+∠AEO,∠DCE=∠COE+∠CEO,
∵∠AOC=60°,∠AEC=45°,
∴∠BAE+∠DCE=∠AOE+∠AEO+∠COE+∠CEO=∠AOC+∠AEC=60°+45°=105°;
(3)如图4,设AO与CE相交于点G,
设∠AGE=∠CGO=x°,则∠AGC=180°﹣x°,
∵∠BAE是△AEG的外角,∠AEC=45°,∴∠BAE=∠AEC+∠AGE=45°+x°,
∵AM平分∠BAE,∴∠BAM=∠EAM=∠BAE=22.5°+x°,∴∠PAG=∠BAM=22.5°+x°,
∵∠DCE是△COG的外角,∠AOC=60°,∴∠DCE=∠CGO+∠AOC=x°+60°,
∵CN平分∠DCE,∴∠DCN=∠ECN=∠DCE=x°+30°,
∵∠PAG+∠AGC+∠ECN+∠APC=360°,
∴∠APC=360°﹣∠PAG﹣∠AGC﹣∠ECN
=360°﹣(22.5°+x°)﹣(180°﹣x°)﹣(x°+30°)=127.5°,
∴∠APN=180°﹣∠APC=52.5°.
12.已知,如图1,直线,E为直线上方一点,连接,与交于P点.
(1)若,则_________
(2)如图1所示,作的平分线交于点F,点M为上一点,的平分线交于点H,过点H作交的延长线于点G,,且,求的度数.
(3)如图2,在(2)的条件下,,将绕点F顺时针旋转,速度为每秒钟,记旋转中的为,同时绕着点D顺时针旋转,速度为每秒钟,记旋转中的为,当旋转一周时,整个运动停止.设运动时间为t(秒),则当其中一条边与的边DF′互相垂直时,直接写出t的值.
【答案】(1)40;(2)=70°;(3)t的值为10.
【解析】(1)解:∵,,∴∠EPB=∠CDE=70°,
∵∠ABE是△BEP的外角,,∴∠E=∠ABE-∠EPB=110°-70°=40°,
故答案为:40;
(2)解:∵,∴∠GFB=∠FBE,∠HDF=∠PFD
∵FH平分,∴∠GFH=∠HFP,∴∠GFB=2∠HFB=2∠HFD+2∠DFP
∵DF平分,∴∠FDH=∠FDE=∠PFD,∴∠EPB=∠PDH=2∠PDF=2∠PFD
∵∠EBF为△EBP的外角,∴∠EBF=∠E+∠EPB=∠E+2∠PFD,∴2∠HFD+2∠DFP=∠E+2∠PFD,
∴∠E=2∠DFH,
∵,
∴4∠DFH=3∠DFH+20°,∴∠DFH=20°,
∵,∴∠FHG=90°,∴∠G+∠GFH=90°,
∴∠G+∠PFH=∠G+∠HFD+∠PFD=90°,
∴∠G+∠PFD=90°-∠HFD=90°-20°-70°,∴=70°;
(3)当时,∠HFP=∠HFD+∠DFP=45°,∴∠GFH=∠HFP=45°,∴∠G=45°,
当其中一条边与的边DF′互相垂直,分三种情况,
当G′H′⊥DF′时,FH′交CD与S,FH′∥F′D,∠FSC=∠CDF′,∠CDF′=25°+5t,∠FSC=45°+3°t,
∴25°+5t =45°+3°t,解得t=10,
当GF⊥F′D时,GF交CD于R,交DF′于Q,∠HDF′=25°+5t,∠CRG=∠GFA=3t-90°,
∠QRD+∠QDR=90°即3t-90°+180°-(25+5t)=90°,解得t=-12.5<0舍去,
当H′F⊥DF′,H′F交CD于U,交DF′于V,∠HDF′=25°+5°t,∠CUF=∠AFH′=3°t-90°-45°,
∵∠VUD+∠UDV=90°, ∴180°-(25°+5°t)+3°t-90°-45°=90°,解得t=-35<0舍去,
综合t的值为10.
13.如图①.已知,点为平面内一点,于点,过点作于点,设.
(1)若,求的度数;
(2)如图②,若点、在上,连接、、,使得平分、平分,求的度数;
(3)如图③,在(2)问的条件下,若平分,且,求的度数.
【答案】(1)30°;(2)45°;(3)97.5°
【详解】解:(1)延长,交于点,如图,
,,..
,.
,.
;
(2)延长,交于点,如图,
,,..
,.
,..
平分,.
,.
平分,.
;
(3),.
平分,.
,.
,.
.
由(2)知:.
,..
.解得:.
..
14.已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.
(1)如图1,求证:AB∥CD;
(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;
(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=∠CDB,求∠GMH的度数.
【答案】(1)见详解;(2)∠MEB=40°,(3)∠GMH=80°
【详解】(1)证明:∵∠ABU+∠ABD=180°,∠ABU+∠CDV=180°.
∴∠ABU=180°-∠ABD,∠CDV=180°-∠ABU,∴∠ABD=∠CDV,∴AB∥CD;
(2)解:∵AB∥CD;∴∠ABD=∠RDB,∴∠ABE+∠EBD=∠FDB+∠FDR,
∵BE∥DF,∴∠EBD=∠FDB,∴∠ABE=∠FDR,
∵∠FDR=35°,∴∠ABE=∠FDR=35°,∴∠MEB=∠ABE+5°=35°+5°=40°,
(3)解:设ME交AB于S,∵MG∥EN,∴∠NES=∠GMS=∠GES,设∠NES=y°,
∵∠EBD=2∠NEG∴∠NEG=∠NES+∠GES=2∠NES=2y°,∴∠EBD =4∠NES=4y°,
∵∠EDC=∠CDB,
设∠EDC=x°,∴∠CDB=7x°,
∵AB∥CD,∴∠ABD+∠CDB=180°,即∠GBE+∠EBD+∠CDB=180°,∴35+4y+7x=180,
∵∠BDE=∠BDC-∠EDC=7x-x=6x,∴∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,
∵EB平分∠DEN,∴∠NEB=∠BED,
∵∠NEB=∠NES+∠SEB=y°+40°,∴y°+40°=180°-4y°-6x°,∴,解得,
∴∠EBD=4y°=40°=∠MEB,∴ME∥UV,
∵MH⊥UV,∴MH⊥ME,∴∠SMH=90°,,
∵∠SMG=∠NES=10°,∴∠GMH=90°-∠SMG=90°-10°=80°.
15.已知AMCN,点B为平面内一点,于B.
(1)如图1,直接写出和之间的数量关系.
(2)如图2,过点B作于点D,求证:.
(3)如图3,在(2)问的条件下,点E、F在上,连接、、,平分,平分,若,求的度数.
【答案】(1);(2)见解析;(3)
【解析】(1)解:如图,
,,
,,;
(2)解:如图,
过点作,,,即,
又,,
,,,,;
(3)解:如图,
过点B作,平分,平分,,,
由(2)可得,,
设,,
则,,,,,
,,,可得
,①
由可得,②
由①②联立方程组,解得,,
.
16.已知,点、分别是、上的点,点在、之间,连接、.
(1)如图1,若,求的度数.
(2)在(1)的条件下,分别作和的平分线交于点,求的度数.
(3)如图2,若点是下方一点,平分,平分,已知.则判断以下两个结论是否正确,并证明你认为正确的结论.①为定值;②为定值.
【答案】(1) (2) (3)②是正确的,证明见解析
【详解】(1)如图所示,过点作,
∵,,∴,
∴,,∴,
∵,∴,∴.
(2)如图所示,过点作,过点作,
∵,∴,
∴,,∴,
∵,∴,
∵平分,平分,∴,,
∴,
∵,∴,,
∴.
(3)如图所示,∵,∴,
∵平分,∴,∴,∴,
∵平分,∴,
设,则,
∴,
∴,,
∴②中的值为定值.
故②是正确的.
相关资料
更多









