

初中数学中考复习 专题2 分类讨论思想
展开专题2 分类讨论思想
一、选择题
1.等腰三角形有一个角的度数为50°,那么它的底角的度数为( D )
A.50° B.65
C.80° D.50°或65°
2.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( D )
A.30° B.60°
C.30°或150° D.60°或120°
3.若直角三角形的两边长分别为3 cm和4 cm,则第三边长为( C )
A.5 cm B. cm
C.5 cm或 cm D.5 cm或7 cm
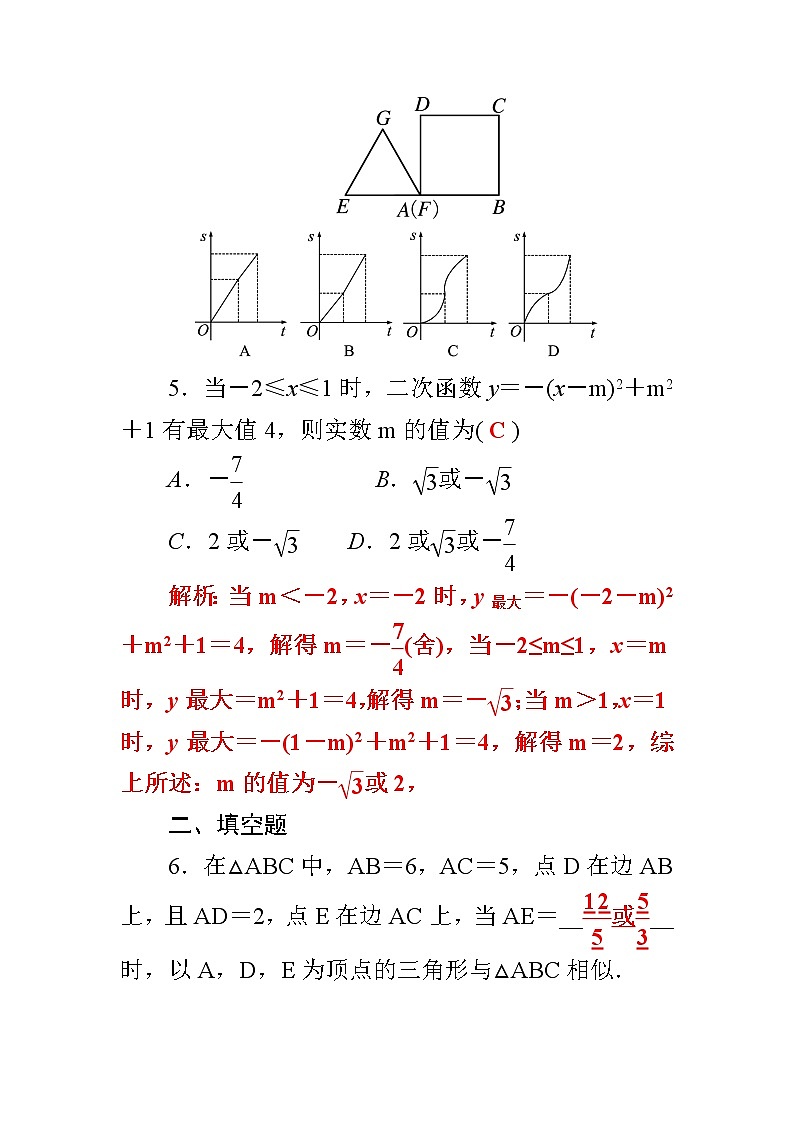
4.(2019·达州)如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( C )
5.当-2≤x≤1时,二次函数y=-(x-m)2+m2+1有最大值4,则实数m的值为( C )
A.- B.或-
C.2或- D.2或或-
解析:当m<-2,x=-2时,y最大=-(-2-m)2+m2+1=4,解得m=-(舍),当-2≤m≤1,x=m时,y最大=m2+1=4,解得m=-;当m>1,x=1时,y最大=-(1-m)2+m2+1=4,解得m=2,综上所述:m的值为-或2,
二、填空题
6.在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=__或__时,以A,D,E为顶点的三角形与△ABC相似.
7.某超市推出如下优惠方案:
(1)一次性购物不超过100元不享受优惠;
(2)一次性购物超过100元但不超过300元一律9折;
(3)一次性购物超过300元一律8折.
小李两次购物分别付款80元,252元,如果他一次性购买以上两次相同的商品,应付款__316或288__元.
8.如图,直线y=-x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是__(-,0)或(-,0)__.
解析:A(-4,0),B(0.-3),∴OA=4,OB=3,∴AB=5,设⊙P与直线AB相切于D,连接PD,则PD⊥AB,PD=1,可证△APD∽△ABO,
∴=,∴=,∴AP=,
∴OP=或OP=,∴P(-,0)或P(-,0).
三、解答题
9.如果四个整数中的三个数分别是2,4,6,且它们的中位数也是整数,求它们的中位数.
解:设第四个数为x,所以对x进行分类讨论:当x≤2时,这组数据按从小到大的顺序排列后为x,2,4,6,这时它的中位数为=3;当2<x<4时,这组数据按从小到大的顺序排列后为2,x,4,6,这时它的中位数为且为整数,所以x不存在;当4≤x<6时,这组数据按从小到大的顺序排列后为2,4,x,6,这时它的中位数为,当x=4时,符合题意;当x≥6时,这组数据按从小到大的顺序排列后为2,4,6,x,这时它的中位数为=5;综上所述,所求的中位数为3或4或5.
10.我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.
(1)求a的值,某户居民上月用水8吨,应收水费多少元;
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
解:(1)a=15÷10=1.5.用8吨水应收水费8×1.5=12(元).
(2)当x>10时,y=2x-5,b=2;
(3)∵假设甲乙用水量均不超过10吨,水费不超过30元,不符合题意;假设乙用水10吨,则甲用水14吨,∴水费是:1.5×10+1.5×10+2×4<46,不符合题意;∴甲、乙两家上月用水均超过10吨.设甲、乙两家上月用水分别为x吨,y吨,则甲用水的水费是(2x-5)元,乙用水的水费是(2y-5)元,则解得:故居民甲上月用水16吨,居民乙上月用水12吨.
11.如图,公交车行驶在笔直的公路上,这条路上有A,B,C,D四个站点,每相邻两站之间的距离为5千米,从A站开往D站的车称为上行车,从D站开往A站的车称为下行车,第一班上行车、下行车分别从A站、D站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在A,D站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
(1)问第一班上行车到B站、第一班下行车到C站分别用时多少?
(2)若第一班上行车行驶时间为t小时,第一班上行车与第一班下行车之间的距离为s千米,求s与t的函数关系式;
(3)一乘客前往A站办事,他在B,C两站间的P处(不含B,C站),刚好遇到上行车,BP=x千米,此时,接到通知,必须在35分钟内赶到,他可选择走到B站或走到C站乘下行车前往A站.若乘客的步行速度是5千米/小时,求x满足的条件.
解:(1)第一班上行车到B站用时=小时,第一班下行车到C站用时=小时;
(2)当0≤t≤时,s=15-60t,当<t≤时,s=60t-15;
(3)由(2)可知同时出发的一对上、下行车的位置关于BC中点对称,设乘客到达A站总时间为t分钟,
①当x=2.5时,往B站用时30分钟,还需要再等下行车5分钟,t=30+5+10=45,不合题意;
②当x<2.5时,只能往B站乘下行车,他离B站x千米,则离他右边最近的下行车离C站也是x千米,这辆下行车离B站(5-x)千米,如果能乘上右侧的第一辆下行车,则≤,解得:x≤,∴0<x≤,∵18≤t<20,∴0<x≤符合题意;如果乘不上右侧第一辆下行车,只能乘右侧第二辆下行车,x>,≤,解得:x≤,∴<x≤,22≤t<28,∴<x≤符合题意;如果乘不上右侧第二辆下行车,只能乘右侧第三辆下行车,x>,≤,解得:x≤,∴<x≤,35≤t<37,不合题意,∴综上,得0<x≤;
③当x>2.5时,乘客需往C站乘坐下行车.离他左边最近的下行车离B站是(5-x)千米,离他右边最近的下行车离C站也是(5-x)千米.如果乘上右侧第一辆下行车,则≤,解得:x≥5,不合题意.∴x≥5,不合题意.如果乘不上右侧第一辆下行车,只能乘右侧第二辆下行车,x<5,≤,解得x≥4,∴4≤x<5,30<t≤32,∴4≤x<5符合题意.如果乘不上右侧第二辆下行车,只能乘右侧第三辆下行车,x<4,≤,解得x≥3,∴3≤x<4,42<t≤44,∴3≤x<4不合题意.综上,得4≤x<5.综上所述,0<x≤或4≤x<5.
中考数学二轮复习考点解读过关练习专题2 分类讨论思想 (教师版): 这是一份中考数学二轮复习考点解读过关练习专题2 分类讨论思想 (教师版),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
中考数学专题复习 专题46 中考数学分类讨论思想: 这是一份中考数学专题复习 专题46 中考数学分类讨论思想,文件包含中考数学专题复习专题46中考数学分类讨论思想教师版含解析docx、中考数学专题复习专题46中考数学分类讨论思想学生版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
初中数学中考复习 专题46 中考数学分类讨论思想(原卷版): 这是一份初中数学中考复习 专题46 中考数学分类讨论思想(原卷版),共6页。试卷主要包含了分类讨论思想含义,分类讨论一般应遵循以下原则,初中数学涉及分类讨论的常见问题等内容,欢迎下载使用。












