初中数学中考复习 专题03 图形的变化（解析版）

这是一份初中数学中考复习 专题03 图形的变化（解析版），共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
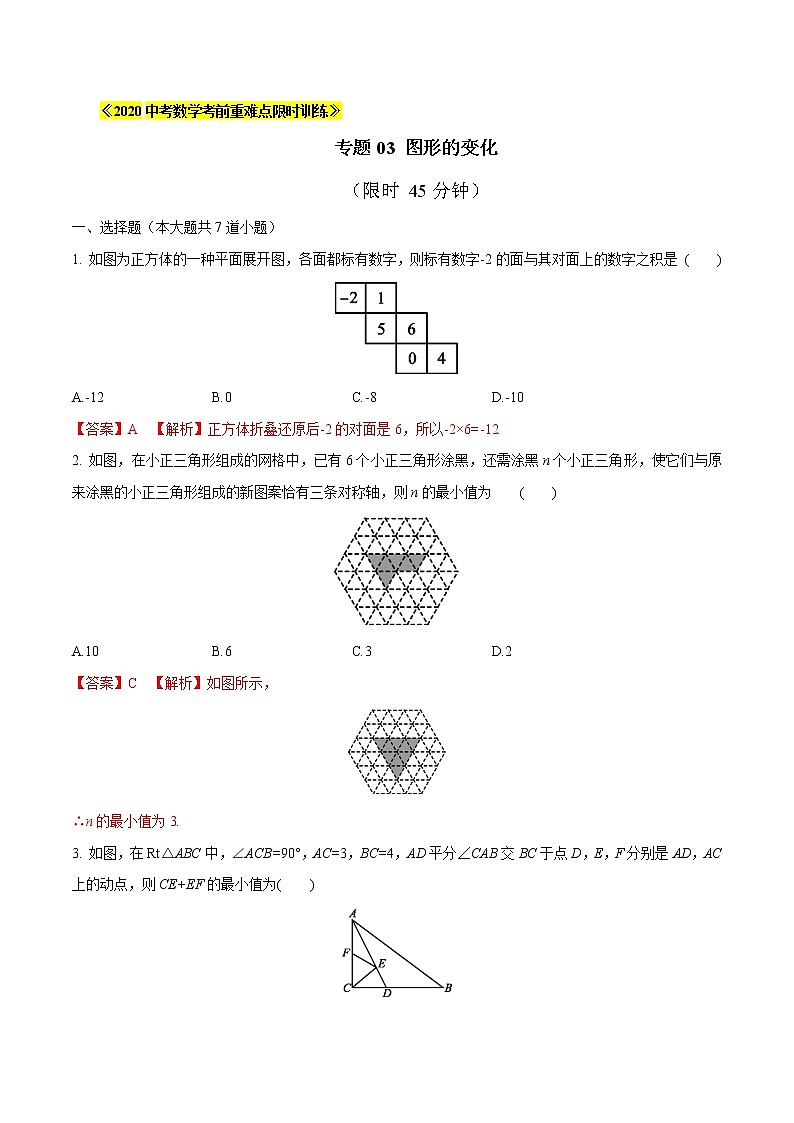
《2020中考数学考前重难点限时训练》专题03 图形的变化（限时 45分钟）一、选择题（本大题共7道小题）1. 如图为正方体的一种平面展开图，各面都标有数字，则标有数字-2的面与其对面上的数字之积是 (　　)A.-12    B.0     C.-8     D.-10【答案】A　【解析】正方体折叠还原后-2的对面是6，所以-2×6=-12.2. 如图，在小正三角形组成的网格中，已有6个小正三角形涂黑，还需涂黑n个小正三角形，使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴，则n的最小值为              (　　)A.10     B.6     C.3     D.2
【答案】C　【解析】如图所示，∴n的最小值为3.
3. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，AD平分∠CAB交BC于点D，E，F分别是AD，AC上的动点，则CE+EF的最小值为(　　)A.     B.     C.3     D.
【答案】D　【解析】在AB上取一点G，使AG=AF，又∵∠CAD=∠BAD，AE=AE，∴△AEF≌△AEG(SAS)，∴FE=EG，∴CE+EF=CE+EG，∴当C，E，G三点共线，且CG垂直AB时，CE+EF的值最小，最小值为.
4. 一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆，根据图中所示数据，可求这个物体的表面积为              (　　)A.π     B.2π     C.3π     D.(+1)π
【答案】C　【解析】由三视图可知:该几何体是一个圆锥，其轴截面是一个高为的正三角形.∴正三角形的边长==2.∴圆锥的底面圆半径是1，母线长是2，∴底面周长为2π，∴侧面积为×2π×2=2π，，∵底面积为πr2=π，∴全面积是3π.故选C.
5. 如图，在Rt△ABC中，∠BAC=90°，∠B=36°，AD是斜边BC上的中线，将△ACD沿AD对折，使点C落在点F处，线段DF与AB相交于点E，则∠BED等于              (　　)A.120°    B.108°    C.72°    D.36°
【答案】B　【解析】∵在Rt△ABC中，∠BAC=90°，∠B=36°，∴∠C=90°-∠B=54°.∵AD是斜边BC上的中线，∴AD=BD=CD，∴∠BAD=∠B=36°，∠DAC=∠C=54°，∴∠ADC=180°-∠DAC-C=72°.∵将△ACD沿AD对折，使点C落在点F处，∴∠ADF=∠ADC=72°，∴∠BED=∠BAD+∠ADF=36°+72°=108°.故选B.
6. 如图，将△ABC沿BC方向平移1 cm得到△DEF，若△ABC的周长为8 cm，则四边形ABFD的周长为 (　　)A.8 cm         B.9 cm C.10 cm         D.11 cm
【答案】C　【解析】将周长为8 cm的△ABC沿BC方向平移1 cm得到△DEF，∴AD=CF=1 cm，DF=AC.∵AB+BC+AC=8 cm，∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10 cm.
7. 如图，∠AOB=60°，点P是∠AOB内的定点且OP=，若点M，N分别是射线OA，OB上异于点O的动点，则△PMN周长的最小值是              (　　)A.    B.    C.6     D.3
【答案】D　【解析】分别以OB，OA为对称轴作点P的对称点P1，P2，连接OP1，OP2，P1P2，P1P2交射线OA，OB于点M，N，则此时△PMN的周长有最小值，△PMN的周长=PN+PM+MN=P1N+P2M+MN=P1P2，根据轴对称的性质可知OP1=OP2=OP=，∠P1OP2=120°，∴∠OP1M=30°，过点O作MN的垂线段，垂足为Q，在Rt△OP1Q中，可知P1Q=，所以P1P2=2P1Q=3，故△PMN周长的最小值为3.
二、填空题（本大题共6道小题）8. 将一张矩形纸片折叠成如图所示的图形，若AB=10 cm，则AC=　　　　cm. 
【答案】10　【解析】如图，∵矩形的对边平行，∴∠1=∠ACB，由翻折变换的性质，得∠1=∠ABC，∴∠ABC=∠ACB，∴AC=AB，∵AB=10 cm，∴AC=10 cm.故答案为10.
9. 在如图所示的方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A'B'C'，各顶点仍在格点上，则其旋转角的度数是　　　　. 
【答案】90°　【解析】找到一组对应点A，A'，分别与旋转中心连接起来，则∠AOA'为旋转角，为90°.
10. 如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影部分和空白部分.当菱形的两条对角线的长分别为6和8时，阴影部分的面积为　　　　. 
【答案】12　【解析】∵菱形的两条对角线的长分别为6和8，∴菱形的面积=×6×8=24.∵点O是菱形两条对角线的交点，∴阴影部分的面积=×24=12.
11. 如图，在正方形网格中，格点△ABC绕某点顺时针旋转角α(0<α<180°)得到格点△A1B1C1，点A与点A1，点B与点B1，点C与点C1是对应点，则α=　　　　. 
【答案】90°　【解析】∵旋转图形的旋转中心到对应点的距离相等，∴分别作线段AA1，CC1的垂直平分线，两直线相交于点D，则点D即为旋转中心，连接AD，A1D，则α=∠ADA1=90°.
12. 如图，有一张矩形纸片ABCD，AB=8，AD=6，先将矩形纸片ABCD折叠，使边AD落在边AB上，点D落在点E处，折痕为AF;再将△AEF沿EF翻折，AF与BC相交于点G，则△GCF的周长为　　　　. 
【答案】4+2　【解析】在题图③中，由折叠的性质可知∠A=45°，AD=DF，∴FC=2，∠AFC=45°，∴CG=2，∴FG=2，∴△GCF的周长为4+2.
13. 如图，在△ABC中，AC=BC=2，AB=1，将它沿AB翻折得到△ABD，则四边形ADBC的形状是　　　　形，点P，E，F分别为线段AB，AD，DB上的任意一点，则PE+PF的最小值是　　　　. 

【答案】菱　　【解析】∵AC=BC，∴△ABC是等腰三角形.将△ABC沿AB翻折得到△ABD，∴AC=BC=AD=BD，∴四边形ADBC是菱形.∵△ABC沿AB翻折得到△ABD，∴△ABC与△ABD关于AB成轴对称.如图所示，作点E关于AB的对称点E'，连接PE'，根据轴对称的性质知AB垂直平分EE'，∴PE=PE'，∴PE+PF=PE'+PF，当E'，P，F三点共线，且E'F⊥AC时，PE+PF有最小值，该最小值即为平行线AC与BD间的距离.作CM⊥AB于M，BG⊥AD于G，由题知AC=BC=2，AB=1，∠CAB=∠BAD，∴cos∠CAB=cos∠BAD，即=，∴AG=，在Rt△ABG中，BG===，由对称性可知BG长即为平行线AC，BD间的距离，∴PE+PF的最小值=.
三、解答题（本大题共2道小题）14. 如图，对折矩形纸片ABCD，使AB与DC重合，得到折痕MN，将纸片展平;再一次折叠，使点D落到MN上的点F处，折痕AP交MN于E;延长PF交AB于G.求证:(1)△AFG≌△AFP;(2)△APG为等边三角形.
【答案】证明:(1)∵对折矩形纸片ABCD，使AB与CD重合，得到折痕MN，∴MN∥AB，M，N分别为AD，BC中点，由平行线的性质可知PF=GF.由折叠的性质得∠PFA=∠GFA=90°，∴△AFG≌△AFP(SAS).(2)∵△AFG≌△AFP，∴AP=AG，∠2=∠3.又∵∠2=∠1，∴∠1=∠2=∠3.又∵∠1+∠2+∠3=90°，∴3∠2=90°，∴∠2=30°，∠PAG=2∠2=60°，∴△APG为等边三角形.
15. 如图①，等腰直角三角形OEF的直角顶点O为正方形ABCD的中心，点C，D分别在OE和OF上，现将△OEF绕点O逆时针旋转角α(0°<α<90°)，连接AF，DE(如图K32-②).(1)在图②中，∠AOF=　　　　;(用含α的式子表示) (2)在图②中，猜想AF与DE的数量关系，并证明你的结论.②      ②【答案】解:(1)90°-α　【解析】∵△OEF绕点O逆时针旋转角α，∴∠DOF=∠COE=α，∵四边形ABCD为正方形，∴∠AOD=90°，∴∠AOF=90°-α.故答案为90°-α.(2)AF=DE.证明:∵四边形ABCD为正方形，∴∠AOD=∠COD=90°，OA=OD，∵∠DOF=∠COE=α，∴∠AOF=∠DOE.∵△OEF为等腰直角三角形，∴OF=OE.在△AOF和△DOE中，∴△AOF≌△DOE(SAS)，∴AF=DE.