初中数学中考复习 专题7　实验操作型问题课件PPT

这是一份初中数学中考复习 专题7　实验操作型问题课件PPT，共31页。PPT课件主要包含了专题解读，精讲释疑等内容，欢迎下载使用。
实验操作问题主要包括剪纸、折叠、展开、拼图、作图(不包括统计图表的制作)、称重、测量、空间想象等．
解答操作型试题，关键是审清题意，学会运用图形的平移变换、翻折变换和旋转变换、位似变换，注意运用分类讨论、类比猜想、验证归纳等数学思想方法，在平时的学习中，要注重操作习题解题训练，提高思维的开放性，培养创新能力，要学会运用数学知识去观察、分析、抽象、概括所给的实际问题，揭示其数学本质，并转化为我们所熟悉的数学问题．
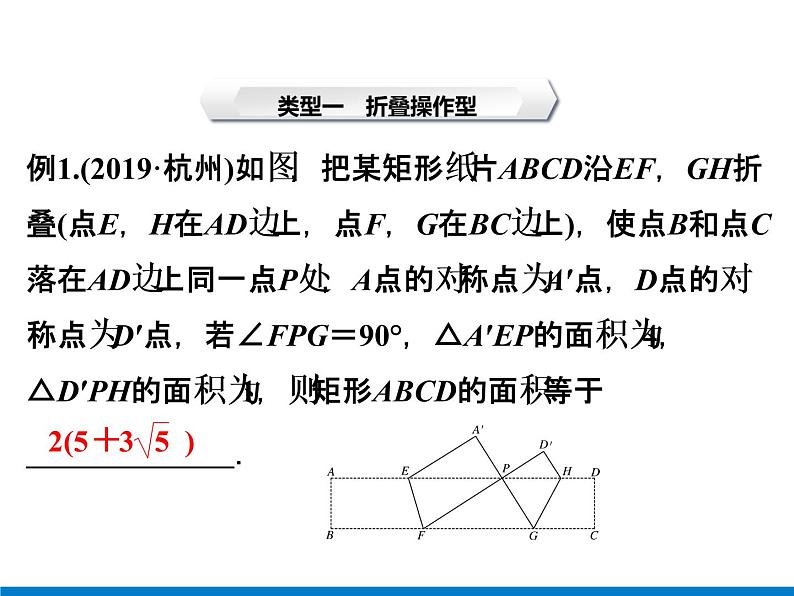
例1.(2019·杭州)如图，把某矩形纸片ABCD沿EF，GH折叠(点E，H在AD边上，点F，G在BC边上)，使点B和点C落在AD边上同一点P处，A点的对称点为A′点，D点的对称点为D′点，若∠FPG＝90°，△A′EP的面积为4，△D′PH的面积为1，则矩形ABCD的面积等于 ．
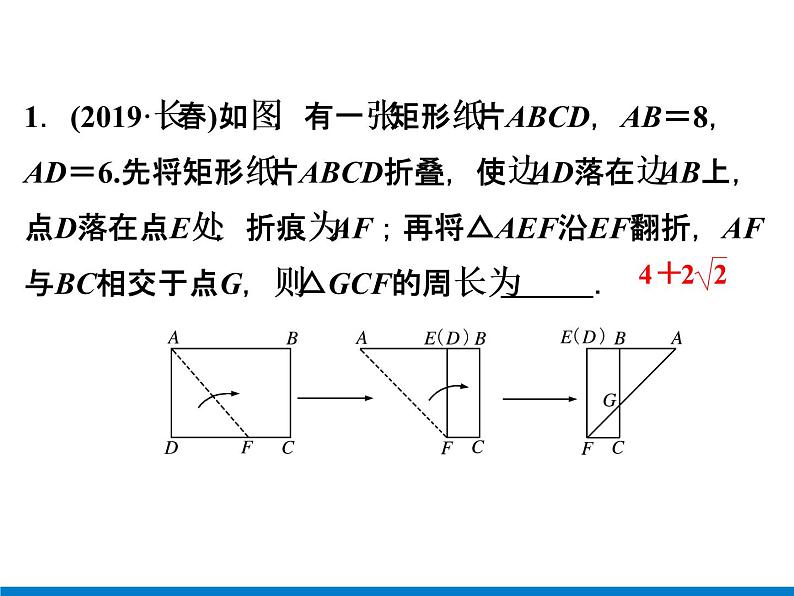
1．(2019·长春)如图，有一张矩形纸片ABCD，AB＝8，AD＝6.先将矩形纸片ABCD折叠，使边AD落在边AB上，点D落在点E处，折痕为AF；再将△AEF沿EF翻折，AF与BC相交于点G，则△GCF的周长为 ．
例2.(2019·聊城)如图，在等腰直角三角形ABC中，∠BAC＝90°，一个三角尺的直角顶点与BC边的中点O重合，且两条直角边分别经过点A和点B，将三角尺绕点O按顺时针方向旋转任意一个锐角，当三角尺的两直角边与AB，AC分别交于点E，F时，下列结论中错误的是( )
例3.(2019·绍兴)有一块形状如图的五边形余料ABCDE，AB＝AE＝6，BC＝5，∠A＝∠B＝90°，∠C＝135°，∠E＞90°，要在这块余料中截取一块矩形材料，其中一条边在AE上，并使所截矩形材料的面积尽可能大．(1)若所截矩形材料的一条边是BC或AE，求矩形材料的面积．
(2)能否截出比(1)中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由．
解：(1)①若所截矩形材料的一条边是BC，如图1所示：过点C作CF⊥AE于F，S1＝AB·BC＝6×5＝30；②若所截矩形材料的一条边是AE，如图2所示：过点E作EF∥AB交CD于F，FG⊥AB于G，过点C作CH⊥FG于H，则四边形AEFG为矩形，四边形BCHG为矩形，∵∠C＝135°，∴∠FCH＝45°，∴△CHF为等腰直角三角形，∴AE＝FG＝6，HG＝BC＝5，∴BG＝CH＝FH＝FG－HG＝6－5＝1，∴AG＝AB－BG＝6－1＝5，∴S2＝AE·AG＝6×5＝30；
(2)能；理由如下：在CD上取点F，过点F作FM⊥AB于M，FN⊥AE于N，过点C作CG⊥FM于G，则四边形ANFM为矩形，四边形BCGM为矩形，∵∠C＝135°，∴∠FCG＝45°，∴△CGF为等腰直角三角形，∴MG＝BC＝5，BM＝CG，FG＝CG，设AM＝x，则BM＝6－x，∴FM＝GM＋FG＝GM＋CG＝BC＋BM＝11－x，∴S＝AM×FM＝x(11－x)＝－x2＋11x＝－(x－5.5)2＋30.25，∴当x＝5.5时，S的最大值为30.25.
4．(2019·湖州)在数学拓展课上，小明发现：若一条直线经过平行四边形对角线的交点，则这条直线平分该平行四边形的面积．如图是由5个边长为1的小正方形拼成的图形，P是其中4个小正方形的公共顶点，小强在小明的启发下，将该图形沿着过点P的某条直线剪一刀，把它剪成了面积相等的两部分，则剪痕的长度是( )
5．(2019·绍兴)把边长为2的正方形纸片ABCD分割成如图的四块，其中点O为正方形的中心，点E，F分别为AB，AD的中点．用这四块纸片拼成与此正方形不全等的四边形MNPQ(要求这四块纸片不重叠无缝隙)，则四边形MNPQ的周长是 ．
例4.(2019·嘉兴)小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．(1)温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝6，AD＝4，求正方形PQMN的边长；
(2)操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P′，画正方形P′Q′M′N′，使Q′，M′在BC边上，N′在△ABC内，连结BN′并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN.小波把线段BN称为“波利亚线”；
(3)推理：证明图2中的四边形PQMN是正方形；(4)拓展：在(2)的条件下，在射线BN上截取NE＝NM，连结EQ，EM(如图3).当tan ∠NBM＝ 时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．
6．(2019·盐城)如图①是一张矩形纸片，按以下步骤进行操作：(Ⅰ)将矩形纸片沿DF折叠，使点A落在CD边上点E处，如图②；(Ⅱ)在第一次折叠的基础上，过点C再次折叠，使得点B落在边CD上点B′处，如图③，两次折痕交于点O；(Ⅲ)展开纸片，分别连接OB，OE，OC，FD，如图④.
【探究】(1)证明：△OBC≌△OED；(2)若AB＝8，设BC为x，OB2为y，求y关于x的关系式．