第九章 章末素养提升课件PPT

这是一份第九章 章末素养提升课件PPT，共38页。

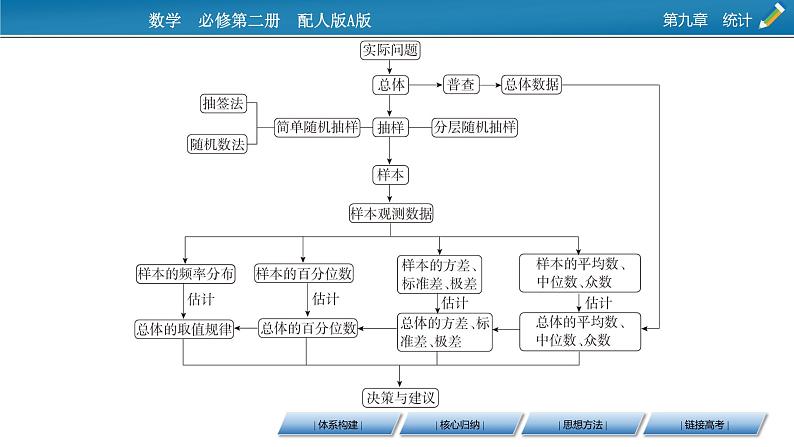
第九章　统计章末素养提升| 体系构建 || 核心归纳 |1．抽样方法(1)用随机数法抽样时，对个体所编号码位数要相同，当问题所给位数不同时，以位数较多的为准，在位数较少的数前面添“0”，凑齐位数．(2)分层抽样是按比例抽样，每一层入样的个体数为该层的个体数乘抽样比．(3)二种抽样方法的异同点2.用样本估计总体(1)用样本估计总体用样本频率分布估计总体频率分布时，通常要对给定的一组数据作频率分布表与频率分布直方图．(2)常见的统计图常见的统计图有条形统计图、折线统计图、扇形统计图等．(3)样本的数字特征样本的数字特征可分为两大类：一类是反映样本数据集中趋势的，包括众数、中位数和平均数；另一类是反映样本数据稳定程度或波动大小的，包括方差及标准差．| 思想方法 |(一)数形结合思想思想方法解读：涉及统计图，实质就是借助于数形结合思想来解决，利用直观图形所表现的或蕴含的数字特征来估计总体． 对某校高三年级学生参加社区服务的次数进行统计，随机抽取M名学生，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布表和频率分布直方图，如图所示：(1)求表中M，p及图中a的值；(2)若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数．利用数形结合思想求解与频率分布直方图有关问题的策略(1)已知频率分布直方图中的部分数据，求其他数据，可根据频率分布直方图中的数据求出样本与整体的关系，利用频率和等于1可求出其他数据．(2)已知频率分布直方图，求某种范围内的数据，可利用图形及某范围结合求解．1．如图所示是某学校某年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接．给出下列结论：①一班成绩始终高于年级平均水平，整体成绩比较好；②二班成绩不够稳定，波动程度较大；③三班成绩虽然多数时间低于年级平均水平，但在稳步提升．其中正确结论的个数为 (　　)A．0　　 B．1　　C．2　　 D．3【答案】D【解析】①由图可知一班每次考试的平均成绩都在年级平均成绩之上，故①正确．②由图可知二班平均成绩的图象高低变化明显，可知成绩不稳定，波动程度较大，故②正确．③由图可知三班平均成绩的图象呈上升趋势，并且图象的大部分都在年级平均成绩图象的下方，故③正确．故选D．(二)方程思想思想方法解读：在本章的抽样计算中，常常运用方程思想来解决样本数或总体数、中位数等． 一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量(单位：辆)如下表：按类用分层随机抽样的方法在这个月生产的轿车中抽取50辆，其中A类轿车有10辆．(1)求z的值；(2)用分层随机抽样的方法从C类轿车中抽取一个容量为5的样本，求舒适型、标准型的轿车应分别抽取多少辆？利用方程思想解决与分层随机抽样有关问题的策略(1)依据各层总数与样本数之比，确定抽样比．(2)求某一层的样本数或总体个数时，可先求出抽样比，再由某层总体个数(或样本数)确定该层的样本(或总体)数．(3)求各层的样本数，可先求出各层的抽样比，再求出各层样本数．(4)在频率分布直方图中，利用中位数两边图形面积相等，可列方程解决问题．2．(1)某学校高一、高二、高三三个年级共有430名学生，其中高一年级学生160名，高二年级学生180名，为了解学生身体状况，现采用分层随机抽样方法进行调查，在抽取的样本中高二学生有32人，则该样本中高三学生人数为________．(2)某单位有职工960人，其中青年职工420人，中年职工300人，老年职工240人，为了了解该单位职工的健康情况，用分层随机抽样的方法从中抽取样本，若样本中的青年职工为14人，则样本量为________．【答案】(1)16　(2)32| 链接高考 |随机抽样 (2017年江苏)某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200,400,300,100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取________件．【答案】18【点评】分层抽样在抽样时要保证样本的结构和总体的结构保持一致，按照一定的比例，即样本容量和总体容量的比值，在各层中进行抽取．统计图 (2018年新课标Ⅰ)某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下扇形图：则下面结论中不正确的是 (　　)A．新农村建设后，种植收入减少B．新农村建设后，其他收入增加了一倍以上C．新农村建设后，养殖收入增加了一倍D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A【解析】设建设前经济收入为a，则建设后经济收入为2a，由题图可知：根据上表可知B，C，D结论均正确，结论A不正确，故选A．【点评】准确理解题目所给的两个扇形统计图是解决本题的关键． (2017年新课标Ⅲ)某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量(单位：万人)的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是 (　　)A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7,8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳【答案】A【解析】观察2014年的折线图，发现从8月至9月，以及10月开始的三个月接待游客量都是减少的，故A选项是错误的．故选A．【点评】将各选项逐一与折线统计图比较即可容易得到正确答案．数据的数字特征 (2019年新课标Ⅱ)演讲比赛共有9位评委分别给出某选手的原始评分，评定该选手的成绩时，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分.7个有效评分与9个原始评分相比，不变的数字特征是 (　　)A．中位数　　 B．平均数　　C．方差　　 D．极差【答案】A【解析】根据题意，从9个原始评分中去掉1个最高分、1个最低分，得到7个有效评分，7个有效评分与9个原始评分相比，最中间的一个数不变，即中位数不变．故选A．【点评】本题考查数据的数字特征，关键是掌握数据的平均数、中位数、方差、极差的定义． (2019年江苏)已知一组数据6,7,8,8,9,10，则该组数据的方差是________． (2019年新课标Ⅱ)某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；【点评】本题考查样本数据的平均值和方差的求法，考查运算求解能力，难度较低．