2022-2023 数学北师大版新中考精讲精练 考点16全等三角形

这是一份2022-2023 数学北师大版新中考精讲精练 考点16全等三角形，文件包含2022-2023数学北师大版新中考精讲精练考点16全等三角形解析版docx、2022-2023数学北师大版新中考精讲精练考点16全等三角形原卷版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
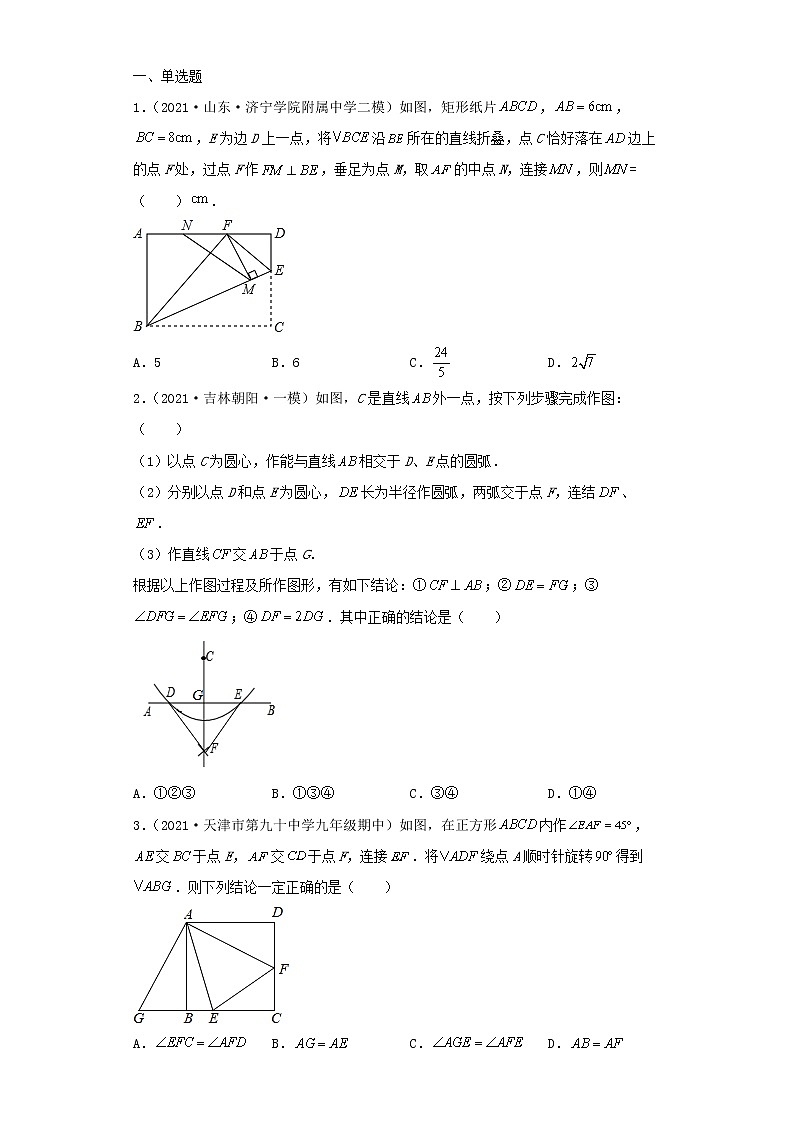
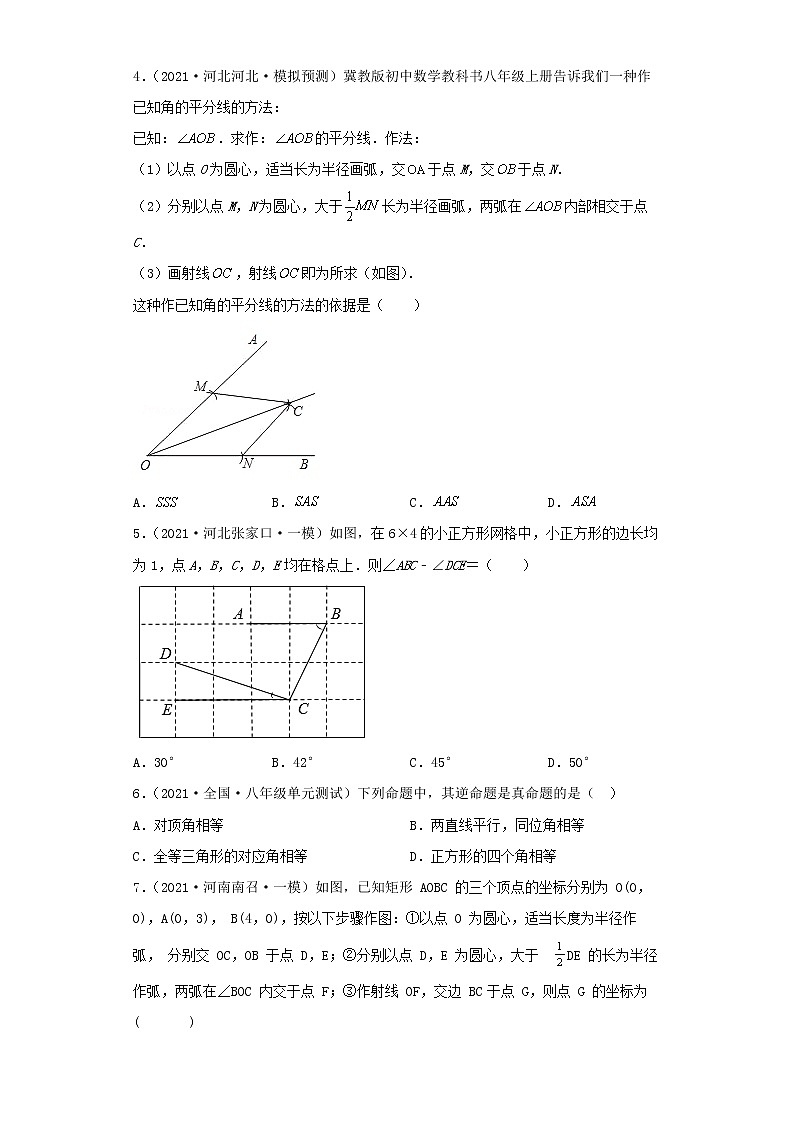
考点16全等三角形【考点总结】一、全等三角形的性质与判定1．概念：能够完全重合的两个三角形叫做全等三角形．2．性质：全等三角形的对应边、对应角分别相等．3．判定：(1)有三边对应相等的两个三角形全等，简记为(SSS)；(2)有两边和它们的夹角对应相等的两个三角形全等，简记为(SAS)；(3)有两角和它们的夹边对应相等的两个三角形全等，简记为(ASA)；(4)有两角和其中一角的对边对应相等的两个三角形全等，简记为(AAS)；(5)有斜边和一条直角边对应相等的两个直角三角形全等，简记为(HL)．【考点总结】二、定义、命题、定理、公理1．定义：对一个概念的特征、性质的描述叫做这个概念的定义．2．命题：判断一件事情的语句．(1)命题由题设和结论两部分组成．命题通常写成“如果…那么…”的形式，“如果”后面是题设，“那么”后面是结论．(2)命题的真假：正确的命题称为真命题；错误的命题称为假命题．(3)互逆命题：在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题称为互逆命题．每一个命题都有逆命题．3．定理：经过证明的真命题叫做定理．因为定理的逆命题不一定都是真命题．所以不是所有的定理都有逆定理．4．公理：有一类命题的正确性是人们在长期的实践中总结出来的，并把它们作为判断其他命题真伪的原始依据，这样的真命题叫公理．【考点总结】三、证明1．证明：从一个命题的条件出发，根据定义、公理及定理，经过逻辑推理，得出它的结论成立，从而判断该命题为真，这个过程叫做证明．2．证明的一般步骤：(1)审题，找出命题的题设和结论；(2)由题意画出图形，具有一般性；(3)用数学语言写出已知、求证；(4)分析证明的思路；(5)写出证明过程，每一步应有根据，要推理严密．3．反证法：先假设命题中结论的反面成立，推出与已知条件或是定义、定理等相矛盾，从而结论的反面不可能成立，借此证明原命题结论是成立的．这种证明的方法叫做反证法．真题演练 一、单选题1．（2021·山东·济宁学院附属中学二模）如图，矩形纸片，，，E为边D上一点，将沿所在的直线折叠，点C恰好落在边上的点F处，过点F作，垂足为点M，取的中点N，连接，则=（　　）．A．5 B．6 C． D．2．（2021·吉林朝阳·一模）如图，C是直线外一点，按下列步骤完成作图：（    ）（1）以点C为圆心，作能与直线相交于D、E点的圆弧．（2）分别以点D和点E为圆心，长为半径作圆弧，两弧交于点F，连结、．（3）作直线交于点G．根据以上作图过程及所作图形，有如下结论：①；②；③；④．其中正确的结论是（    ）A．①②③ B．①③④ C．③④ D．①④3．（2021·天津市第九十中学九年级期中）如图，在正方形内作，交于点E，交于点F，连接．将绕点A顺时针旋转得到．则下列结论一定正确的是（    ）A． B． C． D．4．（2021·河北河北·模拟预测）冀教版初中数学教科书八年级上册告诉我们一种作已知角的平分线的方法：已知：．求作：的平分线．作法：（1）以点O为圆心，适当长为半径画弧，交于点M，交于点N．（2）分别以点M，N为圆心，大于长为半径画弧，两弧在内部相交于点C．（3）画射线，射线即为所求（如图）．这种作已知角的平分线的方法的依据是（    ）A． B． C． D．5．（2021·河北张家口·一模）如图，在6×4的小正方形网格中，小正方形的边长均为1，点A，B，C，D，E均在格点上．则∠ABC﹣∠DCE＝（　　）A．30° B．42° C．45° D．50°6．（2021·全国·八年级单元测试）下列命题中，其逆命题是真命题的是（  ）A．对顶角相等 B．两直线平行，同位角相等C．全等三角形的对应角相等 D．正方形的四个角相等7．（2021·河南南召·一模）如图，已知矩形 AOBC 的三个顶点的坐标分别为 O(0，0)，A(0，3)， B(4，0)，按以下步骤作图：①以点 O 为圆心，适当长度为半径作弧， 分别交 OC，OB 于点 D，E；②分别以点 D，E 为圆心，大于  DE 的长为半径作弧，两弧在∠BOC 内交于点 F；③作射线 OF，交边 BC于点 G，则点 G 的坐标为(       )A．(4， ) B．(   ，4) C．( ，4) D．(4， )8．（2021·山东临淄·七年级期中）三个全等三角形按如图的形式摆放，则∠1+∠2+∠3的度数是（    ）A． B． C． D．9．（2021·江苏亭湖·一模）如图，已知△ABC中，AB=10 ，AC=8 ，BC = 6 ，DE是AC的垂直平分线，DE交AB于点D ，交AC于点E ，连接CD ，则CD的长度为（   ）A．3 B．4 C．4.8 D．510．（2021·青海·中考真题）如图，在四边形ABCD中，∠A=90°，AD=3，BC=5，对角线BD平分∠ABC，则△BCD的面积为（ ）A．7.5 B．8 C．15 D．无法确定 二、填空题11．（2021·青岛广雅中学（山东省青岛实验初级中学市北分校）九年级期中）如图，在正方形ABCD中，对角线AC与BD相交于点O，点E在AD的延长线上，连接CE，点F是CE的中点，连接OF交CD于点G．若DE=1，OF=1.5，则点C到DF的距离为______．12．（2021·广东白云·二模）将5个边长都为2的正方形按如图所示摆放，点，，……，分别是正方形的中心，则这5个正方形两两重叠（阴影）部分的面积之和是______；若按此规律摆放个这样的正方形，则这个正方形两两重叠（阴影）部分的面积之和是______．
 13．（2021·全国·八年级专题练习）如图，直线l为线段的垂直平分线，垂足为C，直线l上的两点E，F位于异侧（E，F两点不与点C重合）．只需添加一个条件即可证明，这个条件可以是____．14．（2021·浙江南浔·一模）我国古代数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的三角形，如图所示，已知，则的长度是_________．三、解答题15．（2021·山东青岛·中考真题）已知：及其一边上的两点，．求作：，使，且点在内部，．16．（2021·山东青岛·中考真题）如图，在中，为边的中点，连接并延长，交的延长线于点，延长至点，使，分别连接，，．（1）求证：；（2）当平分时，四边形是什么特殊四边形？请说明理由．17．（2021·江西·新余市第一中学模拟预测）如图，在正方形中，点、分别在边和上，且，连接、，其相交于点，将沿翻折得到，延长交延长线于点．（1）求证：；（2）若，，求的长．