2022-2023 数学北师大版新中考精讲精练 考点17多边形与平行四边形

这是一份2022-2023 数学北师大版新中考精讲精练 考点17多边形与平行四边形，文件包含2022-2023数学北师大版新中考精讲精练考点17多边形与平行四边形解析版docx、2022-2023数学北师大版新中考精讲精练考点17多边形与平行四边形原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
考点17多边形与平行四边形【考点总结】一、多边形的有关概念及性质1．多边形的概念定义：在平面内，由一些不在同一直线上的线段首尾顺次相接组成的图形叫做多边形．对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．正多边形：各个角都相等，各条边都相等的多边形叫做正多边形．2．性质：n边形的内角和为(n－2)·180°，外角和为360°.【考点总结】二、平面图形的密铺(镶嵌)1．密铺的定义：用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的密铺，又称作平面图形的镶嵌．2．平面图形的密铺：正三角形、正方形、正六边形都可以单独使用密铺平面，部分正多边形的组合也可以密铺．【考点总结】三、平行四边形的定义和性质1．定义：两组对边分别平行的四边形叫做平行四边形．2．性质：(1)平行四边形的对边相等且平行．(2)平行四边形的对角相等．(3)平行四边形的对角线互相平分．(4)平行四边形是中心对称图形．【考点总结】四、平行四边形的判定1．两组对边分别相等的四边形是平行四边形．2．两组对边分别平行的四边形是平行四边形．3．一组对边平行且相等的四边形是平行四边形．4．对角线相互平分的四边形是平行四边形．5．两组对角分别相等的四边形是平行四边形．真题演练 一、单选题1．（2021·内蒙古呼和浩特·中考真题）如图，正方形的边长为4，剪去四个角后成为一个正八边形，则可求出此正八边形的外接圆直径d，根据我国魏晋时期数学家刘的“割圆术”思想，如果用此正八边形的周长近似代替其外接圆周长，便可估计的值，下面d及的值都正确的是（   ）A．， B．，C．， D．，【答案】C【分析】根据勾股定理求出多边形的边长，利用多边形内角和求解内角度数，再根据锐角三角函数求值即可．【详解】解： 设剪去△ABC边长AC=BC=x，可得：，解得x=，则BD=，∵正方形剪去四个角后成为一个正八边形，根据正八边形每个内角为135度，，则∠BFD=22.5°，∴外接圆直径d=BF=，根据题意知周长÷d==，故选：C．2．（2021·贵州铜仁·中考真题）用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌．工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌（      ）A．等边三角形 B．正方形 C．正五边形 D．正六边形【答案】C【分析】进行平面镶嵌就是在同一顶点处的几个多边形的内角和应是，因此我们只需要验证是不是上面所给的几个正多边形的一个内角度数的整数倍即可．【详解】解：A、等边三角形每个内角的度数为，，故该项不符合题意；B、正方形的每个内角的度数为，，故该项不符合题意； C、正五边形的每个内角的度数为，，故该项符合题意；D、正六边形的每个内角的度数为，，故该项不符合题意；故选：C．3．（2021·湖南·长沙市长郡双语实验中学一模）一个正多边形，它的每一个外角都等于40°，则该正多边形是（    ）A．正六边形 B．正七边形 C．正八边形 D．正九边形【答案】D【分析】根据多边形的外角和是360°， 正多边形的每一个外角都等于40°，直接用360÷40即得.【详解】解：360÷40=9.故答案为D.4．（2021·山东临沂·一模）如图，在正五边形ABCDE中，连接BE，则∠ABE的度数为(      )A．30° B．36° C．54° D．72°【答案】B【分析】在等腰三角形△ABE中，求出∠A的度数即可解决问题．【详解】解：在正五边形ABCDE中，∠A=×（5-2）×180=108°
 又知△ABE是等腰三角形，
∴AB=AE，
∴∠ABE=（180°-108°）=36°．
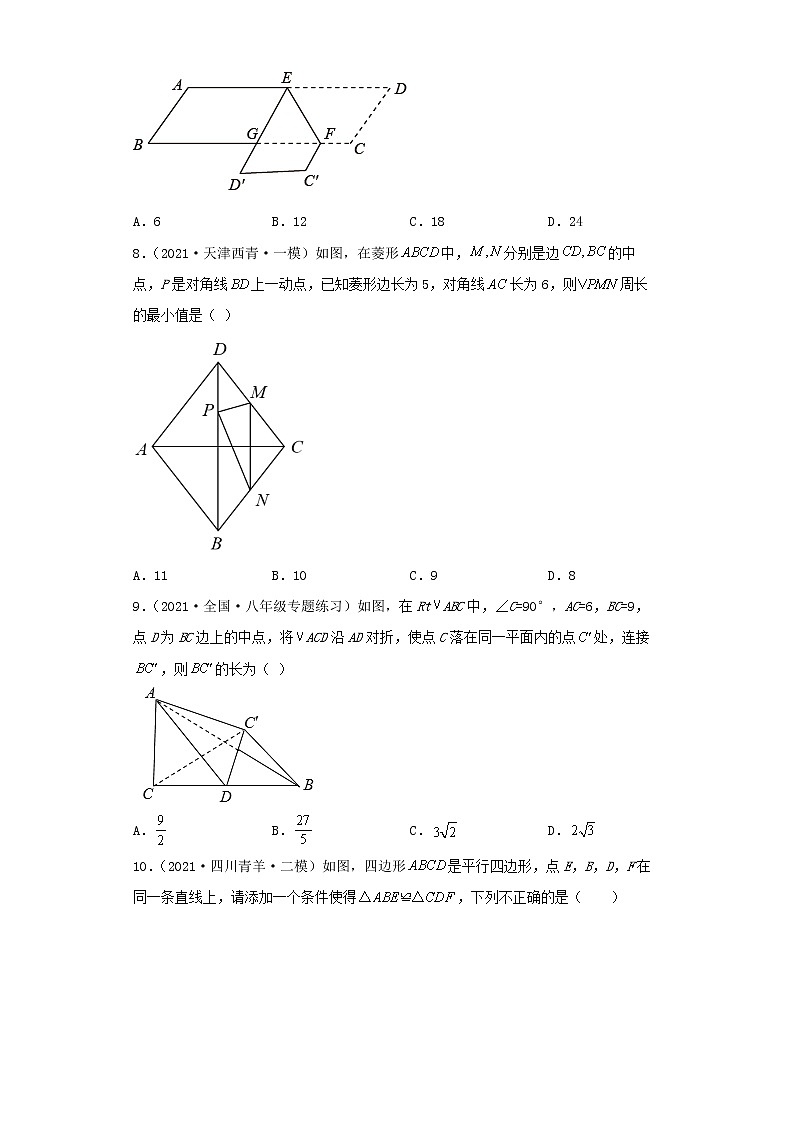
故选B．5．（2021·全国·九年级单元测试）下列说法中，正确的是（　　）A．“任意画一个多边形，其内角和是360°”是必然事件B．“如果a2＝b2，那么a＝b”是必然事件C．可能性是50%的事件，是指在两次试验中一定有一次会发生D．“从一副扑克牌（含大小王）中抽一张，恰好是红桃”是随机事件【答案】D【分析】根据题意逐项分析，即可求解．【详解】解：A. “任意画一个多边形，其内角和是360°”是必然事件，只有四边形的内角和是360°，所以是随机事件，判断错误；B. “如果a2＝b2，那么a＝b”是必然事件，a与b也有可能互为相反数，所以是随机事件，判断错误；C. 可能性是50%的事件，是指在两次试验中一定有一次会发生，可能性是50%的事件，只表明一种可能性，并不表示两次试验中一定有一次会发生，所以判断错误；D. “从一副扑克牌（含大小王）中抽一张，恰好是红桃”是随机事件，判断正确，符合题意．故选：D6．（2021·福建·模拟预测）将△ABC平移得到△，若，则的度数是（    ）A．10° B．80° C．100° D．160°【答案】B【分析】利用平移的性质证明四边形为平行四边形，根据对角相等即可解答．【详解】解：由题意作下图：由平移的性质知，，四边形为平行四边形，，，，故选：B．7．（2021·全国·八年级专题练习）如图，，分别是的边，上的点，，．将四边形沿翻折，得到，交于点．则的周长为（    ）A．6 B．12 C．18 D．24【答案】C【分析】由折叠得：∠DEF＝∠D′EF＝60°，再由平行四边形的对边平行，得出内错角相等，得出△GEF是等边三角形，已知边长求出周长即可．【详解】解：由折叠得：∠DEF＝∠D′EF＝60°，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DEF＝∠EFG＝60°，∴△GEF是等边三角形，∴EF＝FG＝GE＝6，∴△GEF的周长为6×3＝18，故选：C．8．（2021·天津西青·一模）如图，在菱形中，分别是边的中点，P是对角线上一动点，已知菱形边长为5，对角线长为6，则周长的最小值是（ ）A．11 B．10 C．9 D．8【答案】C【分析】作点M关于BD的对称点，连接交BD于点．根据轴对称、菱形的性质可知点为AD的中点．再根据题意即可证明经过点O，即点O与点重合．即当点为P点时，最小为长，即此时的周长最小．根据勾股定理可求出，再利用中位线的性质即可求出长，最后由，求出即为的周长最小值．【详解】如图，作点M关于BD的对称点，连接交BD于点．根据对称的性质和菱形的性质可知点为AD的中点．又∵点N为BC中点，∴经过点O，即点O与点重合．∵，∴根据两点直线线段最短可知，当点为P点时，最小为长，即此时的周长最小．∵AC=6，∴ ．在中，，∴．∵点M，N分别为DC，BC的中点，∴．∵点，N分别为AD，BC的中点，∴，又∵，∴四边形为平行四边形．∴，∴，即的周长最小值为9．故选：C．9．（2021·全国·八年级专题练习）如图，在RtABC中，∠C=90°，AC=6，BC=9，点D为BC边上的中点，将ACD沿AD对折，使点C落在同一平面内的点处，连接，则的长为（ ）A． B． C． D．【答案】B【分析】由折叠的性质可得AD⊥CC'，CN=C'N，由勾股定理可求AD，DN的长，即可求BC'的长．【详解】解：如图，连接CC'，
∵将△ACD沿AD对折，使点C落在同一平面内的点C'处，
∴AD⊥CC'，CN=C'N，
∵点D为BC边上的中点，∴CD=BC=AD=∵S△ACD=×AC×CD=×AD×CN∴CN= ∴DN=，∵CN=C'N，CD=DB，∴C'B=2DN=，故选：B．10．（2021·四川青羊·二模）如图，四边形是平行四边形，点E，B，D，F在同一条直线上，请添加一个条件使得，下列不正确的是（    ）A． B． C． D．【答案】A【分析】根据平行四边形的性质结合全等三角形的判定，逐项进行判断即可.【详解】解：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠ABD=∠BDC，∵∠ABE+∠ABD=∠BDC+∠CDF，∴∠ABE=∠CDF，A.若添加，则无法证明，故A错误；B.若添加，运用AAS可以证明，故选项B正确；C.若添加，运用ASA可以证明，故选项C正确；D.若添加，运用SAS可以证明，故选项D正确．故选：A． 二、填空题11．（2021·陕西·紫阳县师训教研中心八年级期末）如图，正方形和正方形的边长分别为和3cm，点、分别为、边上的点，为的中点，连接，则的长为_______．【答案】【分析】作辅助线构造直角三角形HMG，先根据三角形的中位线定理得到MN的长等于1，即可得到HM的长，再根据矩形的判定和性质得到GM=NP=1，最后由勾股定理即可得到HG的长．【详解】解：延长GF交AB于P，过H作HN⊥CD于M，交BC于N，∵四边形ABCD是正方形，∴AD//BC，AD⊥CD，∴MN⊥BC，∵四边形AEFG是正方形，∴FG⊥AD，∴FG//HM//CD，∵H是CF的中点，∴PN=CN=DM=GM==1，∴HN是△CFP的中位线，∴，∴，∴在Rt△GHM中，由勾股定理得：故答案为：．12．（2021·辽宁本溪·二模）如图，将边长为4的等边沿射线平移得到，点，分别为，的中点，点是线段的中点，连接，．当为直角三角形时，_____．【答案】4或8【分析】分∠APC=90°和∠ACP=90°两种情形求解即可．【详解】如图1，当∠APC=90°时，∵AM=MC，AC=4，∴PM是△APC斜边上的中线，∴AM=CM=PM=2，∴PN=2，∴MN=4，故将△ABC向右平移4个单位即可，∴BE=4；如图2，当∠ACP=90°时，∵△ABC是等边三角形，AM=MC，∴∠BMC=90°，∴∠BMC=∠ACP，∴BM∥CP，∵△ABC是等边三角形，△DEF是等边三角形，M，N分别是AC，DF的中点，∴∠ACB=∠DFE= 60°，CM=NF，∴MC∥NF，∴四边形MCFN是平行四边形，∴MP∥BC，∴四边形BCPM是平行四边形，∴PM=4，∴PN=4，∴MN=8，故将△ABC向右平移8个单位即可，∴BE=8；故答案为：4或8．13．（2021·浙江浙江·八年级期中）平行四边形ABCD的面积为36，AB＝5，BC＝9，则AC的长为_____．【答案】或．【分析】分两种情况：过点A作AE⊥BC于点E，根据面积求出AE=4，运用勾股定理求出BE=3，①.当AE在平行四边形内部时，求得CE=6，运用勾股定理楞求出AC的长；②当AE在平行四边形外部时，求得CE=12，运用勾股定理可求出AC的长．【详解】解：过点A作AE⊥BC于点E，如图①∵平行四边形ABCD的面积为36，BC＝9，∴ ∴AE=4在Rt△ABE中，AB=5，AE=4∴ ∴CE=BC-BE=9-3=6在Rt△AEC中，AE=4，EC=6∴ 如图②，同理可得AE=4，∴CE=BE+BC=3+9=12∴在Rt△AEC中，AE=4，EC=12∴ 所以，AC的长为或．故答案为：或．14．（2021·福建·漳州市普通教育教学研究室七年级期末）一个n边形的各内角都等于，则边数n是_______．【答案】6【分析】首先求出外角度数，再用360°除以外角度数可得答案．【详解】解：∵n边形的各内角都等于120°，∴每一个外角都等于180°-120°=60°，∴边数n=360°÷60°=6．故答案为：6．15．（2021·江苏秦淮·九年级期中）如图，五边形是正五边形，过点B作的垂线交于点F，则________．【答案】54゜【分析】利用多边形的内角和定理可得∠A=∠ABC=∠C=∠D=∠E==108°，由BF⊥AB，可得∠CBF的度数，利用三角形的内角和定理可得∠1，易得结果．【详解】解：∵五边形ABCDE是正五边形，∴∠A=∠ABC=∠C=∠D=∠E==108°，∵BF⊥AB，∴∠ABF=90°，∴∠CBF=∠ABC-∠ABF=108°-90°=18°，∴∠1=180°-∠C-∠CBF=180°-108°-18°=54°，∴∠C-∠1=108°-54°=54°，故答案为：54゜． 三、解答题16．（2021·黑龙江·哈尔滨市虹桥初级中学校二模）在△ABC中，∠CAB＝90°，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：四边形ADCF是菱形．（2）连接CE，若CE＝EF，直接写出长度等于的线段．【答案】（1）见解析；（2）BD，AD，CD，CF，FA．【分析】（1）先证明△AEF≌△DEB，通过对边平行且相等证明四边形ADCF为平行四边形，再由直角三角形斜边中线长等于斜边长的一半得四边形邻边相等，从而得出结论．（2）CE＝EF＝EB，点E在BC垂直平分线上，从而得出△ABC为等腰直角三角形，进而求解．【详解】证明：（1）∵AF//BC，∴∠FAE＝∠BDE，∵E为AD中点，∴AE＝DE，在△AEF和△DEB中，，∴△AEF≌△DEB（ASA），∴AF＝BD，∵AD为Rt△ABC的斜边中线，∴AD＝BD＝CD，∴AF＝AD＝CD，又∵AF//CD，∴四边形ADCF是菱形．（2）由（1）得E为BF中点，∵CE＝EF，∴CE＝BE，∴AD垂直平分BC，∴△ABC为等腰直角三角形，四边形CFAD为正方形，∴BD＝AD＝CD＝CF＝FA＝AB．故答案为：BD，AD，CD，CF，FA．17．（2021·江苏玄武·二模）如图，在中，，分别是，边上的点，，连接．，的平分线分别交，边于点，，连接，．（1）求证：四边形是平行四边形；（2）小明在完成（1）的证明后继续探索，他猜想：当为的中点时，四边形是矩形，请在下列框图中补全他的证明思路．小明的证明思路连接．由（1）知四边形是平行四边形．要证是矩形，只要证．故只要证．由已知条件______，故只要证，即证四边形为平行四边形．易证______故只要证，易证，故只要证______， 易证，即可得证．【答案】（1）证明见解析；（2）平分，，【分析】（1）结合题意，根据平行四边形性质，得；根据角平分线性质，得，，从而得；通过证明，得，即可完成证明；（2）根据角平分线、平行线性质，得，再根据全等三角形、矩形性质分析，即可得到答案．【详解】（1）∵四边形是平行四边形∴，∴∵，分别平分，∴，∴，∴在和中∴∴∴四边形是平行四边形（2）连接．由（1）知四边形是平行四边形．要证是矩形，只要证．故只要证．由已知条件平分，故只要证，即证四边形为平行四边形．易证故只要证，易证，故只要证， 易证，即可得证．故答案为：平分，，．