



2022-2023 数学京改版中考精讲精练 考点01实数的有关概念和计算
展开考点01实数的有关概念和计算
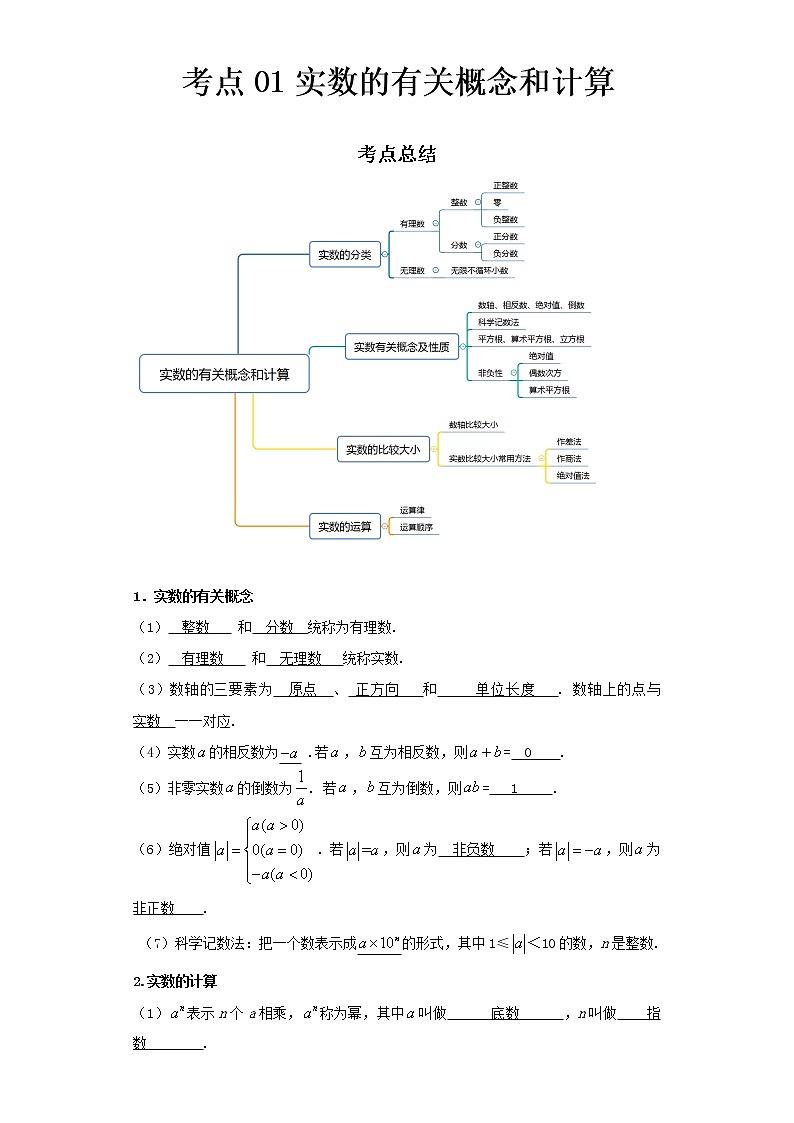
考点总结
1.实数的有关概念
(1) 整数 和 分数 统称为有理数.
(2) 有理数 和 无理数 统称实数.
(3)数轴的三要素为 原点 、 正方向 和 单位长度 . 数轴上的点与 实数 一一对应.
(4)实数的相反数为 .若,互为相反数,则= 0 .
(5)非零实数的倒数为. 若,互为倒数,则= 1 .
(6)绝对值.若,则为 非负数 ;若,则为 非正数 .
(7)科学记数法:把一个数表示成的形式,其中1≤<10的数,n是整数.
2.实数的计算
(1)表示n个a相乘,称为幂,其中叫做 底数 ,n叫做 指数 .
1 (其中 ≠ 0);0的任何非零次幂都等于0;
(其中 ≠ 0,p为整数)
(2)平方根:如果一个数x的平方等于a,即,那么这个数x叫做a的平方根或二次方根,记为.
一个正数有 两个 平方根,它们互为 相反数 ;负数没有平方根;0的平方根是 0 .
(3)算术平方根:如果一个正数x的平方等于a,则这个正数x为a的算术平方根,记为.
一个正数有 一个 算术平方根,0的算术平方根是 0 .
(4)立方根:一个数x的立方等于a,那么这个数x叫做a的立方根或三次方根,记为.
一个正数有一个正的立方根;一个负数有一个 负 的立方根;0的立方根是 0 .
3. 实数运算顺序及运算律
(1)先算 乘方 ,再算 乘除 ,最后算 加减 ;如果有括号,先算 括号 里面的,同一级运算按照从 左 到 右 的顺序依次进行.
(2)运算律:交换律、结合律、乘法分配律.
4. 实数大小的比较
(1) 数轴上两个点表示的数, 右边 的点表示的数总比 左边 的点表示的数大.
(2)正数 大于 0,负数 小于 0,正数 大于 负数;两个负数比较大小,绝对值大的
小于 绝对值小的.
真题演练
一、单选题
1.已知.若为整数且,则的值为( )
A.43 B.44 C.45 D.46
2.实数在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A. B. C. D.
3.下列各数中,小于的正整数是( )
A.-1 B.0 C.1 D.2
4.A,B是数轴上位于原点O异侧的两点(点A在点B的左侧),若点A,B分别对应的实数为a,b,且,则中最大的数是( )
A. B. C. D.
5.若实数p,q,m,n在数轴上的对应点的位置如图所示,且满足,则绝对值最小的数是( )
A.p B.q C.m D.n
6.比大,比小的整数是( )
A.1 B.2 C.3 D.4
7.若实数a,b在数轴上的对应点的位置如图所示,则以下结论正确的是( )
A. B. C. D.
8.将边长分别为2和4的长方形如图剪开,拼成一个正方形,则该正方形的边长最接近整数( )
A.1 B.2 C.3 D.4
9.已知实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A.a>b B.-a>b C.ab>0 D.|a|<|b|
10.数轴上A,B,C,D四点中,有可能在以原点为圆心,以为半径的圆上的点是( )
A.点A B.点B C.点C D.点D
二、填空题
11.请写出一个大于2而小于3的无理数___.
12.如图所示的网格是正方形网格,A,B,C,D 是网格线交点,则△ABC与△DBC面积的大小关系为:S△ABC ______ S△DBC(填“>”,“=”或“<”).
13.已知,则________.
14.若的值为有理数,请你写出一个符合条件的实数a的值_________.
15.比大的整数中,最小的是_______.
三、解答题
16.先化简再求值:,其中.
17.在平面直角坐标系中,任意两点,,定义线段的“直角长度”为.
(1)已知点.
① ________;
② 已知点,若,求m的值;
(2)在三角形中,若存在两条边“直角长度”之和等于第三条边的“直角长度”,则称该三角形为“和距三角形”.已知点.
① 点.如果为“和距三角形”,求d的取值范围;
② 在平面直角坐标系中,点C为直线上一点,点K是坐标系中的一点,且满足,当点C在直线上运动时,点K均满足使为“和距三角形”,请你直接写出点C的横坐标的取值范围.
18.计算:.
2022-2023 数学浙教版新中考精讲精练 考点01实数的有关概念和计算: 这是一份2022-2023 数学浙教版新中考精讲精练 考点01实数的有关概念和计算,文件包含2022-2023数学浙教版新中考精讲精练考点01实数的有关概念和计算解析版docx、2022-2023数学浙教版新中考精讲精练考点01实数的有关概念和计算原卷版docx等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
2022-2023 数学鲁教版新中考精讲精练 考点01 实数: 这是一份2022-2023 数学鲁教版新中考精讲精练 考点01 实数,文件包含2022-2023数学鲁教版新中考精讲精练考点01实数解析版docx、2022-2023数学鲁教版新中考精讲精练考点01实数原卷版docx等2份试卷配套教学资源,其中试卷共11页, 欢迎下载使用。
2022-2023 数学京改版新中考精讲精练 考点30概率及有关计算: 这是一份2022-2023 数学京改版新中考精讲精练 考点30概率及有关计算,文件包含2022-2023数学京改版新中考精讲精练考点30概率及有关计算解析版docx、2022-2023数学京改版新中考精讲精练考点30概率及有关计算原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












