




2022-2023 数学京改版新中考精讲精练 中考模拟卷(三)
展开中考模拟卷(三)
一、单选题
1.如图,在菱形中,,,点P为对角线上的一个动点,过P作交于点E,交于点F,将沿折叠,点A的对应点恰好落在对角线上的点G处,若是等腰三角形时,则的长为( )
A.或 B.或2 C.或4 D.或
【答案】B
【分析】
分CG=CB和GC=GB两种情形,分别求解即可.
【详解】
解:连接DB,交AC于点O,则DB⊥AC.
∵EF ⊥AC,
∴EF//DB
∵,
∴∠CAB= ∠CAD= ∠BCA=30°,
∵
∴AD=AB=BC=DB=,DO=BO=
∵DB⊥AC
∴AO= ,即AC=6
当GC=CB=,AP=(AC-CG)=(6-)=3-;
当GB=GC时,过点G做GH⊥BC,则CH=BC=
∵∠BCA=30°
∴
∴GC= 2,
∴AP=(AC-CG)=(6-2)=2;
综上,AP的长为3-或2.
故选B.
2.如图,已知在平面直角坐标系中,反比例函数在第一象限经过的顶点A,且点B在轴上,过点B作轴的垂线交反比例函数图像于点C,连结OC交AB于点D,已知,,则的值为( )
A.6 B.8 C. D.
【答案】C
【分析】
过A向OB作垂线,垂足为F,交OC于E,根据AF∥BC,得出,设,则AF=tBC,得,又,可推导出,求出t的值,得出AF=2BC,OB=2OF进一步导出OA=3OF,在Rt△AOF中,AF=,,在Rt△OBC中,即可求出OF的长,求出k的值.
【详解】
解:如图,过A作AF垂直OB于F点,交OC于E点,
∴AF∥BC,
∴△AED∽△BCD,
∴,
∴,
设,则AF=tBC,
∴
又OF×AF=OB×BC,
∴,
又EF∥BC,
∴△OEF∽△OCB
∴,
∴,
解得t=2,
∴AF=2BC,OB=2OF
又∵,
∴,
∴OA=3OF,
在Rt△AOF中,勾股定理可得AF=,
∴,
在Rt△OBC中,,
∴,
解得OF= 或﹣(舍去)
∴AF==4,
∴k=OF×AF=,
故选:C.
3.如图,在矩形ABCD中,,,点E为AB上一点,连接DE,将沿DE折叠,点A落在处,连接,若F,G分别为,BC的中点,则FG的最小值为( )
A.2 B. C. D.1
【答案】D
【分析】
分别连接BD、;根据矩形和勾股定理的性质,得;根据轴对称性质,得;当点不在BD上时,根据三角形边角关系的性质,得,当点在BD上时,得,即可得到最小值,再结合三角形中位线的性质计算,即可得到答案.
【详解】
如图,分别连接BD、
∵矩形ABCD中,,
∴
∴
∵将沿DE折叠,点A落在处,
∴
当点不在BD上时,
∴
当点在BD上时,
∴最小值为2
∵F,G分别为,BC的中点
∴为的中位线
∴
∴FG的最小值为1
故选:D.
4.如图,在△ABC中,AC=BC=4,∠C=90°,D是BC边上一点,且CD=3BD,连接AD,把△ACD沿AD翻折,得到△ADC',DC′与AB交于点E,连接BC′,则△BDC'的面积为( )
A. B. C. D.
【答案】B
【分析】
先求出BD,CD,进而求出AD,再构造直角三角形,判断出△BDE∽△ADC,求出DE=,BE=,进而求出S△BDE=,AE=,再判断出△AHE∽△ADC,求出AH=7,HE=,再判断出△BFH∽△ACD,求出BF=,最后用三角形的面积的差,即可得出结论.
【详解】
解:∵CD=3BD,BC=4,
∴BD=1,CD=3,
∴S△ACD=AC•CD=6,
在Rt△ACD中,根据勾股定理得,AD==5,
过点B作BE⊥AD交AD的延长线于E,
∴∠BED=90°=∠C,
∵∠BDE=∠ADC,
∴△BDE∽△ADC,
∴,
∴,
∴DE=,BE=,
∴S△BDE=DE•BE=,AE=AD+DE=,
延长EB交AC的延长线于H,
由折叠知,S△AC'D=S△ACD=6,AC'=AC=4,∠C'AD=∠CAD,
∵∠C=∠AEH=90°,
∴△AHE∽△ADC,
∴,
∴,
∴AH=7,HE=,
∴C'H=AH﹣AC'=3,BH=HE﹣BE=,S△AHE=AE•HE=,
过点B作BF⊥C'H于F,
∴∠BFH=90°=∠C,
∴∠H+∠FBH=90°,
∵∠C'AD+∠H=90°,
∴∠FBH=∠C'AD=∠CAD,
∴△BFH∽△ACD,
∴,
∴,
∴BF=,
∴S△BC'H=C'H•BF=,
∴S△BC'D=S△AEH﹣S△BDE﹣S△BC'H﹣S△AC'D=﹣﹣﹣6=,
故选:B.
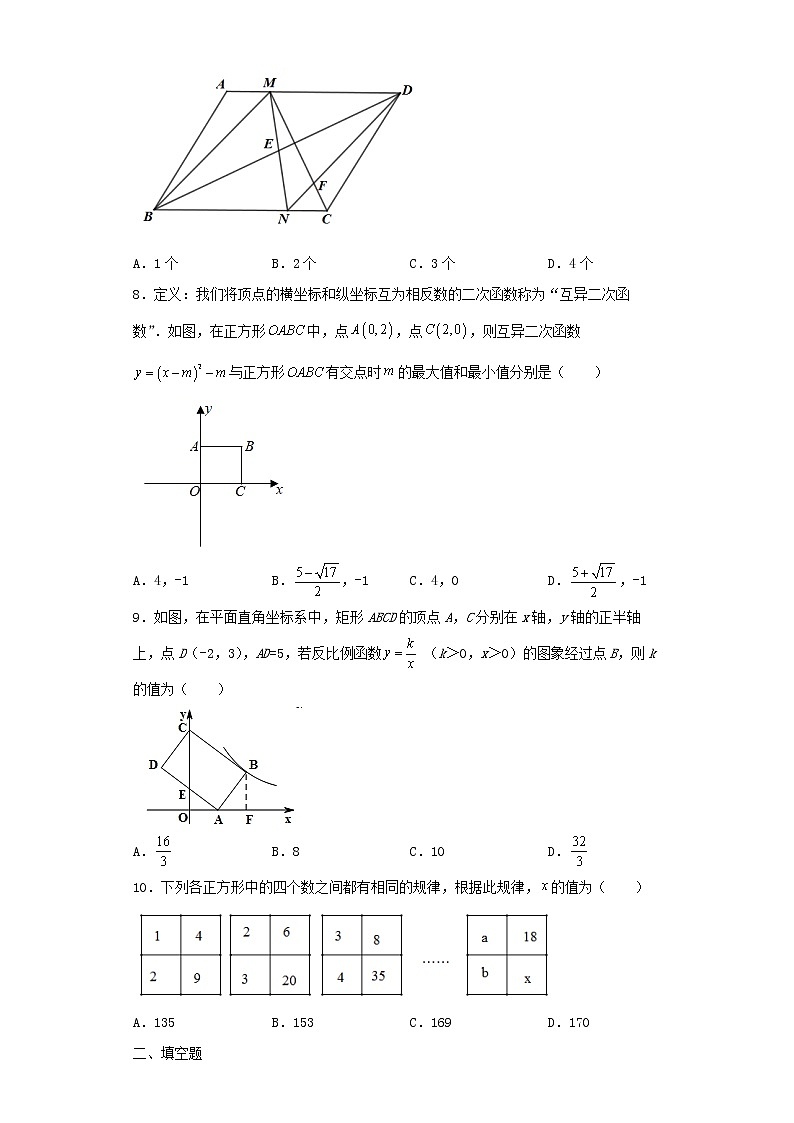
5.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:①∠BAE=∠EAF;②射线FE是∠AFC的角平分线;③CF=CD;④AF=AB+CF.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】
①设正方形的边长为2,然后求出AE、FC、EF,然后比较正切函数值即可;
②由已知条件,可得∠AEB和∠CFE的正切值,从而可以得到射线FE是否为∠AFC的角平分线;
④结合②③的结论,确定CF和CD的关系,从而可以判断CF=CD是否成立;
④由已知条件和全等三角形的判定与性质以及线段的和差即可判定AF=AB+CF是否成立.
【详解】
解:设正方形的边长为2
∵在正方形ABCD中, E是BC的中点
∴AB=BC=2,BE=EC=AB=1,∠C=∠B=90°,
∴AE=,tan∠BAE=
∵∠BAE+∠AEB=90°,∠AEB+∠BAE =90°,
∴∠BAE=∠BAE
∴tan∠FEC=,CE=1
∴CF=
∴EF=
∴tan∠EAF =
∴∠BAE=∠EAF,故①正确;
∴tan∠CFE=,tan∠AFE=,
∴∠AFE=∠CFE,即射线FE是∠AFC的角平分线,故②正确;
∵BC=CD,BC=2CE=4CF,
∴CF=CD,故③正确;
作EG⊥AF于点G,
∵FE平分∠AFC,∠C=90°,
∴EG=EC,
∴EG=EB,
∵∠B=∠AGE=90°,
在Rt△ABE和Rt△AGE中
AE=AE,EB=EG
∴Rt△ABE≌Rt△AGE(HL)
∴AB=AG,
又∵CF=GF,AF=AG+GF,
∴AF=AB+CF,故④正确;
综上共有4个正确结论.
故答案为D.
6.如图,正方形中,,点是对角线上一点,连接,过点作,交于点,连接,交于点,将沿翻折,得到,连接,交于点,若点是的中点,则的周长是( )
A. B.
C. D.
【答案】C
【分析】
如图:过E作PQ⊥DC,交DC于P,交AB于Q,连接BE.先通过等腰三角形和全等三角形的判定和性质得到FQ=BQ=PE=1;再说明△DEF是等腰直角三角形,然后再利用勾股定理计算得到DE=EF=;如图2,由DC//AB可得△DGC∽△FGA,列比例式可求FG和CG的长,从而得EG的长;然后再根据AGHF是等腰直角三角形,求得GH和FH的长;利用DE∥GM证明△DEN∽△MNH,则可得EN=,然后计算出△EMN各边的长,最后求周长即可.
【详解】
解:如图1:过E作PQ⊥DC,交DC于P,交AB于Q,连接BE.
∵DC∥AB
∴PQ⊥AB,
∴四边形ABCD是正方形
∴∠ACD=450
∴△PEC是等腰直角三角形
∴PE=PC.
设PC=x,则PE=x,PD=4-x,EQ=4-x.
∴PD=EQ,
∴∠DPE=∠EQF=90°,∠PED=∠EFQ.
∴△DPE≌△EQF
∴DE=EF
∵DE⊥EF
∴△DEF是等腰直角三角形
易证△DEC≌△BEC
∴DE=BE
∴EF=BE
∵EQ⊥FB
∴FQ=BQ=BF
∵AB=4,F是AB的中点
∴BF=2
∴FQ=BQ=PE=1
∴CE=,PD=4-1=3
Rt△DAF中,
∴DE=EF=
如图2:∵DC//AB.
∴△DGC∽△FGA
∴
∴AG=2AG,DG=2FG
∴
∵
∴
∴
连接GM、GN,交EF于H.
∵∠GFE=45°
∴△GHF是等腰直角三角形
∴
由折叠得:GM⊥EF,MH=GH=
∴∠EHM=∠DEF=90°
∴DE∥HM
∴△DEN∽△MNH
∴
∴
∴EN=3NH
∵EN+NH=EH=
∴EN=
∴NH=EH-EN=
在Rt△GNH中,
由折叠得:MN=GN,EM=EG
∴△EMN的周长为.
故选:C.
7.如图,在平行四边形中,E是的中点,则下列四个结论:①;②若,,则;③若,则;④若,则与全等.其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】
依次分析各选项,进行推理论证即可;其中①可通过证明,进一步转换后可以得到结论,②可先得到该平行四边形是矩形,利用矩形的性质等得到MN垂直平分BC,即可完成求证,③可以先证明两个三角形的共线边上的高的关系,再利用三角形面积公式即可完成证明,④可以先证明后可进一步证明,即可完成求证.
【详解】
解:∵平行四边形中,E是的中点,
∴,,,
∴,,
∴,
∴,
∴,
故①正确;
若,
则平行四边形是矩形,
由矩形的对角线相等,而点E是矩形的对角线的交点可知,
E点到B、C两点的距离相等,
∴E点在BC的垂直平分线上,
由,可得BN=CN,
所以N点是BC的中点,
∴MN垂直平分BC,
∴,
故②正确;
若,则BN=2CN,
如图1,分别过D、E两点向BC作垂线,垂足分别为Q点和P点,
∵E点是BD中点,
∴DQ=2EP,
∵,
∴,
故③正确;
若,
因为,
所以,
分别过N、C两点向AD作垂线,垂足分别为H、K,
由平行线间的距离处处相等可知:NH=CK,
∴,
∴,
∴,
∴,
又∵,
∴,
故④正确;
故选:D.
8.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形中,点,点,则互异二次函数与正方形有交点时的最大值和最小值分别是( )
A.4,-1 B.,-1 C.4,0 D.,-1
【答案】D
【分析】
分别讨论当对称轴位于y轴左侧、位于y轴与正方形对称轴x=1之间、位于直线x=1和x=2之间、位于直线x=2右侧共四种情况,列出它们有交点时满足的条件,得到关于m的不等式组,求解即可.
【详解】
解:由正方形的性质可知:B(2,2);
若二次函数与正方形有交点,则共有以下四种情况:
当时,则当A点在抛物线上或上方时,它们有交点,此时有,
解得:;
当时,则当C点在抛物线上或下方时,它们有交点,此时有,
解得:;
当时,则当O点位于抛物线上或下方时,它们有交点,此时有,
解得:;
当时,则当O点在抛物线上或下方且B点在抛物线上或上方时,它们才有交点,此时有,
解得:;
综上可得:的最大值和最小值分别是,.
故选:D.
思想方法等.
9.如图,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数 (k>0,x>0)的图象经过点B,则k的值为( )
A. B.8 C.10 D.
【答案】D
【分析】
先由D(-2,3),AD=5,求得A(2,0),即得AO=2;设AD与y轴交于E,求得E(0,1.5),即得EO=1.5;作BF垂直于x轴于F,求证△AOE ∽△CDE,可得,求证△AOE∽△BFA,可得AF=2,BF=,进而可求得B(4,);将B(4,)代入反比例函数,即可求得k的值.
【详解】
解:如图,过D作DH垂直x轴于H,设AD与y轴交于E,过B作BF垂直于x轴于F,
∵点D(-2,3),AD=5,
∴DH=3,
∴,
∴A(2,0),即AO=2,
∵D(-2,3),A(2,0),
∴AD所在直线方程为:,
∴E(0,1.5),即EO=1.5,
∴,
∴ED=AD- AE=5-=,
∵∠AOE=∠CDE,∠AEO=∠CED,
∴△AOE ∽△CDE,
∴,
∴,
∴在矩形ABCD中,,
∵∠EAO+∠BAF=90°,
又∠EAO+∠AEO=90°,
∴∠AEO=∠BAF,
又∵∠AOE=∠BFA,
∴△BFA∽△AOE,
∴,
∴代入数值,可得AF=2,BF=,
∴OF=AF+AO=4,
∴B(4,),
∴将B(4,)代入反比例函数,得,
故选:D.
10.下列各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A.135 B.153 C.169 D.170
【答案】D
【分析】
结合题意,根据数字规律的性质,分别计算正方形中四个数字的规律,即可得到答案.
【详解】
第一个正方形左上角数字为:1
第二个正方形左上角数字为:2
第三个正方形左上角数字为:3
…
第n个正方形左上角数字为:n;
第一个正方形右上角数字为:
第二个正方形右上角数字为:
第三个正方形右上角数字为:
…
第n个正方形右上角数字为:
∵题干中最后一个正方形右上角为:18
∴
∴
∴题干中最后一个正方形为第八个正方形;
第一个正方形左下角数字为:
第二个正方形左下角数字为:
第三个正方形左下角数字为:
…
第n个正方形左下角数字为:
第八个正方形左下角数字为:9;
第一个正方形右下角数字为:
第二个正方形右下角数字为:
第三个正方形右下角数字为:
…
第n个正方形右下角数字为:
∵
∴第8个正方形右下角数字为:
故选:D.
二、填空题
11.将一张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上一点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD,则得下列结论:①△ADF是等边三角形;②tan∠EBF=2﹣;③S△ADF=S正方形ABCD;④BF2=DF•EF.其中正确的是_____.
【答案】①②④.
【分析】
①由正方形的性质得出AB=CD=AD,∠C=∠BAD=∠ADC=90°,∠ABD=∠ADB=45°,由折叠的性质得出MN垂直平分AD,FD=CD,BN=CN,∠FDE=∠CDE,∠DFE=∠C=90°,∠DEF=∠DEC,由线段垂直平分线的性质得出FD=FA,得出△ADF是等边三角形,①正确;
②设AB=AD=BC=4a,则MN=4a,BN=AM=2a,由等边三角形的性质得出∠DAF=∠AFD=∠ADF=60°,FA=AD=4a,FM=AM=2a,得出FN=MN﹣FM=(4﹣2)a,由三角函数的定义即可得出②正确;
③求出△ADF的面积=AD•FM=4a2,正方形ABCD的面积=16a2,得出③错误;
④求出∠BFE=∠DFB,∠BEF=∠DBF,证出△BEF∽△DBF,得出对应边成比例,得出④正确;即可得出结论.
【详解】
解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠C=∠BAD=∠ADC=90°,∠ABD=∠ADB=45°,
由折叠的性质得:MN垂直平分AD,FD=CD,BN=CN,
∠FDE=∠CDE,∠DFE=∠C=90°,∠DEF=∠DEC,
∴FD=FA,
∴AD=FD=FA,即△ADF是等边三角形,①正确;
设AB=AD=BC=4a,则MN=4a,BN=AM=2a,
∵△ADF是等边三角形,
∴∠DAF=∠AFD=∠ADF=60°,FA=AD=4a,FM=AM=2a,
∴FN=MN﹣FM=(4﹣2)a,
∴tan∠EBF=,②正确;
∵△ADF的面积=AD•FM=×4a×2a=4a2,
正方形ABCD的面积=(4a)2=16a2,
∴,③错误;
∵AF=AB,∠BAF=90°﹣60°=30°,
∴∠AFB=∠ABF=75°,
∴∠DBF=75°﹣45°=30°,∠BFE=360°﹣90°﹣60°﹣75°=135°=∠DFB,
∵,
∴=180°﹣15°-135°=30°=∠DBF,
∴△BEF∽△DBF,
∴,∴BF2=DF•EF,④正确;
故答案为:①②④.
12.在中,AB=9,BC=8,∠ABC=60°,⊙A的半径为6,P是上一动点,连接PB,PC,则的最小值_____________的最小值_______
【答案】
【分析】
①连接AP,在AB上取点Q,使AQ=4,连接CQ,利用相似三角形的判定和性质得到,推出,当三点共线时,的值最小,最小值为的长,再利用特殊角的三角函数值以及勾股定理即可求解;
②在AC上取点G,使AG=,连接PG,BG,同①得到当三点共线时,的值最小,最小值为的长,再利用特殊角的三角函数值以及勾股定理即可求解.
【详解】
①连接AP,在AB上取点Q,使AQ=4,连接CQ,
∵⊙A的半径为6,即AP=6,
∴,又,
且,
∴,
∴,
∴,
∴,
当三点共线时,的值最小,最小值为的长,
过C作CI⊥AB于I,
∴,
在Rt△CIB中,∵,BC=8,
,
∴,
∴,
,
在Rt△CIQ中,,
∴的最小值为;
故答案为:;
②连接AP,
由①得:在Rt△CIA中,,
在AC上取点G,使AG=,连接PG,BG,
∴,
∵,
∴,
且,
∴,
∴,
∴,
∴,
当三点共线时,的值最小,最小值为的长,
过G作GH⊥AB于H,
∴,
在Rt△CIA中,,
在Rt△GAH中,
,
∴,
∴,
,
在Rt△GHB中,,
∴的最小值为.
故答案为:.
13.如图,扇形圆心角为,半径为,点,分别为,中点,连接与相交于点,则阴影部分面积为___;
【答案】
【分析】
先求出∠OFA=∠OEB=90°和EG与FG的长,再分别求出扇形面积和空白部分面积,相减即可求解.
【详解】
解:如图,连接EF,
∵点 E , F 分别为 OA , OB 中点,
∴OE=EA=OF=BF=2,
又∵扇形圆心角为 60° ,
∴△OEF是等边三角形,
∴EF=2=EA=BF,∠OEF=∠OFE=60°,
∴∠EAF=∠EFA=∠EBF=∠BEF=30°,
∴∠OFA=∠OEB=90°,
在Rt△AEG和Rt△BFG中,
EG=AE×tan∠EAG=,GF=BF×tan∠GBF=,
连接OG,
则
;
∵扇形面积,
∴阴影面积为:;
故答案为:.
14.如图1是一张双档位可训节靠背椅,档位调节示意图如图2.两脚,以及靠背,座位,其中D,F分别为,上固定连接点,在点A上移动实现靠背的调节,,,已知分米,.
(1)当时,点E离水平地面的离度为_________分米.
(2)当靠背时,有,则的长为_____分米.
【答案】
【分析】
(1)先利用得到,然后证出得到,再用相似三角形的性质得出结果;
(2)作辅助线,然后利用得到,再利用勾股定理求出,利用得出,再利用勾股定理得出结果.
【详解】
(1)如图1,过点作于点,
∵,
∴为的中点,
∵,
∴,
在中,由勾股定理得,
∵,
得,,
过点作延长线作垂线交于点,
∵,
∴,
∵,
∴,
∴,
∵,,
∴,
∴,
∴点E离水平地面的离度为分米;
图1
(2)如图2,过点作,
则,
∵,
∴,
∴,
∵,,
∴,
∴,
过点作于点,
则,
∴,
由勾股定理得:,
∴,
∴,
∵,,,
∴即,
∴,
∴,
∴,
∵,
∴,
∴,
即,
则的长为分米.
图2
15.二次函数y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4),(t,4)三点,当t≥3时,一元二次方程ax2+bx+c=n一定有实数根,则n的取值范围是 ___.
【答案】n≤254
【分析】
根据二次函数y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4),通过列三元一次方程组并求解,即可得到b=a+4及c的值;分a>0和a<0两种情况分析;当a>0时,结合二次函数图像的性质,得t<0,不符合题意;当a<0时,结合二次函数平移和一元二次方程的性质,通过求解二元一次方程组和一元一次方程,即可得到答案.
【详解】
∵y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4)
∴a−b+c=0c=4,
∴b=a+4
根据题意,分a>0和a<0两种情况分析;
当a>0时
∵y=ax2+bx+c(a≠0)的图象经过(﹣1,0),(0,4)
∴y=ax2+bx+c(a≠0)的对称轴x=−b2a<0
∵y=ax2+bx+c(a≠0)的图象经过(0,4),(t,4)
∴0+t2=−b2a<0
∴t<0,即和t≥3相矛盾
∴a>0不符合题意;
当a<0时,y=ax2+bx+c(a≠0)的图象如下图:
当n>0时,y=ax2+bx+c(a≠0)的图象向下平移
∴随n增大,y=ax2+bx+c-n与x轴右侧交点向左移动
根据题意,y=ax2+bx+c-n与x轴右侧交点的最小值,为t=3时,即3,0
∴32=−b2a,即b=−3a
∴b=−3ab=a+4
∴a=−1b=3
∴t=3时,y=ax2+bx+c最大值为254
∴254−n=0
∴n=254
当n<0时,y=ax2+bx+c(a≠0)的图象向上平移;
∴随n减小,y=ax2+bx+c-n与x轴右侧交点向右移动,即当t≥3时,一元二次方程ax2+bx+c=n一定有实数根
∴n≤254
故答案为:n≤254.
16.习近平总书记提出:“绿水青山就是金山银山!”全国上下各行各业都把环境保护放在了首位.重庆某汽车厂在新能汽车的研究上下足功夫,取得了瞩目的成绩!现该汽车厂对一款新车在三条不同的线路上进行测试,每条测试线路都分为高速和非高速两种路段,测试车在出厂时设定了固定不变的高速路段和非高速路段的速度(途中车辆从一种路段变为另一种路段时的加、减速以及车辆出发、停车时的速度变化都忽略不计),其中高速路段车速不低于,非高速路段车速不高于,测试时,测试车都直接从出发地驶向目的地,途中不掉头、不停留.测试记录表上显示,三次测试的时间分别是10小时、16小时、26小时(每条测试线路高速路段和非高速路段各自用去的时间都是整数),并且三条测试线路的路程都是,那么该测试车设定的高速路段速度是______.
【答案】63或72或81.
【分析】
根据题意,找出题目的等量关系,列出方程组,然后解方程组,结合高速路段车速不低于,非高速路段车速不高于,以及时间都是整数,进行讨论分析,即可得到答案.
【详解】
解:设测试车在高速路段上的速度为,则;在低速路段上的速度为,;
测试车三次行驶在高速路段上的时间为:,,;则三次行驶在低速路路段上的时间为:,,,(,,均为整数);则
,
整理得:,
由①②,得:,
由②③,得:,
∵,,均为整数,
∴与成正比例函数,
设
∵,,,,均为整数,
∴,(k只能取正整数)
把代入②,得:,
∴,
∵,
∴,
当时,,此时;
当时,,此时;
当时,,此时或28;
当时,,此时或36;
当时,,此时;
当时,,此时;
当时,,无解;
当时,,不符合题意;
∵,
∴满足题意的有:
①,,此时;
②,,此时;
③,,此时;
∴那么该测试车设定的高速路段速度是:63千米/小时或72千米/小时或81千米/小时;
故答案为:63或72或81.
17.如图,半圆的半径为1,为直径,、为切线,,P为上一动点,求的最小值______________.
【答案】
【分析】
取CO中点M,利用相似三角形的判定和性质推出,利用勾股定理即可计算求解.
【详解】
∵OA=AC=1,AC是切线,
∴∠CAO=90°,
∴CO=,
连接CO、OP,取CO中点M,连接DM,PM,
∴OM=,
∴,∠POM=∠COP,
∴,
∴,
∴,
∴,
过M作MH⊥BD于H,MN⊥AB于N,
∴,MN=,
∴,
∵BD是切线,BD=2,
∴∠ABD=90°,
∴四边形MNBH为矩形,
∴,BH= MN=,
,
∴
∴,即最小值为,
故答案为:.
三、解答题
18.在平面直角坐标系中,O为坐标原点,点A在y轴上,点B在x轴上,∠ABC=90°,AB=BC,连接AC,CD⊥x轴于点D,CD=5.
(1)如图1,求点B的坐标;
(2)如图2,OF平分∠AOB,OF交AC于点F,求证:点F为AC的中点;
(3)如图3,在(2)的条件下,点E在第二象限,连接AE、CE,且∠E=45°,∠ECA+∠BAO=45°,CE=18,求点F的坐标.
【答案】(1)(5,0);(2)见解析;(3)(7,7)
【分析】
(1)由题意易证,即可利用“AAS”证明,即得出,即得出B点坐标.
(2)延长OF、DC,且交于点M,由(1)全等可得,.再根据题意可知,即可证明是等腰直角三角形,即得出,从而可证明BD=CM,即证明出AO=CM.最后利用“ASA”即可证明,得出,即证明F点为AC中点.
(3)如图3-1所示,△ABC是等腰直角三角形,AB=AC,∠BAC=90°,∠BDC=90°,先证明AD平分∠BDC;将沿AC翻折得到,过点N作于点H,过点C作CG⊥EA交EA延长线于G,连接NE,NG,先证明△EGN≌△CGN得到EN=CN, 则,然后利用“AAS”可证明,即得,从而得出,进而可求出,即得出M点坐标.最后由中点坐标公式即可求出F点坐标.
【详解】
解:(1)∵,
∴.
又∵,
∴.
∵轴,
∴,
∴在和中
,
∴,
∴,
∴B点坐标为(5,0).
(2)如图,延长OF、DC,且交于点M,
∵,
∴,.
∵OF平分,
∴,
∵,即,
∴是等腰直角三角形,
∴,
∴,即BD=CM,
∴AO=CM.
∵CD⊥x轴于点D,
∴,
∴,,
∴,
∴,即F点为AC中点.
(3)如图3-1所示,△ABC是等腰直角三角形,AB=AC,∠BAC=90°,∠BDC=90°,现在证明AD平分∠BDC,
将△ABD绕点A逆时针旋转90°得到△ACE,
∴AD=AE,∠DAE=90°,∠ACE=∠ABD,
∵∠BAC=∠BDC=180°,
∴∠ABD+∠ACD=180°,
∴∠ACE+∠ACD=180°,
∴D、C、E三点共线,
∴△ADE是等腰直角三角形,
∴∠ADE=45°,
∴∠ADB=∠BDC-∠ADE=45°,
∴∠ADB=∠ADC,即AD平分∠BDC;
如图3-2所示,将沿AC翻折得到,过点N作于点H,过点C作CG⊥EA交EA延长线于G,连接NE,NG,
∵∠GEC=45°,∠EGC=90°,
∴∠GCE=180°-∠GEC-∠EGC=45°,
∴∠GEC=∠GCE,
∴GE=GC,
∵△ABC中∠ABC=90°,AB=BC,,
∴△ANC中,AN=CN=AB=BC,∠ANC=90°,
∴由前面所证可得∠EGN=∠CGN,
在△EGN和△CGN中,
,
∴△EGN≌△CGN(SAS),
∴EN=CN,
∵NH⊥EC,
∴,
∵,
∴,
∴在和中,
,
∴,
∴,
∴,
∴,
∴点M坐标为(14,14),
∵点F为OM中点,
∴F点坐标为(),即F(),
∴F(7,7).
19.问题发现:
(1)如图①,点A和点B均在⊙O上,且∠AOB=90°,点P和点Q均在射线AM上,若∠APB=45°,则点P与⊙O的位置关系是 ;若∠AQB<45°,则点Q与⊙O的位置关系是 .
问题解决:
如图②、图③所示,四边形ABCD中,AB⊥BC,AD⊥DC,∠DAB=135°,且AB=1,AD=2,点P是BC边上任意一点.
(2)当∠APD=45°时,求BP的长度.
(3)是否存在点P,使得∠APD最大?若存在,请说明理由,并求出BP的长度;若不存在,也请说明理由.
【答案】(1)点P在⊙O上,点Q在⊙O外;(2)PB=2+或;(3)存在,−1
【分析】
(1)如图①中,根据圆周角与圆心角的关系即可判断;
(2)如图2中,造等腰直角三角形△AOD,与O为圆心作⊙O交BC于P、P′,易知∠APD=∠AP′D=45°.求出BP′和BP的长即可解决问题;
(3)作线段AD的垂直平分线,交AD于E,交BC于F,点O在EF上,以OA为半径作⊙O,当⊙O与BC相切于点P时,∠APD最大,求出此时BP的值即可;
【详解】
解:(1)如图①中,
∵∠APB=∠AOB=45°,
∴点P在⊙O上,
∵∠AQB<45°,
∴点Q在⊙O外.
故答案为点P在⊙O上,点Q在⊙O外.
(2)如图2中,如图构造等腰直角三角形△AOD,与O为圆心,OA为半径作⊙O交BC于P、P′,易知∠APD=∠AP′D=45°.
延长DO交BC于H,
∵∠DAB=135°,∠DAO=45°,
∴∠OAB=∠B=90°,
∴OA∥BC,
∴∠DOA=∠OHB=90°,
∴四边形ABHO是矩形,
∴AB=OH=1,OA=BH,
∵AD=2,
∴OA=OD=OP=OP′=2,
在Rt△OPH和Rt△OP′H中,
易知HP=HP′=,
∴BH=OA=2,
∴BP′=2− ,PB=2+.
(3)如图③中,存在.
作线段AD的垂直平分线,交AD于E,交BC于F,点O在EF上,以OA为半径作⊙O,当⊙O与BC相切于点P时,∠APD最大,理由:在BC上任意取一点M,连接MA、MD,MD交⊙O于N,连接AN.
∵∠AND>∠AMD,∠APD=∠AND,
∴∠APD>∠AND,
连接OP,延长DA交CB的延长线于点G.
∵AB⊥BC,∠DAB=135°,
∴∠G=∠EFG=45°,
∴△ABG,△EFG都是等腰直角三角形,
∵AB=BG=1,
∴AG=,
∵AD=2,OE⊥AD,
∴AE=ED=,
∴EG=EF=2,GF=EG=4,
设OP=PF=r,则OF=r,OE=EF−OF=2−r,
在Rt△AOE中,AE2+OE2=OA2,
∴,
解得r=4− 或4+(舍弃),
∴BP=GF−GB−PF=4−1−r=−1.
20.已知等腰直角和等腰直角(),,连接AF,点M是AF的中点,连接MB、ME.
(1)如图,当CB与CE在同一直线上时,
①猜想MB与ME的数量关系和位置关系,
②请证明①的猜想.
(2)若,将绕点C顺时针旋转一周,连接CM,当以点A、B、C、M为项点的四边形是平行四边形时,
①直接写出此时EF的长度.
②直接写出点M到直线EF的距离.
【答案】(1)①,;②见解析;(2)①;②或
【分析】
(1)①据图可推断,;
②先证明,然后证明,然后根据全等三角形的性质可得结论;
(2)①分三种情况,当四边形为平行四边形时,当四边形为平行四边形时,当四边形为平行四边形时,根据情况画出图形,然后进行求值即可;
②根据①的情况,进行分析求解即可.
【详解】
解:①,;
②延长BM与EF相交于点D,
,
;,
是中点,
,
在和中,
,
,
,,
和是等腰三角形,
,,
,
,
在和中,
,
,
,,
,
,
;
(2)①当四边形为平行四边形时,
过点A作交延长线于点,
过作于点,
∵四边形是平行四边形,
∴,
∴,
∵,
∴四边形是正方形,
∴,
∴,
∴,
∵点是的中点,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴是矩形,
∴,
∴
∴,
∵是等腰直角三角形,
∴,
∴;
当四边形为平行四边形时,
,
此时,与题意不符,故舍去;
当四边形为平行四边形时,
,
过作交延长线于,
此时四边形为正方形,
∴
∴,
∴,
∵是等腰直角三角形,
∴,
∴,
∴当为顶点的平行四边形时,的长为;
②当四边形为平行四边形时,
过作交延长线于,
过点作于点,
过点作于点,
由①可知:,
∴,
在和中,
∴,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴是等腰直角三角形,
∴,
由①可知,
∴,
∵,
∴,
∴,
∴,
∴,
即点到直线的距离为;
当四边形是平行四边形时,
过点作交延长线于,
连接,过点作于点,
由①可知为正方形,
∴,
∵,,
∴,
在和中,
,
∴,
∴,
∴,
∴是等腰三角形,
∵,
∴,,
∴,
∴,,
∴,
∴,
∴点M到直线的距离为,
综上所述,点到直线的距离为或.
21.如图,在平面直角坐标系中,的边AB在轴上,且,以AB为直径的圆过点C.若点C的坐标为,,
(1)求抛物线的解析式;
(2)点P为该函数在第一象限内的图象上一点(不与BC重合),过点P作,垂足为点Q,连接PC.若以点P、C、Q为顶点的三角形与相似,求点P的坐标;
(3)若平分线所在的直线l交x轴与点E,过点E任作一直线分别交射线CA,CB(点C除外)于点M,N.则的是否为定值?若是,求出该定值;若不是,请说明理由.
【答案】(1);(2)点P的坐标为:(6,4)或(,);(3),理由见详解.
【分析】
(1)根据题意,先证明∽,得到,求出点A、B的坐标,然后利用待定系数法,即可求出抛物线解析式;
(2)根据题意,可分为两种情况:∽或∽,结合解一元二次方程,相似三角形的判定和性质,分别求出点P的坐标,即可得到答案;
(3)过点E作EI⊥AC于I,EJ⊥CN于J,然后由角平分线的性质定理,得到EI=EJ,再证明△MEI∽△MNC,△NEJ∽△NMC,得到,然后求出EI一个定值,即可进行判断.
【详解】
解:(1)∵以AB为直径的圆过点C,
∴∠ACB=90°,
∵点C的坐标为,
∴CO⊥AB,
∴∠AOC=∠COB=90°,
∴∠ACO+∠OCB=∠ACO+∠OAC=90°,
∴∠OCB=∠OAC,
∴∽,
∴,
∵,,
∴,
∴,
解得:或,
经检验,满足题意,
∵,
∴,
∴点A为(,0),点B为(8,0).
设抛物线的解析式为,把点A、B、C三点的坐标代入,有
,解得:,
∴抛物线的解析式为;
(2)根据题意,如图:
当∽时,
∴,
∵,
∴,
∴PC⊥OC,
∴点P的纵坐标为4,
当时,有,
解得:或(舍去);
∴点P的坐标为(6,4);
当∽时,则此时BC垂直平分OP,作PG⊥y轴,垂足为G,如上图,
∴,
∴AC∥OP,
∴∠ACO=∠POG,
∵,
∴∽,
∴,
设点P为(,),
∴,,
∴,
解得:,
∵点P在第一象限,
∴,
∴,
∴点P的坐标为(,);
综合上述,点P的坐标为:(6,4)或(,);
(3)过点E作EI⊥AC于I,EJ⊥CN于J,如图:
∵CE是∠ACB的角平分线,
∴EI=EJ,
∵EI∥CN,EJ∥CM,
∴△MEI∽△MNC,△NEJ∽△NMC,
∴,,
∴,
∴,
∴,
∵△ACO∽△AEI,
∴,
∵,
∵,
∴,
解得:,经检验,符合题意,
∴;
∴是一个定值.
22.问题背景:已知在中,AB边上的动点D由点A向点B运动(与点A、点B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(点E不与点C重合),连接DE交AC于点F,点H是线段AF上的一点.
(1)初步尝试:如图所示,若是等边三角形,,且点D、点E的运动速度相等,求证:.
(2)类比探究:如图所示,若在中,,,且点D、点E的运动速度之比是,求的值.
(3)延伸拓展.如图所示,若在中,,,记,且点D、点E的运动速度相等,试用含m的代数式表示.
【答案】(1)见解析;(2)2;(3)
【分析】
(1)证法一:过点D作,交AC于点G,由此可以得到是等边三角形,得到,根据三角形全等,可以得到,即可求证;证法二:过点E作交AC的延长线于点M,通过求证三角形全等,即可求解;
(2)方法一:过点D作,交AC于点G,通过全等三角形的性质可求得,即可求解;方法二:过点作,过点作交延长线于点,可以得到为等边三角形,通过三角形全等求得,,即可求解;
(3)方法一:过点D作交AC于点G,通过平行线的性质定理即可求解;方法二:过点作,过点作交延长线于点,根据相似三角形的性质求得,即可求解.
【详解】
解:(1)证明:证法一 如图所示,过点D作,交AC于点G.
是等边三角形,
,,
是等边三角形,
.
,.
又,
,,
易证.
,
,即.
证法二 如图所示,过点E作交AC的延长线于点M.
是等边三角形,
.
,,
.
,
,
,.
又∵,,
,
.
(2)方法一:如图所示,过点D作,交AC于点G,则.
,
.
,.
由题意可知,,
.
,
,,
,
,
,即,
.
方法二:过点作,过点作交延长线于点,如下图:
由题意得,,
∴,,
∴,即为等边三角形
∴
在中,,由勾股定理可以求得,即
∴
又∵,
∴
∴
∴
∴
(3)如图所示,过点D作交AC于点G,可得,,.
.
又,
,
.
由比例的性质可得,,
,
,即.
方法二:过点作,过点作交延长线于点,如下图:
∵
∴,
∴,
∴
∴
∵
∴,
∴
又∵
∴
∴
由题意可得,,∴,
∴
又∵
∴
23.在平面直角坐标系中,点O为坐标原点,抛物线交x轴的负半轴于点A,交x轴的正半轴点B,交y轴的正半轴于点C,且OB=2OC.
(1)求a的值;
(2)如图1,点D、P分别在一、三象限的抛物线上,其中点P的横坐标为t,连接BP,交y轴于点E,连接CD、DE,设△CDE的面积为s,若,求点D的坐标;
(3)如图2,在(2)的条件下,将线段DE绕点D逆时针旋转90°得到线段DF,射线AE与射线FB交于点G,连接AP,若∠AGB=2∠APB,求点P的坐标.
【答案】(1);(2);(3)
【分析】
(1)根据已知条件求得点坐标,进而求得的长,将解析式变形为,进而求得的坐标,求得的长,根据,即可求得的值,进而求得解析式;
(2)根据已知二次函数解析式,由已知条件可得点P的横坐标为t,则设的横坐标为,设直线的解析式为,根据的坐标,的坐标,求得直线解析,进而求得点的坐标,求得△CDE的面积,根据已知条件,进而求得的横坐标,将横坐标代入二次函数解析式,即可求得的坐标;
(3)连接,过作轴与,根据已知条件求得是等腰直角三角形,根据旋转证明,延长至,使得,连接,证明,是等腰直角三角形,根据已知条件∠AGB=2∠APB可推出,过点引坐标的两条垂线,垂足为,作直线关于轴对称的直线,交于点,过点作,证明,根据,根据(2)的结论,求得的坐标,进而求得根据的坐标和的坐标,求得列出比例式,解方程即可求得的值,进而求得的坐标.
【详解】
(1)抛物线交x轴的负半轴于点A,交x轴的正半轴点B,交y轴的正半轴于点C,且,
令,则,则,
,
由,
则,,
,
,
即,
解得,
(2),
,
点P的横坐标为t,则,,,,
设的横坐标为,
设直线的解析式为,
则
解得
,
,
,
设△CDE的面积为s,
则,
,
,
解得,
,
将代入,
,
(3)如图,连接,过作轴与
,,,,,
,
,
是等腰直角三角形
将线段DE绕点D逆时针旋转90°得到线段DF,
,
,
延长至,使得,连接,
,
在与中
,,
即
是等腰直角三角形
过点引坐标的两条垂线,垂足为,作直线关于轴对称的直线,交于点,过点作,设关于轴对称的点为,
设,则,,
轴,是等腰直角三角形,
,
,轴,
,的横坐标为1,
直线的解析式为
令
解得
,
,,
,,
,
即,
整理得,
解得,
,
,
将代入,
.
24.已知△AOB和△MON都是等腰直角三角形(OA<ON<OA),∠AOB=∠MON=90°.
(1)如图1:连AM,BN,求证:△AOM≌△BON;
(2)若将△MON绕点O顺时针旋转;
①如图2,当点N恰好在AB边上时,求证:BN2+AN2=2ON2;
②填空:当点A,M,N在同一条直线上时,若OB=4,ON=3,BN= .
【答案】(1)证明见解析;(2)①证明见解析;②或
【分析】
(1)根据等腰直角三角形的性质,得,,;再根据全等三角形的判定性质分析,即可得到答案;
(2)①连接,通过证明△AOM≌△BON,得,;根据等腰直角三角形,推导得,根据勾股定理,得、,即可完成证明;
②结合题意,根据旋转的性质,分点在右侧和点在左侧两种情况分析;当点在右侧时,结合(1)的结论,根据等腰直角三角形、全等三角形的性质,得,再根据勾股定理和二次根式的性质,通过列一元二次方程并求解,即可得到答案;当在左侧时,同理,通过计算即可得到答案.
【详解】
(1)∵△AOB和△MON都是等腰直角三角形
∴,
∵∠AOB=∠MON=90°
∴,即
∴△AOM和△BON中
∴△AOM≌△BON;
(2)①连接,如下图
∵∠AOB=∠MON=90°
∴,即
∴△AOM和△BON中
∴△AOM≌△BON;
∴,
∵,∠AOB=90°
∴
∴
∴
∴
∵,∠MON=90°
∴
∴BN2+AN2=2ON2;
②根据题意,分两种情况分析
当点在右侧时,如下图,分别连接、,过点作,交于点
∵∠AOB=∠MON=90°
∴,即
∴△AOM和△BON中
∴△AOM≌△BON;
∴
∵,,∠AOB=∠MON=90°
∴,
∴
∵
∴
直角中,
∴
∴或(舍去)
∴;
当点在左侧时,如下图,分别连接、,过点作,交于点
∵∠AOB=∠MON=90°
∴,即
∴△AOM和△BON中
∴△AOM≌△BON;
∴
∵,,∠AOB=∠MON=90°
∴,
∴
∵
∴
直角中,
直角中,
∴
∴或(舍去)
∴ ;
∴
故答案为:或.
25.如图1,直线y=x-5与x轴、y轴分别交于B、C两点,点A为y轴正半轴上一点,且=75.
(1)请直接写出点B、C的坐标及直线AB的解析式: 、 、 ;
(2)如图2,点P为线段OB上一点,若∠BCP=45°,请写出点P的坐标: ,并简要写出解答过程;
(3)如图3,点D是AB的中点,M是OA上一点,连接DM,过点D作DN⊥DM交OB于点N,连接BM,若∠OBM=2∠ADM,请写出点M的坐标 ,并简要写出解答过程.
【答案】(1),;(2);(3)
【分析】
(1)分别令进而求得直线与坐标轴的交点,根据已知条件待定系数法求解析式即可;
(2)过点作于点,过点作轴,过分别作平行于轴,交于点,证明,可得,根据图形与坐标的关系,即可求得,设直线的直线解析式为,待定系数法求解析式即可,令,进而求得点的坐标;
(3)连接,证明是等腰直角三角形,设交于点,设,则过点作轴,作的角平分线交于点,过点作分别垂直于,垂足分别为,连接,证明,,进而证明,设,则在中,,勾股定理列出方程,求得,进而求得,从而求得的坐标.
【详解】
(1)直线y=x-5与x轴、y轴分别交于B、C两点,
令,则,令,则,
点A为y轴正半轴上一点,
设直线AB的解析式为,将,代入,得
解得
直线AB的解析式为
故答案为:,
(2)如图,过点作于点,过点作轴,过分别作平行于轴,交于点,
是等腰直角三角形
,
轴,轴,轴,
,
在与中
,
设直线的直线解析式为,将,代入,则
解得
直线的直线解析式为
令,则
即
故答案为:
(3)如图, 连接,
,
是等腰直角三角形
点是的中点,
,
,,
是等腰直角三角形,
设交于点,设,则
,
过点作轴,作的角平分线交于点,过点作分别垂直于,垂足分别为,连接,如图,
,平分
,
又
四边形是正方形
在与中
,
在和中
设,则
,
在中,
即
整理得
即
解得(舍)
2022-2023 数学京改版新中考精讲精练 中考模拟卷(二): 这是一份2022-2023 数学京改版新中考精讲精练 中考模拟卷(二),文件包含2022-2023数学京改版新中考精讲精练中考模拟卷二解析版docx、2022-2023数学京改版新中考精讲精练中考模拟卷二原卷版docx等2份试卷配套教学资源,其中试卷共55页, 欢迎下载使用。
2022-2023 数学京改版新中考精讲精练 中考模拟卷(一): 这是一份2022-2023 数学京改版新中考精讲精练 中考模拟卷(一),文件包含2022-2023数学京改版新中考精讲精练中考模拟卷一解析版docx、2022-2023数学京改版新中考精讲精练中考模拟卷一原卷版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
2022-2023 数学京改版新中考精讲精练 考点30概率及有关计算: 这是一份2022-2023 数学京改版新中考精讲精练 考点30概率及有关计算,文件包含2022-2023数学京改版新中考精讲精练考点30概率及有关计算解析版docx、2022-2023数学京改版新中考精讲精练考点30概率及有关计算原卷版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












