

七年级数学下册考点精练专题18 多乘多与图形面积
展开
这是一份七年级数学下册考点精练专题18 多乘多与图形面积,共38页。
专题18 多乘多与图形面积
【例题讲解】
如图,有足够多的边长为的小正方形(类),长为、宽为的长方形(类)及边长为的大正方形(类). 发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为.
(1)取图①中的若干个(三种材料都要取到)拼成一个长方形,使其面积为,画出图形,并根据图形回答:______________.
(2)若取其中的若干个(三种材料都要取到)拼成一个长方形,使其面积为,
①你画的图中需类卡片___________张;②可将多项式分解因式为_____________;
(3)如图③,大正方形的边长为,小正方形的边长为.若用表示四个相同的长方形的两边长,观察图形并判断下列关系式:①;②;③;④,其中正确的是____________.
【详解】(1)解:拼图如图所示:
所以(2a+b)(a+2b)=2a2+5ab+2b2,
故答案为:2a2+5ab+2b2;
(2)①a2+5ab+6b2即用A型的1张,B型的5张,C型的6张,
故答案为:6 可以拼成如图所示的图形,
因此可得等式:a2+5ab+6b2=(a+3b)(a+2b),
故答案为:a2+5ab+6b2=(a+3b)(a+2b);
(3)由图③可知,m=x+y,n=x-y,故②符合题意;
因此有m+n=2x,m-n=2y,
故①符合题意;
mn=(x+y)(x-y)=x2-y2;故③不符合题意;
故④不符合题意;故答案为:①②.
【综合解答】
1.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式( )
A.(a+b)(a+2b)=a2+3ab+2b2
B.(a+b)(2a+b)=2a2+3ab+b2
C.(a+b)(a+2b)=2a2+3ab+b2
D.(a+b(2a+b)=a2+3ab+2b2
2.如图,在长为,宽为的长方形铁片上,挖去长为,宽为b的小长方形铁片,则剩余部分面积是( )
A. B. C. D.
3.如图,请根据图中标的数据,计算大长方形的面积.通过面积不同的计算方法,可以得到的等式关系是:_____.
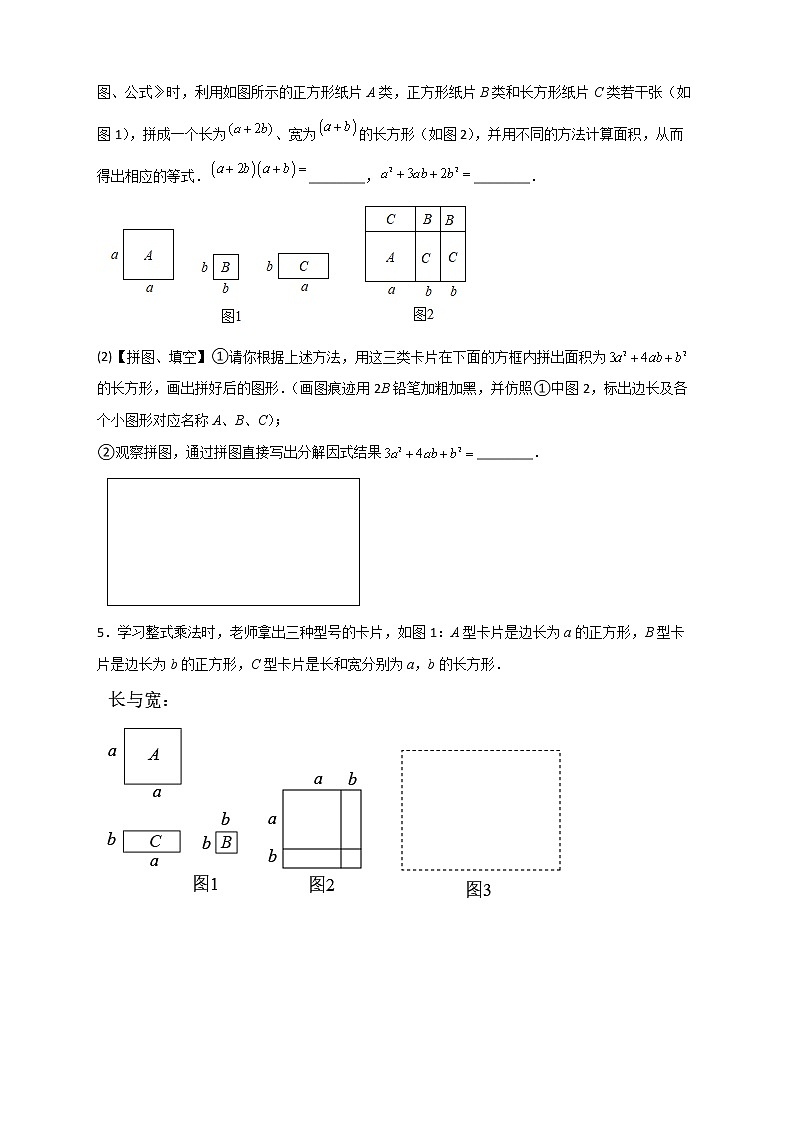
4.(1)【观察、填空】七(1)班数学学习兴趣小组的同学在研究课本第九章的“数学活动”《拼图、公式》时,利用如图所示的正方形纸片A类,正方形纸片B类和长方形纸片C类若干张(如图1),拼成一个长为、宽为的长方形(如图2),并用不同的方法计算面积,从而得出相应的等式.________,________.
(2)【拼图、填空】①请你根据上述方法,用这三类卡片在下面的方框内拼出面积为的长方形,画出拼好后的图形.(画图痕迹用2B铅笔加粗加黑,并仿照①中图2,标出边长及各个小图形对应名称A、B、C);
②观察拼图,通过拼图直接写出分解因式结果________.
5.学习整式乘法时,老师拿出三种型号的卡片,如图1:A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形.
(1)选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个长为的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式____________;
(2)请用这3种卡片拼出一个面积为的长方形(数量不限),在图3的虚线框中画出示意图,并在示意图上按照图2的方式标注好长方形的长与宽;
(3)选取1张A型卡片,4张C型卡片按图4的方式不重叠地放在长方形DEFG框架内,图中两阴影部分(长方形)为没有放置卡片的部分.已知GF的长度固定不变,DG的长度可以变化,图中两阴影部分(长方形)的面积分别表示为,.若,则当a与b满足____时,S为定值,且定值为______.(用含b的代数式表示)
6.将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形,1号正方形的边长为x,2号正方形的边长为y.
(1)求5号长方形的面积(用含x,y的代数式表示);
(2)若图1中长方形的周长为24.
①若2号正方形与1号正方形的面积差为3,求5号长方形的面积;
②将图1中的1号、2号、3号、4号四个正方形和5号长方形按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为________.
7.提出问题:怎么运用矩形面积表示(y+2)(y+3)与2y+5的大小关系(其中y>0)?
几何建模:
(1)画长y+3,宽y+2的矩形,按图方式分割
(2)变形:2y+5=(y+2)+(y+3)
(3)分析:图中大矩形的面积可以表示为(y+2)(y+3);阴影部分面积可以表示为(y+3)×1,画点部分的面积可表示为y+2,由图形的部分与整体的关系可知:
(y+2)(y+3)>(y+2)+(y+3),即(y+2)(y+3)>2y+5
归纳提炼:
当a>2,b>2时,表示ab与a+b的大小关系.根据题意,设a=2+m,b=2+n(m>0,n>0),要求参照上述研究方法,画出示意图,并写出几何建模步骤(用铅笔画图,并标注相关线段的长)
8.(1)探究:我们小学时学过乘法分配律a(b+c)=ab+ac.
下面我们用等积法证明乘法分配律:
如图,方法一:长方形ABCD的一边长为a,另一边长为(b+c),所以长方形ABCD的面积为a(b+c);
方法二,长方形ABFE的面积为ab,长方形CDEF的面积为ac,所以长方形ABCD的面积为(ab+ac),所以a(b+c)=ab+ac.
我们把这种用两种不同的方式表示同一图形面积的方法称为等积法.
(2)应用
请你用等积法,画出图形,并仿照上面的说理方法证明:(a+b)(c+d)=ac+ad+bc+bd;
(3)拓展
请直接写出(a+b)(c+d+e)= .
9.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式,例如图1可以得到,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:____________________;
(2)利用(1)中得到的结论,解决下面的问题:若,,求的值;
(3)小明同学用图3中张边长为的正方形,张边长为的正方形,张宽、长分别为a,b的长方形纸片拼出一个面积为长方形,请画出图形并根据图形回答:__________;
(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:__________.
10.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若,,则 .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+2y+z= .
(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
11.数学活动
活动材料现有若干块如图①所示的正方形和长方形硬纸片.
活动要求用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,探求相应的等式.
例如,由图②,我们有或.
问题:(1)选取正方形、长方形硬纸片共8块,拼出一个如图③的长方形,计算它的面积,并写出相应的等式;
(2)试借助拼图的方法,把二次三项式分解因式,并把所拼的图形画在虚线方框内.
(3)将分解因式(直接写出结果,不需要画图).
12.学习整式乘法时,老师拿出三种型号的卡片,如图1;型卡片是边长为的正方形,型卡片是边长为的正方形,型卡片是长和宽分别为,的长方形.
(1)选取1张型卡片,2张型卡片,1张型卡片,在纸上按照图2的方式拼成一个长为的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式_______;
(2)请用这3种卡片拼出一个面积为的长方形(数量不限),在图3的虚线框中画出示意图,并在示意图上按照图2的方式标注好长方形的长与宽;
(3)选取1张型卡片,4张型卡片按图4的方式不重叠地放在长方形框架内,图中两阴影部分(长方形)为没有放置卡片的部分,已知的长度固定不变,的长度可以变化,图中两阴影部分(长方形)的面积分别表示为,.若,则当与满足______时,为定值,且定值为________.(用含或的代数式表示)
13.【活动材料】若干个如图1所示的长方形和正方形硬纸片
【活动要求】用若干块这样的长方形和正方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,探求相应的等式.
例如,由图2,我们可以得到,
或.
【问题解决】
(1)选取正方形、长方形硬纸片共8块,拼出如图3的长方形,直接写出相应的等式______;
(2)尝试借助拼图的方法,把二次三项式分解因式,并把所拼的图形画在图4的虚线方框内.
(3)将分解因式:______(直接写出结果,不需要画图).
14.把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式 ;
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长为a、b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若这两个正方形的边长a、b如图标注,且满足a+b=10,ab=20.请求出阴影部分的面积.
(4)图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片,现有足量的这三种纸片.
①请在下面的方框中用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,并仿照图1、图2画出拼法并标注a、b;
②研究①拼图发现,可以分解因式2a2+5ab+2b2= .
15.一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示 块, 块, 块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个小长方形的两边长(x>y),观察图案,以下关系式正确的是 (填序号).
①,②,③,④
16.一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.
17.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
(1)根据如图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用如图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(4)两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如图4.请你根据如图中图形的关系,写出一个代数恒等式,并写出推导过程.
18.当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如:由图①,可得等式(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式_________________________________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多)画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)小明用2张边长为a的正方形、3张边长为b的正方形、5张邻边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为____________.
19.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请回答下列问题:
(1)写出图2中所表示的数学等式:_____________.
(2)利用(1)中所得的结论,解决下列问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个长为b、宽为a的长方形纸片.
①请按要求利用所给的纸片拼出一个几何图形,并画在所给的方框内,要求所拼的几何图形的面积为2a2+5ab+2b2;
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式,即2a2+5ab+2b2=________.
专题18 多乘多与图形面积
【例题讲解】
如图,有足够多的边长为的小正方形(类),长为、宽为的长方形(类)及边长为的大正方形(类). 发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为.
(1)取图①中的若干个(三种材料都要取到)拼成一个长方形,使其面积为,画出图形,并根据图形回答:______________.
(2)若取其中的若干个(三种材料都要取到)拼成一个长方形,使其面积为,
①你画的图中需类卡片___________张;②可将多项式分解因式为_____________;
(3)如图③,大正方形的边长为,小正方形的边长为.若用表示四个相同的长方形的两边长,观察图形并判断下列关系式:①;②;③;④,其中正确的是____________.
【详解】(1)解:拼图如图所示:
所以(2a+b)(a+2b)=2a2+5ab+2b2,
故答案为:2a2+5ab+2b2;
(2)①a2+5ab+6b2即用A型的1张,B型的5张,C型的6张,
故答案为:6 可以拼成如图所示的图形,
因此可得等式:a2+5ab+6b2=(a+3b)(a+2b),
故答案为:a2+5ab+6b2=(a+3b)(a+2b);
(3)由图③可知,m=x+y,n=x-y,故②符合题意;
因此有m+n=2x,m-n=2y,
故①符合题意;
mn=(x+y)(x-y)=x2-y2;故③不符合题意;
故④不符合题意;故答案为:①②.
【综合解答】
1.观察图形,用两种不同的方法计算大长方形面积,我们可以验证等式( )
A.(a+b)(a+2b)=a2+3ab+2b2
B.(a+b)(2a+b)=2a2+3ab+b2
C.(a+b)(a+2b)=2a2+3ab+b2
D.(a+b(2a+b)=a2+3ab+2b2
【答案】A
【分析】根据图形,大长方形面积等于三个小正方形面积加上三个小长方形的面积和,列出等式即可.
【详解】解:∵长方形的面积=(a+b)(a+2b)
长方形的面积=a2+ab+ab+ab+b2+b2= a2+3ab+2b2,
∴(a+b)(a+2b)= a2+3ab+2b2
故选:A.
【点睛】本题考查多项式乘以多项式的几何意义,通过几何图形之间的数量关系对多项式乘以多项式做出几何解释.
2.如图,在长为,宽为的长方形铁片上,挖去长为,宽为b的小长方形铁片,则剩余部分面积是( )
A. B. C. D.
【答案】B
【分析】根据长方形的面积公式分别计算出大长方形、小长方形的面积,再进行相减即可得出答案.
【详解】解:
,
故剩余部分面积是,
故选B.
【点睛】本题考查了多项式乘多项式、整式的混合运算,解题的关键是掌握长方形的面积公式.
3.如图,请根据图中标的数据,计算大长方形的面积.通过面积不同的计算方法,可以得到的等式关系是:_____.
【答案】
【分析】先利用长乘以宽表示大长方形的面积,再利用3个边长为a的小正方形、2个边长为b的小正方形、5个长宽分别为b和a的长方形面积和表示即可得到等式.
【详解】解:长方形的面积可以表示为,
长方形的面积还可以表示为,
∴.
故答案为:.
【点睛】本题考查了用代数式表示图形的面积,解题关键是理解整体与局部的关系,即局部面积之和等于整体面积.
4.(1)【观察、填空】七(1)班数学学习兴趣小组的同学在研究课本第九章的“数学活动”《拼图、公式》时,利用如图所示的正方形纸片A类,正方形纸片B类和长方形纸片C类若干张(如图1),拼成一个长为、宽为的长方形(如图2),并用不同的方法计算面积,从而得出相应的等式.________,________.
(2)【拼图、填空】①请你根据上述方法,用这三类卡片在下面的方框内拼出面积为的长方形,画出拼好后的图形.(画图痕迹用2B铅笔加粗加黑,并仿照①中图2,标出边长及各个小图形对应名称A、B、C);
②观察拼图,通过拼图直接写出分解因式结果________.
【答案】(1)
(2)①见解析;②
【分析】(1)根据长方形的面积公式可以写出长方形的面积,六个图形的面积之和也等于长方形的面积,即可得出答案;
(2)①根据为3个边长为a的正方形、4个长方形和1个边长为b的正方形的面积之和,用这些图形拼成一个大长方形即可;
②根据拼成的长方形的长和宽表示出长方形的面积,即可得出结果.
(1)
解:∵大长方形由1个正方形A、三个长方形C和2个正方形B组成,
∴大长方形的面积为:,
∴;
.
故答案为:;.
(2)
∵大长方形的面积为,
∴大长方形由3个A,4个C和1个B组成,如图所示:
②根据上图可知,大长方形的长为,宽为,面积为,
∴.
故答案为:①见解析;②.
【点睛】本题主要考查了用图形法分解因式,根据示例和多项式的特点构建几何图形,拼接大长方形是解题的关键.
5.学习整式乘法时,老师拿出三种型号的卡片,如图1:A型卡片是边长为a的正方形,B型卡片是边长为b的正方形,C型卡片是长和宽分别为a,b的长方形.
(1)选取1张A型卡片,2张C型卡片,1张B型卡片,在纸上按照图2的方式拼成一个长为的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式____________;
(2)请用这3种卡片拼出一个面积为的长方形(数量不限),在图3的虚线框中画出示意图,并在示意图上按照图2的方式标注好长方形的长与宽;
(3)选取1张A型卡片,4张C型卡片按图4的方式不重叠地放在长方形DEFG框架内,图中两阴影部分(长方形)为没有放置卡片的部分.已知GF的长度固定不变,DG的长度可以变化,图中两阴影部分(长方形)的面积分别表示为,.若,则当a与b满足____时,S为定值,且定值为______.(用含b的代数式表示)
【答案】(1)=
(2)见解析
(3)时,
【分析】(1)用两种方法表示图2的面积,即可得出公式;
(2)由a2+4ab+3b2可得A型卡片1张,B型卡片3张,C型卡片4张,根据题意画出图形即可;
(3)设DG的长为x,求出S1,S2即可解决问题.
(1)
解:方法1:大正方形的面积为(a+b)2,
方法2:图中四部分的面积和为a2+2ab+b2,
∴(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)
解:如图3,
(3)
解:设DG的长为x,
∵S1=a[x-(a+2b)]=ax-a2-2ab,S2=2b(x-a)=2bx-2ab,
∴S=S2-S1
=2bx-2ab-(ax-a2-2ab)
=(2b-a)x+a2,
若S为定值,则2b-a=0,
∴a=2b,
∴当a与b满足a=2b时,S为定值,且定值为,
故答案为:a=2b,.
【点睛】本题考查了完全平方公式,完全平方公式的几何背景,掌握完全平方公式的特点,数形结合的数学思想是解决问题的关键.
6.将图1中的长方形纸片剪成1号、2号、3号、4号四个正方形和5号长方形,1号正方形的边长为x,2号正方形的边长为y.
(1)求5号长方形的面积(用含x,y的代数式表示);
(2)若图1中长方形的周长为24.
①若2号正方形与1号正方形的面积差为3,求5号长方形的面积;
②将图1中的1号、2号、3号、4号四个正方形和5号长方形按图2的方式放入周长为40的长方形中,则没有覆盖的阴影部分的周长为________.
【答案】(1)
(2)①;②34
【分析】(1)表示出5号长方形的长和宽即可;
(2)①根据2号正方形与1号正方形的面积差为3,以及图1中长方形的周长为24可以列方程求出x、y的值,代入第(1)问式子中计算即可;
②表示出阴影部分周长,最后整体代入求值即可
(1)
由图形可知:
3号正方形的边长为:,
4号正方形的边长为:
5号长方形的长为:,宽为:
∴5号长方形的面积为:
(2)
①∵长方形的长为:,宽为:
又长方形的周长为24,
∴,
∴
∵2号正方形与1号正方形的面积差为3,
∴,
∴
∵,
∴,
∴
把代入得5号长方形的面积为5
②∵图1中长方形的周长为24
∴,
∴
如图,可得:没有覆盖的阴影部分的周长为四边形ABCD的周长,
∵
且图2的大长方形周长为40,
∴,
∴
∴四边形ABCD的周长为
【点睛】本题考查整式加减的应用,设出未知数,列代数式表示各线段进而解决问题是关键.
7.提出问题:怎么运用矩形面积表示(y+2)(y+3)与2y+5的大小关系(其中y>0)?
几何建模:
(1)画长y+3,宽y+2的矩形,按图方式分割
(2)变形:2y+5=(y+2)+(y+3)
(3)分析:图中大矩形的面积可以表示为(y+2)(y+3);阴影部分面积可以表示为(y+3)×1,画点部分的面积可表示为y+2,由图形的部分与整体的关系可知:
(y+2)(y+3)>(y+2)+(y+3),即(y+2)(y+3)>2y+5
归纳提炼:
当a>2,b>2时,表示ab与a+b的大小关系.根据题意,设a=2+m,b=2+n(m>0,n>0),要求参照上述研究方法,画出示意图,并写出几何建模步骤(用铅笔画图,并标注相关线段的长)
【答案】ab>a+b.见解析
【分析】画长为2+m,宽为2+n的矩形,并按图方式分割.图中大矩形面积可表示为(2+m)(2+n),阴影部分面积可表示为2+m与2+n的和.由图形的部分与整体的关系可知ab>a+b.
【详解】解:(1)画长为2+m,宽为2+n的矩形,并按图方式分割.
(2)变形:a+b=(2+m)+(2+n)
(3)分析:图中大矩形面积可表示为(2+m)(2+n);阴影部分面积可表示为2+m与2+n的和.由图形的部分与整体的关系可知,(2+m)(2+n)>(2+m)+(2+n),即ab>a+b.
【点睛】本题主要考查了作图-应用与设计作图及整式的混合运算,解题的关键是利用数形结合思想建立了代数(速算、方程与不等式等)与几何图形之间的内在联系.
8.(1)探究:我们小学时学过乘法分配律a(b+c)=ab+ac.
下面我们用等积法证明乘法分配律:
如图,方法一:长方形ABCD的一边长为a,另一边长为(b+c),所以长方形ABCD的面积为a(b+c);
方法二,长方形ABFE的面积为ab,长方形CDEF的面积为ac,所以长方形ABCD的面积为(ab+ac),所以a(b+c)=ab+ac.
我们把这种用两种不同的方式表示同一图形面积的方法称为等积法.
(2)应用
请你用等积法,画出图形,并仿照上面的说理方法证明:(a+b)(c+d)=ac+ad+bc+bd;
(3)拓展
请直接写出(a+b)(c+d+e)= .
【答案】(2)证明见解析;(3)
【分析】(2)画出图形,并仿照(1)的说理方法证明即可;
(3)根据(1)的方法画出图形,进行计算即可.
【详解】(2)如图,
方法一:长方形ABCD的一边长为,另一边长为,所以长方形ABCD的面积为;
方法二,长方形AGOE的面积为,长方形EODH的面积为,长方形GOFB的面积为,长方形OFCH的面积为,
所以长方形ABCD的面积为(),所以.
(3)如图,
同理可得:方法一可得长方形ABCD的面积为,
方法二可得长方形ABCD的面积为
故答案为:
【点睛】本题考查了多项式乘法与图形面积的关系,数形结合是解题的关键.
9.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式,例如图1可以得到,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:____________________;
(2)利用(1)中得到的结论,解决下面的问题:若,,求的值;
(3)小明同学用图3中张边长为的正方形,张边长为的正方形,张宽、长分别为a,b的长方形纸片拼出一个面积为长方形,请画出图形并根据图形回答:__________;
(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:__________.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)30;(3)9;(4)x3−x=(x+1)(x−1)x
【分析】(1)依据正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,可得等式;
(2)依据(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,进行计算即可;
(3)依据画出图形,即可得到x,y,z的值,进而即可求解;
(4)根据原几何体的体积=新几何体的体积,列式可得结论.
【详解】解:(1)由图2得:正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∵,,
∴102=a2+b2+c2+2×35,
∴a2+b2+c2=100−70=30;
(3)如图所示:
∴x=2,y=2,z=5,
∴x+y+z=9,
故答案为:9;
(4)∵原几何体的体积=x3−1×1•x=x3−x,新几何体的体积=(x+1)(x−1)x,
∴x3−x=(x+1)(x−1)x.
故答案为:x3−x=(x+1)(x−1)x.
【点睛】本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.
10.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若,,则 .
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+2y+z= .
(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式: .
【答案】(1);(2)30;(3)11;(4)
【分析】(1)依据正方形的面积=(a+b+c)2;正方形的面积=a2+b2+c2+2ab+2ac+2bc,可得等式;
(2)依据a2+b2+c2=(a+b+c)2-2ab-2ac-2bc,进行计算即可;
(3)依据所拼图形的面积为:xa2+yb2+zab,而(2a+b)(a+2b)=2a2+4ab+ab+2b2=2a2+5b2+2ab,即可得到x,y,z的值.
(4)根据原几何体的体积=新几何体的体积,列式可得结论.
【详解】解:(1)由图2得:正方形的面积可表示为(a+b+c)2,
正方形的面积也可表示为a2+b2+c2+2ab+2ac+2bc,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∵a+b+c=10,ab+ac+bc=35,
∴102=a2+b2+c2+2×35,
∴a2+b2+c2=100-70=30,
故答案为:30;
(3)由题意得:(2a+b)(a+2b)=xa2+yb2+zab,
∴2a2+5ab+2b2=xa2+yb2+zab,
∴x=2,y=2,z=5,
∴x+2y+z=11,
故答案为:11;
(4)∵原几何体的体积=x3-1×1•x=x3-x,
新几何体的体积=(x+1)(x-1)x,
∴x3-x= x (x+1)(x-1).
故答案为:x3-x= x (x+1)(x-1).
【点睛】本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的体积或面积,然后根据它们的体积或面积相等列出等式是解题的关键.
11.数学活动
活动材料现有若干块如图①所示的正方形和长方形硬纸片.
活动要求用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,探求相应的等式.
例如,由图②,我们有或.
问题:(1)选取正方形、长方形硬纸片共8块,拼出一个如图③的长方形,计算它的面积,并写出相应的等式;
(2)试借助拼图的方法,把二次三项式分解因式,并把所拼的图形画在虚线方框内.
(3)将分解因式(直接写出结果,不需要画图).
【答案】(1),或;(2),作图见解析;(3).
【分析】(1) 根据图形分析,正方形、长方形硬纸片8块拼成了一个大长方形的面积,利用面积相等即可求得等式;
(2)根据题意得这个图形有6块纸片构成,2个小正方形,1个大正方形,3个长方形,拼成一个大长方形,画出长方形即可;
(3)依据代数式画出图形,注意式子中有一个减号,所以拼出来的图形是一个长方形,减去了一部分,然后根据图形可以分解因式.
【详解】解:(1)由图③的,共有8块硬纸片拼成,其中1个小正方形,3个大正方形,4个长方形,所以面积为:,
∴或;
(2),
所拼图形如图:
;
(3)如图,可拼图如下,
∴
【点睛】本题考查了通过图形拼凑进行代数式的运算或因式分解,正确拼出图形,采用数形结合理解几何图形面积的意义是解题关键.
12.学习整式乘法时,老师拿出三种型号的卡片,如图1;型卡片是边长为的正方形,型卡片是边长为的正方形,型卡片是长和宽分别为,的长方形.
(1)选取1张型卡片,2张型卡片,1张型卡片,在纸上按照图2的方式拼成一个长为的大正方形,通过不同方式表示大正方形的面积,可得到乘法公式_______;
(2)请用这3种卡片拼出一个面积为的长方形(数量不限),在图3的虚线框中画出示意图,并在示意图上按照图2的方式标注好长方形的长与宽;
(3)选取1张型卡片,4张型卡片按图4的方式不重叠地放在长方形框架内,图中两阴影部分(长方形)为没有放置卡片的部分,已知的长度固定不变,的长度可以变化,图中两阴影部分(长方形)的面积分别表示为,.若,则当与满足______时,为定值,且定值为________.(用含或的代数式表示)
【答案】(1)=;(2)见解析;(3);.
【分析】(1)从个体和从整体两个方面计算大正方形的面积即可解题;
(2)利用因式分解将化为,结合长方形面积公式画图;
(3)设DG=x,结合图形,计算的值得到S的表达式,根据S为定值,与x的值无关解题.
【详解】解:(1)从个体看:大正方形面积为,从整体看,大正方形面积为,
故得到乘法公式:=,
故答案为:=;
(2)根据长方形面积公式画图如下:
;
(3)设DG=x,由图可知
,
若为定值,则S将不随x的变化而变化,
即,
,
此时
故答案为:;.
【点睛】本题考查完全平方公式的几何背景,是重要考点,难度一般,掌握相关知识是解题关键.
13.【活动材料】若干个如图1所示的长方形和正方形硬纸片
【活动要求】用若干块这样的长方形和正方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,探求相应的等式.
例如,由图2,我们可以得到,
或.
【问题解决】
(1)选取正方形、长方形硬纸片共8块,拼出如图3的长方形,直接写出相应的等式______;
(2)尝试借助拼图的方法,把二次三项式分解因式,并把所拼的图形画在图4的虚线方框内.
(3)将分解因式:______(直接写出结果,不需要画图).
【答案】(1),或.
(2)方法不唯一,如图:
(3).
【分析】(1) 根据图形分析,正方形、长方形硬纸片8块拼成了一个大长方形的面积,利用面积相等求得等式;
(2)由代数式知这个图形由6块纸片构成,2个小正方形,1个大正方形,3个长方形,拼成一个大长方形,符合题意即可;
(3)依据代数式画出图形,注意式子中有一个减号,所以拼出来的图形是一个长方形,减去了一部分,然后根据图形可以分解因式.
【详解】如图,图中有1个小正方形,3个大正方形,4个长方形构成一个大长方形;
即1个面积为的小正方形,3个面积为大正方形,4个面积为的长方形的面积和,
等于长、宽分别为、的长方形面积.
所以:可以得到等式,
或.
如图:代数式可以看作由2个小正方形,1个大正方形,3个长方形拼成的图形;
依题意画出图形,具体方法可以先把正方形摆好,留下的部分再用长方形填充.
(3) 如图:代数式
可以看作由2个大正方形减去3个长方形的;
此时多减去了1个小正方形再加上1个小正方形.
【点睛】本题考查了代数式的运算,几何图形面积的意义,通过图形拼凑来解;正确的拼图形,采用数形结合理解几何图形面积的意义是解题关键.
14.把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式 ;
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长为a、b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF,若这两个正方形的边长a、b如图标注,且满足a+b=10,ab=20.请求出阴影部分的面积.
(4)图4中给出了边长分别为a、b的小正方形纸片和两边长分别为a、b的长方形纸片,现有足量的这三种纸片.
①请在下面的方框中用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,并仿照图1、图2画出拼法并标注a、b;
②研究①拼图发现,可以分解因式2a2+5ab+2b2= .
【答案】(1);(2)45;(3)20;(4)①见解析,②.
【分析】(1)根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积;另一种是直接利用正方形的面积公式计算,由此即可得出答案;
(2)利用(1)中的等式直接代入即可求得答案;
(3)根据阴影部分的面积等于两个正方形的面积之和减去两个直角三角形的面积即可得;
(4)①依照前面的拼图方法,画出图形即可;
②参照题(1)的方法,根据面积的不同求解方法即可得出答案.
【详解】(1)由题意得:
故答案为:;
(2)
∴
;
(3)四边形ABCD、四边形ECGF为正方形,且边长分别为a、b
,,,
∵
∴
;
(4)①根据题意,作出图形如下:
②根据面积的不同求解方法得:
故答案为:.
【点睛】本题考查了因式分解的几何应用、完全平方公式的几何应用,掌握因式分解的相关知识是解题关键.
15.一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式,比如图②可以解释为:
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示 块, 块, 块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个小长方形的两边长(x>y),观察图案,以下关系式正确的是 (填序号).
①,②,③,④
【答案】(1) (2)2,7,3 (3)①②③④
【分析】(1)根据正方形和矩形的面积公式求解即可.
(2)将展开化简即可得出答案.
(3)逐项按照平方差公式及图形验证即可.
【详解】(1)图③可得,长为,宽为的矩形的面积等于2个边长为的正方形的面积加2个边长为的正方形的面积加5个长为,宽为的矩形的面积
故.
(2)
故答案为:2,7,3.
(3)∵
∴,故①正确
∵
∴②正确
∵
∴,即,故③正确
∵
∴④正确
故答案为:①②③④.
【点睛】本题考查了图形与整式的问题,掌握图形的规律、平方差公式、矩形和正方形的面积公式是解题的关键.
16.一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;
①若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)
②若AB为任意值,且①中的S的值为定值,求a与b的关系.
【答案】(1)(2a+b)(2b+a)=2a2+5ab+2b2;(2)(a﹣b)2,(a﹣b)2=(a+b)2﹣4ab;(3)①S=4ab﹣4b+12a﹣b2;②3a=b.
【分析】(1)根据图形面积可知(2a+b)(2b+a)=2a2+5ab+2b2;
(2)根据阴影部分面积可以是大正方形面积减去四个长方形面积,
得到(a-b)2=(a+b)2-4ab;
(3)①大长方形的面积=(3a+b)(4+b)=7ab+4×3a+4×3a-S;
②设AB=m,大长方形的面积=(3a+b)(m+b)=7ab+3ma+3ma-S,3a-b=0;
【详解】解:(1)根据图可知长方形面积有(2a+b)(2b+a)=2a2+5ab+2b2;
故答案为(2a+b)(2b+a)=2a2+5ab+2b2;
(2)④图中阴影部分面积是(a﹣b)2,
根据阴影部分面积可以是大正方形面积减去四个长方形面积,
∴(a﹣b)2=(a+b)2﹣4ab,
故答案为(a﹣b)2,(a﹣b)2=(a+b)2﹣4ab;
(3)①∵AB=4,长方形AGMB的面积与长方形EDHN的面积的差为S,
∴大长方形的面积=(3a+b)(4+b)=7ab+4×3a+4×3a﹣S,
∴S=4ab﹣4b+12a﹣b2;
②设AB=m,
∴大长方形的面积=(3a+b)(m+b)=7ab+3ma+3ma﹣S,
∴S=4ab﹣b2+m(3a﹣b),
∵若AB为任意值,且①中的S的值为定值,
∴3a=b.
【点睛】本题考查整式的混合运算,熟练掌握多项式乘以多项式的运算法则是解题的关键.
17.我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
(1)根据如图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用如图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(4)两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如图4.请你根据如图中图形的关系,写出一个代数恒等式,并写出推导过程.
【答案】(1);(2)30;(3)9;(4)
【分析】(1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;
(2)根据(1)中结果,求出所求式子的值即可;
(3)根据已知等式,做出相应图形,即可得到结论;
(4)分别表示出各个图形的面积,根据面积关系,即可得出结论.
【详解】解:(1)根据面积关系可得:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=10,ab+bc+ac=35,∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=100﹣70=30;
(3)根据题意得:(2a+b)(a+2b)=,∴x=2,y=5,z=2,∴x+y+z=9;
(4),理由:因为三个图形拼成一个梯形,所以 即.
【点睛】本题主要考查的是整式的混合运算,利用直接法和间接法分别求得几何图形的面积,然后根据它们的面积相等关系列出等式是解题的关键.
18.当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如:由图①,可得等式(a+2b)(a+b)=a2+3ab+2b2.
(1)由图②,可得等式_________________________________________________;
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图③中的纸片(足够多)画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)小明用2张边长为a的正方形、3张边长为b的正方形、5张邻边长分别为a,b的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为____________.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)45;(3)答案见解析;(4) 2a+3b.
【分析】(1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;
(2)根据(1)中的等式,进行变形,求出所求式子的值即可;
(3)根据已知等式,做出长为2a+b,宽为a+2b的长方形图形即可;
(4)根据题意知图形的面积是2a2+5ab+3b2,列出关系式2a2+5ab+3b2=(2a+3b)(a+b),即可确定出长方形较长的边.
【详解】解:(1)由图②可知:正方形的边长为a+b+c,各部分面积分别是:a2,b2,c2,2ab,2ac,2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
故答案是:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=112-2×38=45.
(3)如图所示.
(4)根据题意得:2a2+5ab+3b2=(2a+3b)(a+b),
则较长的一边为2a+3b.
故答案是:2a+3b.
【点睛】本题考查了多项式乘以多项式,弄懂图形的面积的不同表示方法,熟练掌握运算法则是解本题的关键;
19.我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请回答下列问题:
(1)写出图2中所表示的数学等式:_____________.
(2)利用(1)中所得的结论,解决下列问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个长为b、宽为a的长方形纸片.
①请按要求利用所给的纸片拼出一个几何图形,并画在所给的方框内,要求所拼的几何图形的面积为2a2+5ab+2b2;
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式,即2a2+5ab+2b2=________.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)a2+b2+c2=45;
(3)①画图见解析;②(2a+b)(a+2b).
【分析】(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式;
(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出;
(3)①找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件;②根据所给的规律分解因式即可.
(1)
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
故答案为(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)
a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,
=112﹣2×38
=45;
(3)
①如图所示,
②如上图所示的矩形面积=(2a+b)(a+2b),
它是由2个边长为a的正方形、5个边长分别为a、b的长方形、2个边长为b的小正方形组成,所以面积为2a2+5ab+2b2,则2a2+5ab+2b2=(2a+b)(a+2b),
故答案为:(2a+b)(a+2b).
【点睛】本题考查了完全平方公式的几何背景和因式分解的应用,关键是能够把代数式转化成几何图形,用到的知识点是长方形和正方形的面积公式,要认真总结规律,进行答题.
相关试卷
这是一份中考数学专项训练(18)专题圆中不规则图形面积含解析答案,共32页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份考点18 几何图形认识初步(精练),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份七年级数学下册考点精练专题23 平方差公式与几何图形,共29页。









