初中数学中考复习专题10 圆的综合运用（原卷版）

展开

这是一份初中数学中考复习专题10 圆的综合运用（原卷版），共14页。试卷主要包含了选择题，填空题等内容，欢迎下载使用。

专题10 圆的综合运用

一选择题

（南通市崇川区启秀中学一模）一个圆锥的侧面展开图形是半径为8cm，圆心角为的扇形，则此圆锥的底面半径为

A. B. C. 3cm D.

2.(无锡市四校联考一模)如图，AB是的直径，DB、DE别切于点B、C，若，则的度数是

A. B. C. D.

3.(绍兴市一模)如图，AB为⊙O的切线，切点为A．连结AO，BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连结AD．若∠ABC＝36°，则∠ADC的度数为（　　）

A．27° B．32° C．36° D．54°

4.（唐山市遵化市一模）如图，一个边长为4cm的等边三角形ABC的高与的直径相等．与BC相切于点C，与AC相交于点E，则CE的长为

A. 4cm B. 3cm C. 2cm D.

5.（广东省北江实验学校一模）如图， AB是⊙O的直径，且经过弦CD的中点H，

已知cos∠CDB＝，BD＝5，则OH的长度为( )

A. B. C.1 D.

6.(上海市杨浦区一模)如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连接AC，AD，BD，CD，若⊙O的半径是13，BD＝24，则sin∠ACD的值是（　　）

A． B． C． D．

（合肥168中一模）如图，以AD为直径的半圆O经过斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为，则图中阴影部分的面积为

C. D.
8.(无锡市四校联考一模)已知直线与直线同时经过点P，点Q是以为圆心，MO为半径的圆上的一个动点，则线段PQ的最小值为

A. B. C. D.

二填空题

9.(无锡市四校联考一模)圆锥的底面半径为14cm，母线长为21cm，则该圆锥的侧面展开图的圆心角为______度．

10.(绍兴市一模)如图所示，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，若以点C为圆心，r为半径的圆与边AB所在直线有公共点，则r的取值范围为　　．

11.（合肥市天鹅湖教育集团一模）如图，在中，，，，以点A为圆心，以AC为半径画弧，交AB于D，则扇形CAD的周长是_____________（结果保留）．

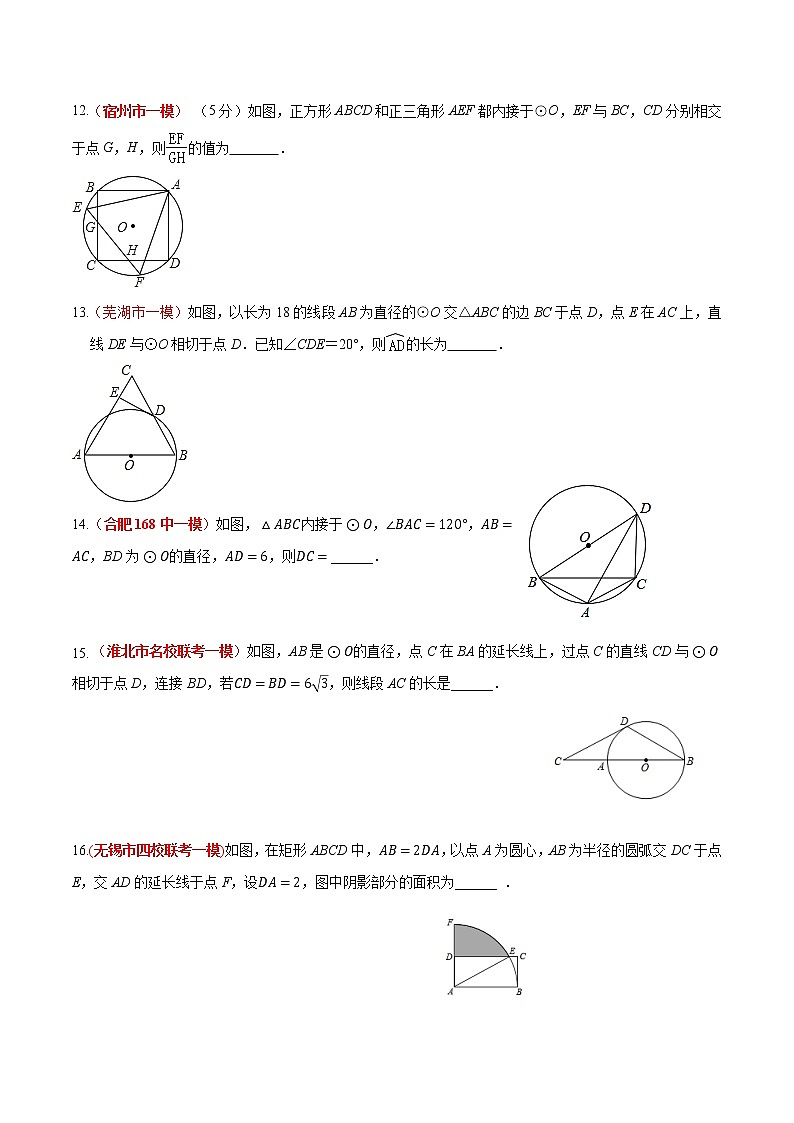
12.（宿州市一模）（5分）如图，正方形ABCD和正三角形AEF都内接于⊙O，EF与BC，CD分别相交于点G，H，则的值为　　．

13.（芜湖市一模）如图，以长为18的线段AB为直径的⊙O交△ABC的边BC于点D，点E在AC上，直线DE与⊙O相切于点D．已知∠CDE＝20°，则的长为　　．

14.（合肥168中一模）如图，内接于，，，BD为的直径，，则______．

（淮北市名校联考一模）如图，AB是的直径，点C在BA的延长线上，过点C的直线CD与相
切于点D，连接BD，若，则线段AC的长是______．

16.(无锡市四校联考一模)如图，在矩形ABCD中，，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设，图中阴影部分的面积为______ ．

三简答题
17.(绍兴市一模)如图，在△ABC中，BA＝BC，以AB为直径的⊙O分别交AC、BC于点D、E，BC的延长线于⊙O的切线AF交于点F．

（1）求证：∠ABC＝2∠CAF；

（2）若AC＝2，CE：EB＝1：4，求CE的长．

18.(沈阳市一模)如图，在Rt△ABC中，∠ACB＝90°，D为AB的中点，以CD为直径的⊙O分别交AC，BC于点E，F两点，过点F作FG⊥AB于点G．

（1）试判断FG与⊙O的位置关系，并说明理由．

（2）若AC＝3，CD＝2.5，求FG的长．

19.（芜湖市一模）已知△ABC是⊙O的内接三角形，∠BAC的平分线交⊙O于点D．

（I）如图①，若BC是⊙O的直径，BC＝4，求BD的长；

（Ⅱ）如图②，若∠ABC的平分线交AD于点E，求证：DE＝DB．

20.（唐山市遵化市一模）如图，在中，，O是边AC上的点，以OC为半径的圆分别交边BC、AC于点D、E，过点D作于点F．
求证：直线DF是的切线；
若，，求劣弧DE的长．

21.（广东省北江实验学校一模）如图，四边形ABCD内接于⊙O，AB=AD，对角线BD为⊙O的直径，AC与BD交于点E．点F为CD延长线上，且DF=BC.

（1）证明：AC=AF；

（2）若AD=2，AF= ，求AE的长；

（3）若EG∥CF交AF于点G，连接DG.证明：DG为⊙O的切线.

22.（宿州市一模）（12分）已知：如图，MN为⊙O的直径，ME是⊙O的弦，MD垂直于过点E的直线DE，垂足为点D，且ME平分∠DMN．

求证：（1）DE是⊙O的切线；

（2）ME2＝MD•MN．

23.（淮北市名校联考一模）如图，在中，，，以AB为直径作，连接OC，过点B作交于点D，连接AD交OC于点E．
求证：；
若的半径为2，求OE的长．

(无锡市四校联考一模)如图，的顶点A，C在上，与AB相交于点D，连接CD，，．
求圆心O到弦DC的距离；
若，求证：BC是的切线．

25.（南通市崇川区启秀中学一模）在平面直角坐标系xOy中，的半径为，P是圆内与圆心C不重合的点，的“完美点”的定义如下：若直线CP与交于点A，B，满足，则称点P为的“完美点”，如图为及其“完美点”P的示意图．
当的半径为2时，
在点，，中，的“完美点”是______；
若的“完美点”P在直线上，求PO的长及点P的坐标；
的圆心在直线上，半径为2，若y轴上存在的“完美点”，求圆心C的纵坐标t的取值范围．

26.(无锡市四校联考一模)如图，矩形ABCD中，，动点E，F同时分别从点A，B出发，分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动，连接EF，以EF为直径作交射线BD于点M，设运动的时间为t．
当点E在线段AD上时，用关于t的代数式表示DE，DM．
在整个运动过程中，
连结CM，当t为何值时，为等腰三角形．
圆心O处在矩形ABCD内包括边界时，求t的取值范围，并直接写出在此范围内圆心运动的路径长．