初中数学中考复习 专题15 动点综合问题（原卷版）

这是一份初中数学中考复习 专题15 动点综合问题（原卷版），共23页。

【考点1】动点之全等三角形问题
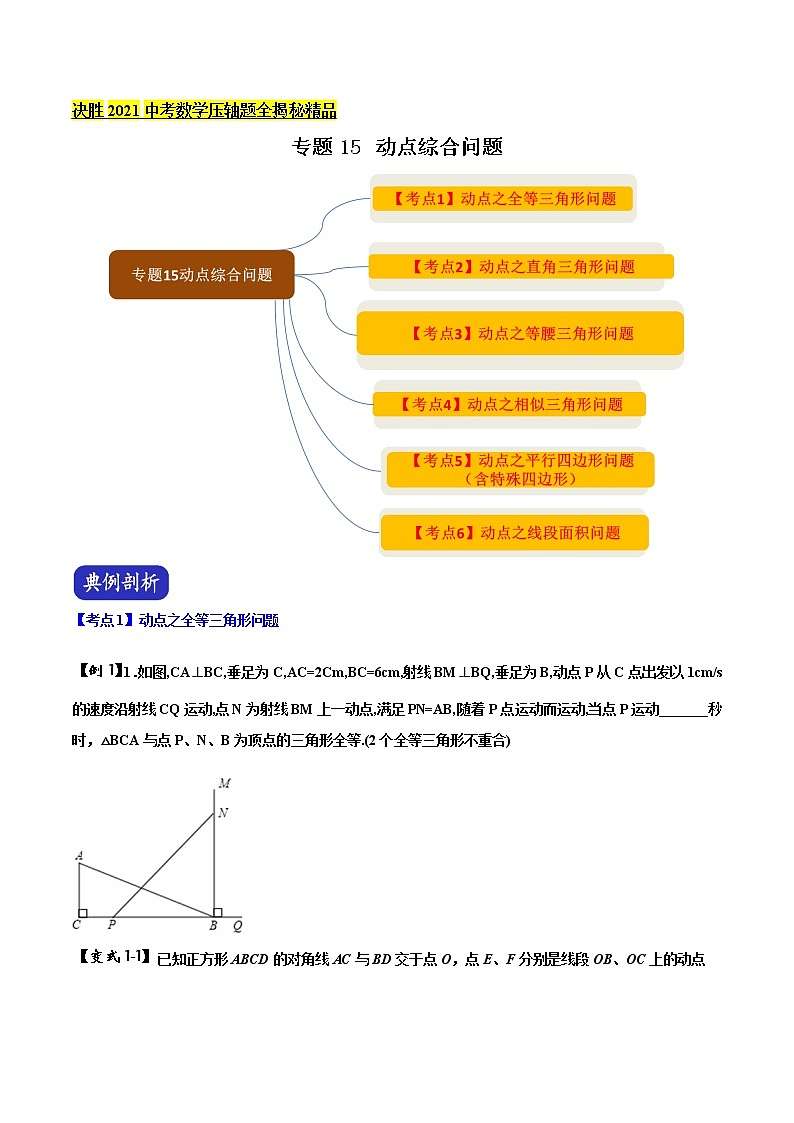
【例1】1．如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时，△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)
【变式1-1】已知正方形ABCD的对角线AC与BD交于点O，点E、F分别是线段OB、OC上的动点
（1）如果动点E、F满足BE＝OF（如图），且AE⊥BF时，问点E在什么位置？并证明你的结论；
（2）如果动点E、F满足BE＝CF（如图），写出所有以点E或F为顶点的全等三角形（不得添加辅助线）．
【变式1-2】如图①，将长方形纸片沿对角线剪成两个全等的直角三角形ABC、EDF，其中AB＝8cm，BC＝6cm，AC＝10cm．现将△ABC和△EDF按如图②的方式摆放（点A与点D、点B与点E分别重合）．动点P从点A出发，沿AC以2cm/s的速度向点C匀速移动；同时，动点Q从点E出发，沿射线ED以acm/s （0＜a＜3）的速度匀速移动，连接PQ、CQ、FQ，设移动时间为ts （0≤t≤5）．
（1）当t＝2时，S△AQF＝3S△BQC，则a＝ ；
（2）当以P、C、Q为顶点的三角形与△BQC全等时，求a的值；
（3）如图③，在动点P、Q出发的同时，△ABC也以3cm/s的速度沿射线ED匀速移动，当以A、P、Q为顶点的三角形与△EFQ全等时，求a与t的值．
【考点2】动点之直角三角形问题
【例2】如图，在四边形纸片中，，，，，，点是边上的动点，点是折线上的动点，将纸片沿直线折叠，使点的对应点落在边上，连接，若是直角三角形，则的长为________．
【变式2-1】（2019·辽宁中考模拟）如图，已知二次函数y＝ax2+bx+4的图象与x轴交于点A(4，0)和点D(﹣1，0)，与y轴交于点C，过点C作BC平行于x轴交抛物线于点B，连接AC
(1)求这个二次函数的表达式；
(2)点M从点O出发以每秒2个单位长度的速度向点A运动；点N从点B同时出发，以每秒1个单位长度的速度向点C运动，其中一个动点到达终点时，另一个动点也随之停动，过点N作NQ垂直于BC交AC于点Q，连结MQ.
①求△AQM的面积S与运动时间t之间的函数关系式，写出自变量的取值范围；当t为何值时，S有最大值，并求出S的最大值；
②是否存在点M，使得△AQM为直角三角形？若存在，求出点M的坐标；若不存在，说明理由．
【变式2-2】如图，在矩形中， ，为中点，连接. 动点从点出发沿边向点运动，动点从点出发沿边向点运动，两个动点同时出发，速度都是每秒1个单位长度，连接，设运动时间为（秒）. 则_____时，为直角三角形
【考点3】动点之等腰三角形问题
【例3】如图，是⊙的直径，是弦，，．若点是直径上一动点，当 是等腰三角形时，__________．
【变式3-1】如图①，已知正方形边长为2，点是边上的一个动点，点关于直线的对称点是点，连结、、、.设AP=x.
（1）当时，求长；
（2）如图②，若的延长线交边于，并且，求证：为等腰三角形；
（3）若点是射线上的一个动点，则当为等腰三角形时，求的值.
【变式3-2】（2019·河南中考模拟）如图，抛物线y=ax2+bx+3交y轴于点A，交x轴于点B（-3，0）和点C（1，0），顶点为点M．
（1）求抛物线的解析式；
（2）如图，点E为x轴上一动点，若△AME的周长最小，请求出点E的坐标；
（3）点F为直线AB上一个动点，点P为抛物线上一个动点，若△BFP为等腰直角三角形，请直接写出点P的坐标．
【变式3-3】（2019·广西中考真题）已知抛物线和直线都经过点，点为坐标原点，点为抛物线上的动点，直线与轴、轴分别交于两点．
（1）求的值；
（2）当是以为底边的等腰三角形时，求点的坐标；
（3）满足（2）的条件时，求的值．
【考点4】动点之相似三角形问题
【例4】如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，求AP的长．
【变式4-1】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝AC
（1）求过点A，B的直线的函数表达式；
（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．
【变式4-2】如图，正方形ABCD，点P为射线DC上的一个动点，点Q为AB的中点，连接PQ，DQ，过点P作PE⊥DQ于点E．
（1）请找出图中一对相似三角形，并证明；
（2）若AB＝4，以点P，E，Q为顶点的三角形与△ADQ相似，试求出DP的长．
【考点5】动点之平行四边形问题（含特殊四边形）
【例5】如图，抛物线与轴交于两点，与轴交于点．
（1）求抛物线的解析式；
（2）点是抛物线上的动点，且满足，求出点的坐标；
（3）连接，点是轴一动点，点是抛物线上一动点，若以、、、为顶点的四边形是平行四边形时，请直接写出点的坐标．
备用图
【变式5-1】（2019·江西中考真题）在图1，2，3中，已知，，点为线段上的动点，连接，以为边向上作菱形，且．
（1）如图1，当点与点重合时，________°；
（2）如图2，连接．
①填空：_________（填“>”，“