人教版数学七下 第六章 章末复习 课件+教案+导学案

本章复习

【知识与技能】

掌握本章基本概念与运算,能用本章知识解决实际问题.

【过程与方法】

通过梳理本章知识点,挖掘知识点间的联系,并应用于实际解题中.

【情感态度】

领悟分类讨论思想,学会类比学习的方法.

【教学重点】

本章知识梳理及掌握基本知识点.

【教学难点】

应用本章知识解决实际与综合问题.

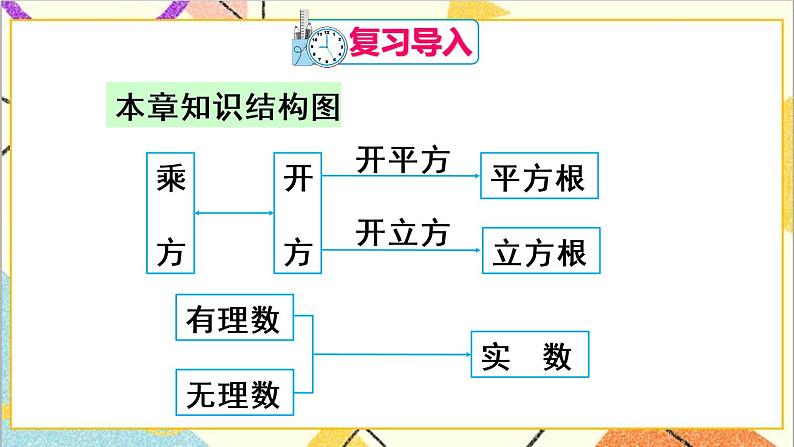
一、知识框图，整体把握

【教学说明】1.通过构建框图,帮助学生回忆本节所有基本概念和基本方法.

2.帮助学生找出知识间联系,如平方与开平方,平方根与立方根,有理数与实数等等.

二、释疑解惑，加深理解

1.利用平方根的概念解题

在利用平方根的概念解题时,主要涉及平方根的性质:正数有两个平方根,且它们互为相反数;以及平方根的非负性:被开方数为非负数,算术平方根也为非负数.

例1已知某数的平方根是a+3及2a-12,求这个数.

分析：由题意可知,a+3与2a-12互为相反数,则它们的和为0.

解:根据题意可得,a+3+2a-12=0.

解得a=3.

∴a+3=6,2a-12=-6.

∴这个数是36.

【教学说明】负数没有平方根,非负数才有平方根,它们互为相反数,而0是其中的一个特例.

2.比较实数的大小

除常用的法则比较实数大小外,有时要根据题目特点选择特别方法.

例2比较与的大小.

分析：先比较它们的绝对值与的大小，然后由绝对值大的反而小得出结论.可用平方法比较,即分别将与平方,平方数大的实数大.

【教学说明】用平方法比较实数的大小,是运用下列推理:当a＞0,b＞0时,若a2＞b2,则a＞b;若a＞b＞0,则.

3.实数的运算

实数的有关运算律及运算顺序、相反数、绝对值等与有理数的运算基本相同.有理数的运算律及运算顺序对实数同样适用.

【教学说明】在进行实数混合运算时,首先要观察算式的特点,选择合适的方法进行计算.一般按照先乘方,后乘除,再加减的顺序计算,另外还要注意符号.

三、典例精析，复习新知

例1 如图所示,数轴上表示的点是          .

分析：由于1＜3＜4,故1＜3＜2,故这样的点在表示1和2的点之间,故选C.

【教学说明】本题是用估算法确定结果,其方法是找到与被开方数最接近的两个平方数来界定范围.

例2已知a,b是实数,且+|b-|=0,解关于x的方程(a+2)x+b2=a-1.

分析：先利用非负数的性质求出a,b的值,再解方程.

【教学说明】本题由两个非负数的和为0,得到两个非负数为0,求出a,b的值,再代入方程求解.

【教学说明】本题是应用定义求解的,这启示我们,数学定义是解数学题最基本的依据.

例4已知a是的整数部分,b是的小数部分,求2a+b的值.

解：因为16＜19＜25,所以＜＜,即4＜＜5,从而a=4,

b=-4,2a+b=8+-4=4+.

【教学说明】一个数x是整数部分与小数部分的和,由特例可归纳求一个数整数部分与小数部分的方法,如数为4.1,则整数部分为4,而小数部分0.1=4.1-4,即小数部分=数x-x的整数部分.

例5对于正数x,y,有下列命题:

若x+y=2,则≤1;若x+y=3,则xy≤3/2;若x+y=6,则≤3.根据以上三个命题所提供的规律猜想:

(1)若x+y=9,则≤      .

(2)若对于任意正数a,b,总有≤      .

(3)由此能得到什么结论?

【教学说明】用探究型活动问题指导学生互相讨论,给出足够的时间供学生思考,教师予以点拨.

1.布置作业：从课本“复习题6”中选取.

2.完成练习册中本课时的练习.

1.本课时教学可应用不同形式的练习引导学生认识相关的基本概念，强化对基本概念的理解以利于进行运算与判断.

2.注重分类思想的认识与理解，强调实数计算能力的训练，打下坚实的运算能力的基础.