





人教版数学四下 第五单元 第3课时 三角形三边的关系 课件+教案+导学案
展开第2课时 两点间的距离及三角形三边的关系
课题 | 两点间的距离及三角形三边的关系 | 课型 | 新授课 | ||
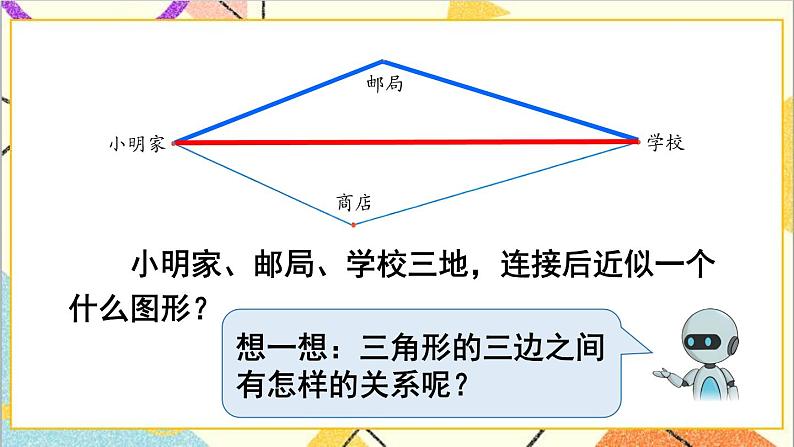
设计说明 | 本节课的教学内容是让学生理解三角形三条边的关系——任意两边的和大于第三边。根据本节课教学内容的特点,我做了如下的教学设计: 1.创设情境,调动学生的学习兴趣。 在新课开始时,我就设计一个和实际生活联系紧密的情境:小明去学校该如何选择路线?由此引起学生猜想、回答的欲望。利用3根小棒摆三角形的实验,把全体学生充分地调动起来,亲自动手,亲自实践。这些动手操作、共同探究的活动,既满足了学生动手操作的需要,又让学生在高昂的学习兴趣中学到了知识,体验到了学习的乐趣。 2.联系已有的生活经验,发现新知。 本节课通过让学生仔细观察小明上学的路线图,发现连接小明家、商店、学校三地的路线是一个近似三角形,而连接小明家、邮局、学校三地的路线同样也是近似三角形。走中间这条路实际上就是走三角形的一条边,走“小明家——商店——学校”或走“小明家——邮局——学校”的路线实际上就是走三角形的另外两条边,走三角形的两条边的路程和要比走第三边的路程远,这就引出了这节课要探究的问题:是不是所有三角形的3条边都有这样的关系呢?在探究这个问题时,让每个小组用小棒来摆三角形,通过实际操作、探究,得出:三角形任意两边的和大于第三边,这样不仅把枯燥的数学学习与学生的生活实际相联系,还使学生感受到数学就在我们身边,并体会到学习数学的乐趣。 | ||||
学习目标 | 1.探究三角形边的关系,知道三角形任意两边之和大于第三边。 2.根据三角形的关系,解释生活中的一些实际问题、现象,培养运用数学知识解决问题的能力。 3.培养学生的动手操作能力。 | ||||
学习重点 | 理解并掌握三角形三边的关系。 | ||||
学习难点 | 应用三角形边的关系解决问题。 | ||||
学前准备 | 教具准备:多媒体课件、长度不同的小棒 学具准备:长度不同的小棒 | ||||
课时安排 | 1课时 | ||||
教学环节 | 导案 | 学案 | 达标检测 | ||
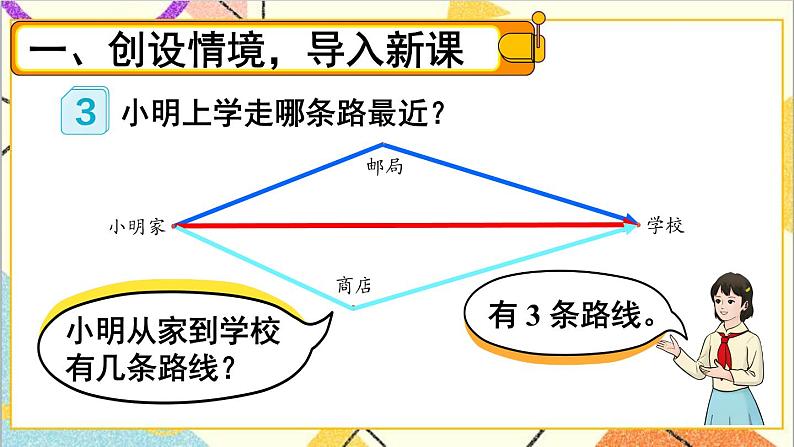
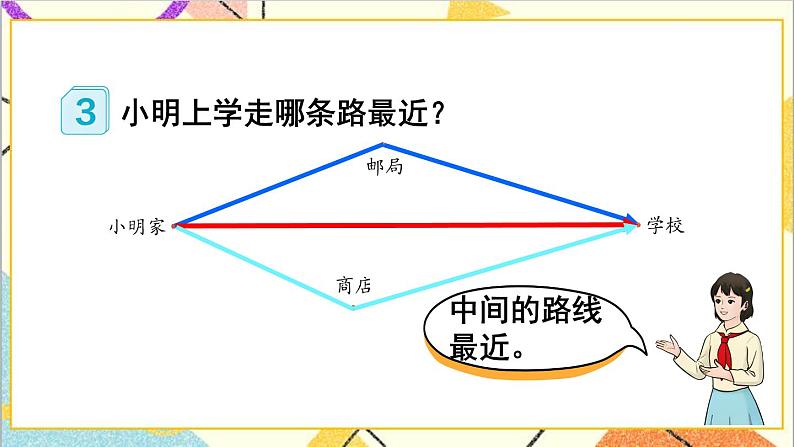
一、创设情境,提出问题。(7分钟) | 1.课件出示例3小明家到学校的路线图,组织学生讨论: 从小明家到学校有几条路?哪条路最近?并说明理由。 2.设疑引入:这是什么原因呢?这个问题可以用三角形三边之间的关系来解释,下面我们就来探讨三角形三边的关系。 | 1.看图交流,汇报并说明理由。两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。 2.明确本节课学习内容。 | 1.数一数下面图形中有几个三角形。 ( )个 答案:6 2.能围成三角形的各组线段的后面画“√”(单位:cm)。 (1)456( ) (2)6410( ) (3)342( ) (4)4814( ) 答案:√×√× 3.每组中的三根小棒能围成三角形吗? 答案:第①、④组能围成。 | ||
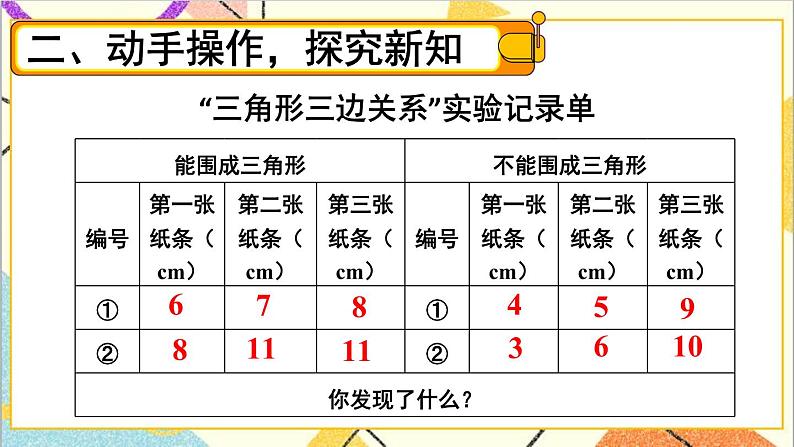
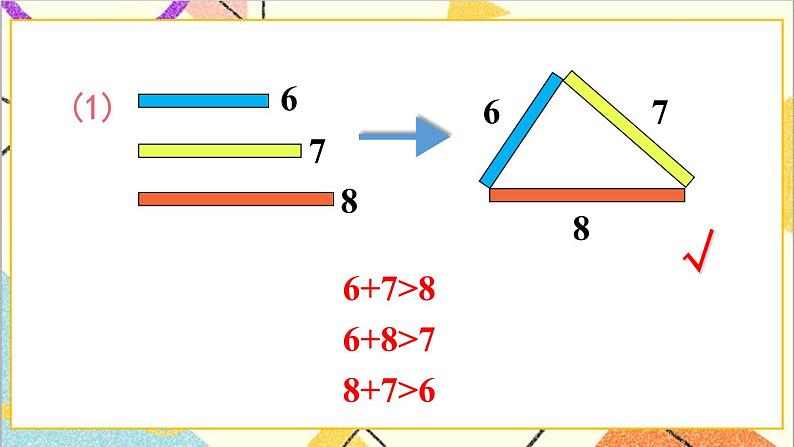
二、操作验证,探究新知。(18分钟) | 1.组织学生用下面每组小棒摆一摆,看哪组能摆成三角形。(单位:cm) (1)6、7、8。 (2)4、5、9。 (3)3、6、10。 (4)8、11、11。 2.讨论:为什么第(2)组和第(3)组小棒不能摆成三角形? 3.计算验证,得出结论。 4.引导学生用这一结论说明例3中的问题。 | 1.用每组的小棒摆三角形。 2.用每组小棒比一比,发现:其中(2)(3)组有两根小棒的长度之和小于或等于第三根小棒的长度。 3.计算验证得出: (1)6+7>8能摆成三角形。 (2)4+5=9不能摆成三角形。 (3)3+6<10不能摆成三角形。 (4)8+11>11能摆成三角形。 结论:三角形任意两边的和大于第三边。 4.讨论并说明例3中的问题。 | |||
三、巩固练习,应用反馈。 (12分钟) | 1.下面线段中哪三条线段能围成三角形? 6cm 8cm 5cm 4cm 2.三角形三条边都是整厘米数,其中两条边分别长4厘米、6厘米,第三条最长是几厘米?最短是几厘米? | 1.独立找出答案,小组内交流,互相补充再汇报,并说明理由。 2.先独立完成,再汇报。 | 教学过程中老师的疑问: | ||
四、课堂总结。(3分钟) | 1.总结本节课的学习内容。 2.布置课后学习内容。 | 谈自己本节课的收获。 | |||
五、教学板书 | |||||
六、教学反思 | 本节课,学生大多处于探究活动中,学生的探究活动是在学生的自主探究前提下进行的,用长度一定的三根小棒任意摆三角形的设计具有开放性,没有规定摆弄的顺序,使学生的探究不受局限。观察和推理时,完全由学生运用自己的语言解释现象,形象、生动、易懂。 在探究认识三角形的三边的关系时,先让学生动手操作,再引导学生讨论不能围成三角形的小棒长度的变化。让学生体会到了三角形任意两边的和大于第三边这一规律的含义,尤其是对“任意”两字的进一步体会和理解。 | ||||
教师点评和总结:
| |||||











