初中数学湘教版七年级下册1.1 建立二元一次方程组教案

这是一份初中数学湘教版七年级下册1.1 建立二元一次方程组教案，共7页。教案主要包含了课前预习，例题欣赏，课堂练习，课后练习，课后提高练习等内容，欢迎下载使用。
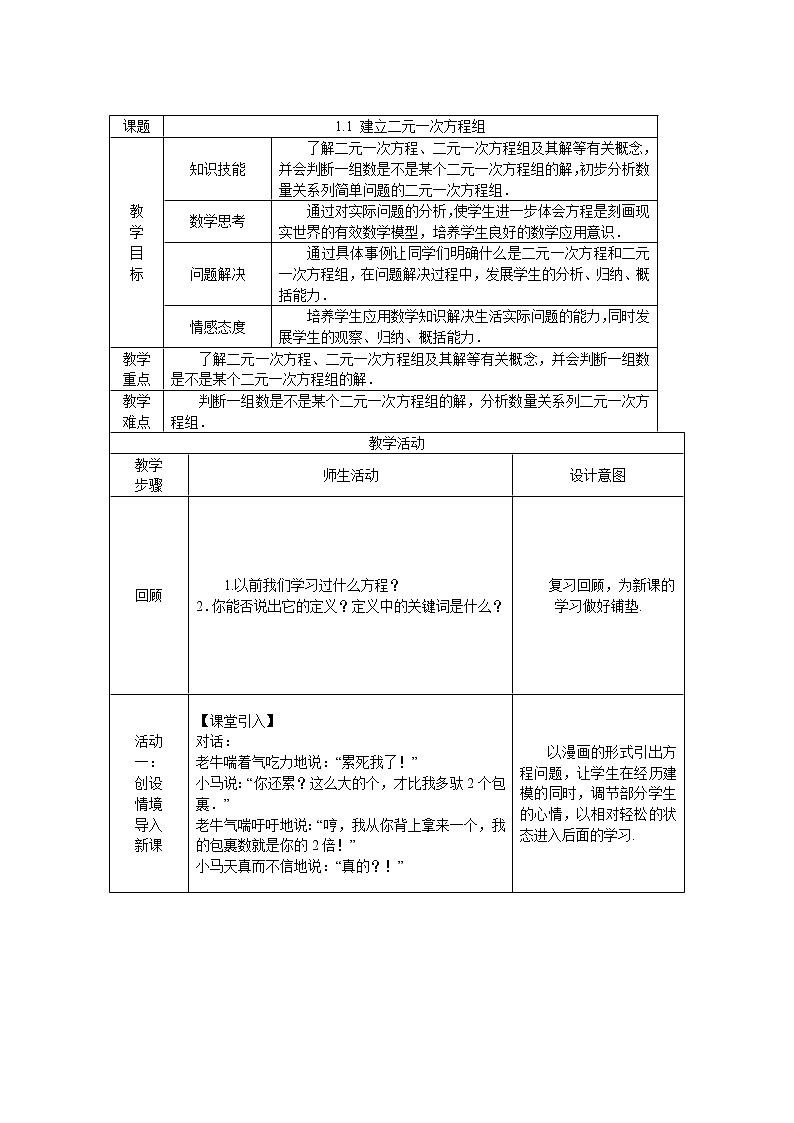
 课题1.1 建立二元一次方程组教学目标知识技能　　了解二元一次方程、二元一次方程组及其解等有关概念，并会判断一组数是不是某个二元一次方程组的解，初步分析数量关系列简单问题的二元一次方程组．数学思考　　通过对实际问题的分析，使学生进一步体会方程是刻画现实世界的有效数学模型，培养学生良好的数学应用意识．问题解决　　通过具体事例让同学们明确什么是二元一次方程和二元一次方程组，在问题解决过程中，发展学生的分析、归纳、概括能力．情感态度　　培养学生应用数学知识解决生活实际问题的能力，同时发展学生的观察、归纳、概括能力．教学重点　　了解二元一次方程、二元一次方程组及其解等有关概念，并会判断一组数是不是某个二元一次方程组的解．教学难点　　判断一组数是不是某个二元一次方程组的解，分析数量关系列二元一次方程组．教学活动教学步骤师生活动设计意图回顾　　1.以前我们学习过什么方程？2．你能否说出它的定义？定义中的关键词是什么？　　复习回顾，为新课的学习做好铺垫.活动一：创设情境导入新课【课堂引入】对话：老牛喘着气吃力地说：“累死我了！”小马说：“你还累？这么大的个，才比我多驮2个包裹．”老牛气喘吁吁地说：“哼，我从你背上拿来一个，我的包裹数就是你的2倍！”小马天真而不信地说：“真的？！”图3问题1：从它们的对话中，你最想知道什么？问题2：如果假设老牛驮了x个包裹，小马驮了y个包裹，你能得到怎样的方程？能列几个？以漫画的形式引出方程问题，让学生在经历建模的同时，调节部分学生的心情，以相对轻松的状态进入后面的学习.活动二：实践探究交流新知【探究1】 二元一次方程的概念观察并思考：x－y＝2；x＋1＝2(y－1)；x＋y＝8；5x＋3y＝34.(1)观察以上几个方程，它们各含有几个未知数？含未知数的项的次数是多少？与一元一次方程有何异同？(2)能否仿照一元一次方程的定义给这几个方程起个名？归纳总结：含有两个未知数(二元)，并且含未知数的项的次数都是1的整式方程叫二元一次方程．它有三个特征：(1)含有两个未知数；(2)所含未知数的项的次数都是1；(3)方程的两边都是整式．巩固练习一：下列方程中，哪些是二元一次方程：________．(1)x＋3y－9＝0；(2)3x2－2y＋12＝0；(3)3a－4b＝7；(4)3x－＝1；(5)3x(x－2y)＝5；(6)－5n＝1.【探究2】 二元一次方程组的概念对于活动一中的问题可以列出x－y＝2和x＋1＝2(y－1)这两个方程，其中x的含义是什么？y的含义是什么？两个方程中x，y的含义一样吗？总结：两个方程中x，y的含义是一样的．说明：x，y同时满足两个方程，所以我们把它们联立起来，在前面加一个大括号，组成方程组像这样，把两个含有相同未知数的二元一次方程(或者一个二元一次方程，一个一元一次方程)联立起来，组成的方程组，叫做二元一次方程组．巩固练习二：判断下列方程组是不是二元一次方程组：(1)(2)(3)(4)(5)(6)【探究3】 二元一次方程(组)的解做一做：(1)x＝6，y＝2适合方程x＋y＝8吗？x＝5，y＝3呢？x＝4，y＝4呢？你还能找到其他x，y的值适合方程x＋y＝8吗？(2)x＝5，y＝3适合方程5x＋3y＝34吗？x＝2，y＝8呢？(3)你能找到一组x，y，同时适合方程x＋y＝8和5x＋3y＝34吗？x＝5，y＝3是二元一次方程x＋y＝8的一个解，记作同样也是二元一次方程5x＋3y＝34的一个解．同时适合x＋y＝8和5x＋3y＝34，那么，我们就说是二元一次方程组的解．归纳总结：在一个二元一次方程组中，使每一个方程的左、右两边的值都相等的一组未知数的值，叫做这个方程组的一个解．巩固练习三：1.下列四组数值中，哪些是二元一次方程x－3y＝1的解？(1)(2)(3)(4)2．二元一次方程组的解是(　　)A.  B.  C.  D. 　　让学生利用类比的方法，归纳、概括出二元一次方程的概念，抓住概念的关键特征．          使学生理解未知数x和y表示的意义相同，规范方程组的表示方法.                     对比一元一次方程解的概念，让学生归纳、概括二元一次方程(组)解的概念，提高学生的语言组织能力，深刻理解方程组的解的概念，通过练习强化概念.        活动三：开放训练体现应用  【应用举例】例1　如果方程2xm－1－3y2m＋n＝1是二元一次方程，那么m＝________，n＝________．例2　请写出一个二元一次方程组____________，使它的解是例3　以为解的二元一次方程组是(　　)A.  B.C.  D.例4　关于x，y的方程组的解是则|m－n|的值是(　　)A．5  B．3  C．2  D．1学生通过例题巩固刚刚学习的新知识，在此基础上加深知识的应用.【拓展提升】例5　已知关于x，y的方程(2m－6)x|n|＋1＋(n＋2)ym2－8＝0是二元一次方程，求m，n的值．例6　已知是方程组的解，则a＋b的值为多少？学生自主探索，巩固知识，提高技能，从而提高综合运用知识的能力.活动四：课堂总结反思【当堂训练】1.下列方程组中，属于二元一次方程组的是(　　)A.  B.C.  D.2.二元一次方程x－2y＝1有无数个解，下列四组值中不是该方程的解的是(　　)A.  B.  C.  D.3．方程组的解是(　　)A.  B.  C.  D.4．根据题意列方程组：小明从邮局买了面值50分和80分的邮票共9枚，花了6.3元，小明买了两种邮票各多少枚？巩固所学知识，了解学生对本课所学知识的掌握情况，发现不足，查漏补缺，从而达到巩固提高的目的.【课堂总结】布置作业：1．教材P4练习T1，T2，T3.2．教材P5习题1.1A组T1，T2，T3.　　布置作业，专题突破. 　　框架图式总结，更容易形成知识网络.活动四：课堂总结反思　　　　　【教学反思】①[授课流程反思]通过创设情境，让学生感受数学知识的产生、发展与形成过程，通过自主探究、合作交流的教学方式，培养学生观察、比较、分析、思考、探究的能力，在教学过程中，不但注重数学知识的产生与形成过程，同时注重思想方法与情感教育的渗透，使学生的思想情感得到升华．②[讲授效果反思]用老牛和小马之间的对话引出课题，培养学生学习数学的兴趣，并结合知识网络说明本节课要掌握的内容，使学生完成从一元到二元的认识转化过程，体现了方程的建模思想．③[师生互动反思]主要运用了类比的思想方法，通过与一元一次方程的比较引出二元一次方程的概念，有助于学生对新知识的理解．④[习题反思]好题题号___________________________________错题题号___________________________________　反思，更进一步提升. 二元一次方程组学案一、课前预习什么叫二元一次方程？什么叫二元一次方程组？   什么叫二元一次方程的解？什么叫二元一次方程组的解？如何检验方程组的解？    二、例题欣赏例1.已知，在下列四组数值中哪些是方程（1）的解？哪些是方程（2）的解？哪些是方程组的解？①；②；③；④。 例2.某班共有学生49人，一天该班某男生因事请假，当天的男生人数恰好为女生人数的一半，若设该班男生人数为，女生人数为，则可列出方程组为（   ）A)      B)     C)     D) 三、课堂练习1.以为解的二元一次方程组为（   ）A)       B)       C)       D)2.某校七年级学生到礼堂开会，若每条长凳坐5人，则少10条长凳；若每条长凳坐6人，则多余2条长凳；如果设学生人数为，长凳的条数为，则可列方程组为（   ）A)    B)      C)    D 四、课后练习1.在下列四个方程中是二元一次方程的为（   ）A)       B)     C)      D)2.在下列方程组中是二元一次方程组的有（   ）①；②；③；④；⑤；⑥A)6个            B)5个           C)4个            D)3个3.方程组的解为（   ）A)  B)  C)  D)4.某蔬菜公司收购到某种蔬菜140吨，准备加工上市销售，该公司的加工能力是：每天可以精加工6吨或粗加工16吨；现计划用15天完成加工任务，该公司应安排几天精加工，几天粗加工？设安排天精加工，天粗加工，则可列方程组为（   ）A)    B)   C)    D)5.写出满足方程的一组整数值为________________五、课后提高练习6.如图示表示有若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有盆花，每个图案中花盆的总数为，按此规律推断，以为未知数的二元一次方程为__________________7.已知方程是二元一次方程，则_______，______8.已知方程组和具有相同的解，求的值。