第六章　章末整合课件PPT

这是一份第六章　章末整合课件PPT，共35页。

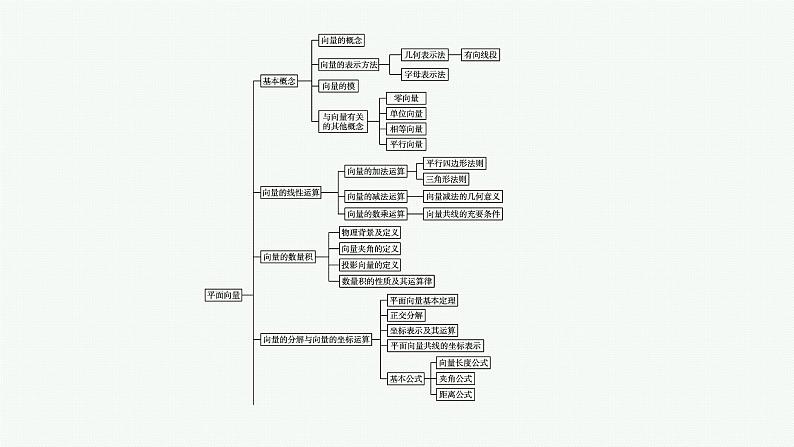
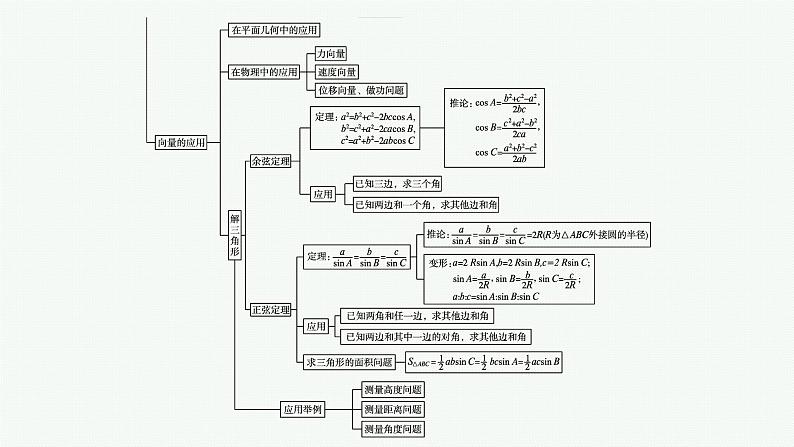
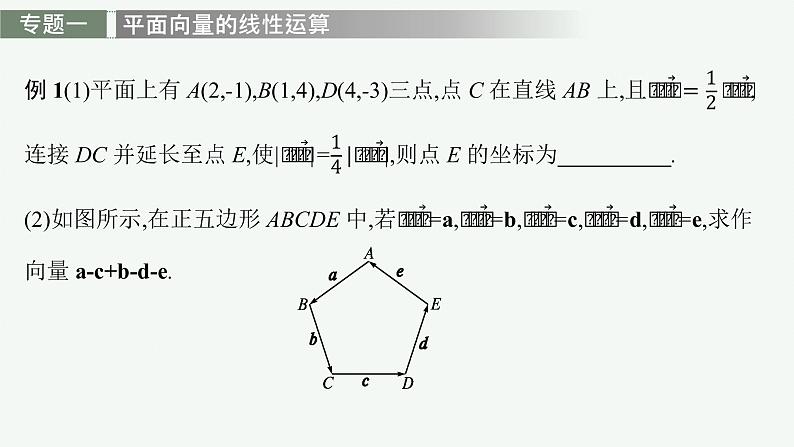
高中同步学案优化设计GAO ZHONG TONG BU XUE AN YOU HUA SHE JI第六章2022内容索引知识网络系统构建题型突破深化提升知识网络系统构建题型突破深化提升名师点析1.向量加法是由三角形法则定义的,要点是“首尾相接”,即 .2.向量减法实质是向量加法的逆运算,是相反向量的作用.3.数乘运算即通过实数与向量的乘积,实现同向或反向上向量长度的伸缩变换.名师点析向量数量积的求解策略(1)利用数量积的定义、运算律求解.在数量积运算律中,有两个形似实数的完全平方公式在解题中的应用较为广泛,即(a+b)2=a2+2a·b+b2,(a-b)2=a2-2a·b+b2,上述两公式以及(a+b)·(a-b)=a2-b2这一类似于实数平方差的公式在解题过程中可以直接应用.(2)借助零向量.即借助“围成一个封闭图形且首尾相接的向量的和为零向量”,再合理地进行向量的移项以及平方等变形,求解数量积.(3)借助平行向量与垂直向量.即借助向量的分解,将待求的数量积转化为有垂直关系或平行关系的向量数量积,借助a⊥b,则a·b=0等解决问题.(4)建立平面直角坐标系,利用坐标运算求解数量积.答案 D 例3(1)(2021全国甲卷)已知向量a=(3,1),b=(1,0),c=a+kb.若a⊥c,则k=　　　　　. (2)设A,B,C,D为平面内的四点,且A(1,3),B(2,-2),C(4,1).解析 ∵a⊥c,∴a·c=0,即a·(a+kb)=0,∴a2+ka·b=0, 所以(2,-2)-(1,3)=(x,y)-(4,1),即(1,-5)=(x-4,y-1).名师点析1.证明向量共线问题常用的方法(1)向量a,b(a≠0)共线⇔存在唯一的实数λ,使b=λa.(2)向量a=(x1,y1),b=(x2,y2)共线⇔x1y2-x2y1=0.(3)向量a与b共线⇔|a·b|=|a||b|.(4)向量a与b共线⇔存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.2.证明平面向量垂直问题的常用方法a⊥b⇔a·b=0⇔x1x2+y1y2=0,其中a=(x1,y1),b=(x2,y2).所以ka-b=(k-3,-5k+2),a+3b=(10,-11).因为ka-b与a+3b垂直,例4在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b+c=2acos B.(1)求证:A=2B;证明 由正弦定理得sin B+sin C=2sin Acos B,故2sin Acos B=sin B+sin(A+B)=sin B+sin Acos B+cos Asin B,于是sin B=sin(A-B).又A,B∈(0,π),故0