高中数学人教A版 (2019)必修 第二册7.1 复数的概念图片课件ppt

这是一份高中数学人教A版 (2019)必修 第二册7.1 复数的概念图片课件ppt，共37页。PPT课件主要包含了内容索引，课前篇自主预习，课堂篇探究学习，激趣诱思，知识点拨，实数0对应零向量，面向量，答案C，答案D，答案AB等内容，欢迎下载使用。
1.了解复平面的概念.(数学抽象)2.理解复数、复平面内的点、复平面内的向量之间的对应关系.(逻辑推理)3.掌握复数模和共轭复数的概念,会求复数的模和共轭复数.(数学运算)
我们知道,实数与数轴上的点一一对应,也就是说,数轴可以看成实数的一个几何模型.那么,能否为复数找一个几何模型呢?怎样建立起复数与几何模型中点的一一对应关系?
知识点一、复数的几何意义1.复平面(1)复平面:建立了直角坐标系来表示复数的平面叫做复平面;(2)实轴:坐标系中的x轴叫做实轴,实轴上的点都表示实数;(3)虚轴:坐标系中的y轴叫做虚轴,除了原点外,虚轴上的点都表示纯虚数.
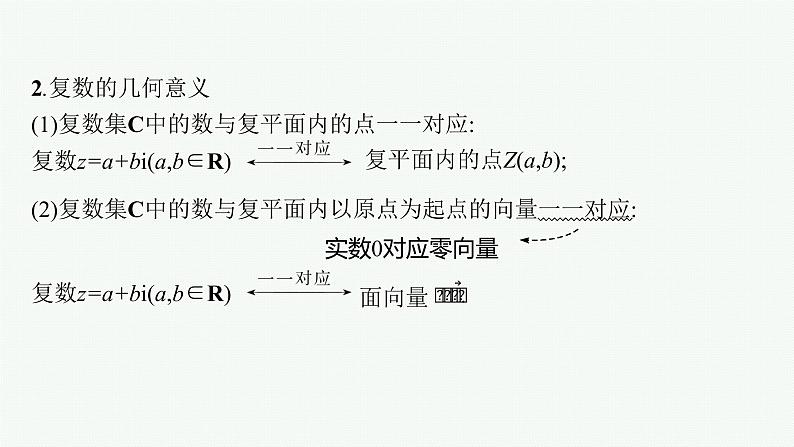
2.复数的几何意义(1)复数集C中的数与复平面内的点一一对应:　
(2)复数集C中的数与复平面内以原点为起点的向量一一对应:
复平面内的点Z(a,b);
复数z=a+bi(a,b∈R)
要点笔记复数与平面向量建立一一对应关系的前提是向量的起点为原点,否则,不能建立一一对应关系.
微练习(1)复数z=3-5i在复平面内对应的点的坐标是(　　)A.(3,-5)　　　　　B.(3,5)C.(3,-5i) D.(3,5i)
A.等于0B.等于-3C.在虚轴上D.既不在实轴上,也不在虚轴上
答案 (1)A　(2)C
解析(1)复数z=3-5i在复平面内对应的点的坐标是(3,-5).(2)向量 对应的复数为-3i,在虚轴上.
知识点二、复数的模1.定义:向量 的模叫做复数z=a+bi(a,b∈R)的模或绝对值,记作|z|或|a+bi|.2.求法:|z|=|a+bi|= ,其中a,b∈R.3.模的几何意义:复数z的模就是复数z=a+bi(a,b∈R)所对应的点Z(a,b)到原点(0,0)的距离.
微练习(1)复数4-2i的模等于(　　)
(2)判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.①复数的模一定是正实数.(　　)②两个复数相等,它们的模一定相等,反之也成立.(　　)
答案 (1)C　(2)①×　②×
知识点三、共轭复数一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数.复数z的共轭复数用 表示,即如果z=a+bi,那么 =a-bi.
要点笔记(1)设z1=a+bi,对应的点为Z1(a,b),Z2=a-bi,对应的点为Z2(a,-b),点Z1与Z2关于实轴对称.(2)若复数z=a+bi(a,b∈R),则z= ⇔b=0.
微练习已知复数z=3+4i,则z的共轭复数的模为　　　　　. 答案 5
例1当复数z= +(a2-2a-15)i(a∈R)在复平面内对应的点Z满足下列条件时,求a的取值范围.(1)点Z在复平面的第二象限内;(2)点Z在复平面内的实轴上方.分析确定z的实部、虚部→列不等式组→解参数取值范围
即(a+3)(a-5)>0,解得a>5或a