





- 第五章相交线的小结与复习课件 课件 0 次下载
- 6.1平方根课件 课件 2 次下载
- 6.3实数课件 课件 0 次下载
- 第6章实数复习课件 课件 0 次下载
- 7.1.1有序数对课件 课件 0 次下载
初中数学第六章 实数6.2 立方根精品ppt课件
展开1.了解立方根的概念,会用立方运算求一个数的立 方根;2.了解立方根的性质,并学会用计算器计算一个数 的立方根或立方根的近似值.(重点、难点)
设这种包装箱的棱长为 x m,则
这就是要求一个数,使它的立方等于 27.
因为 33 = 27,所以 x = 3.
因此这种包装箱的棱长为 3 m.
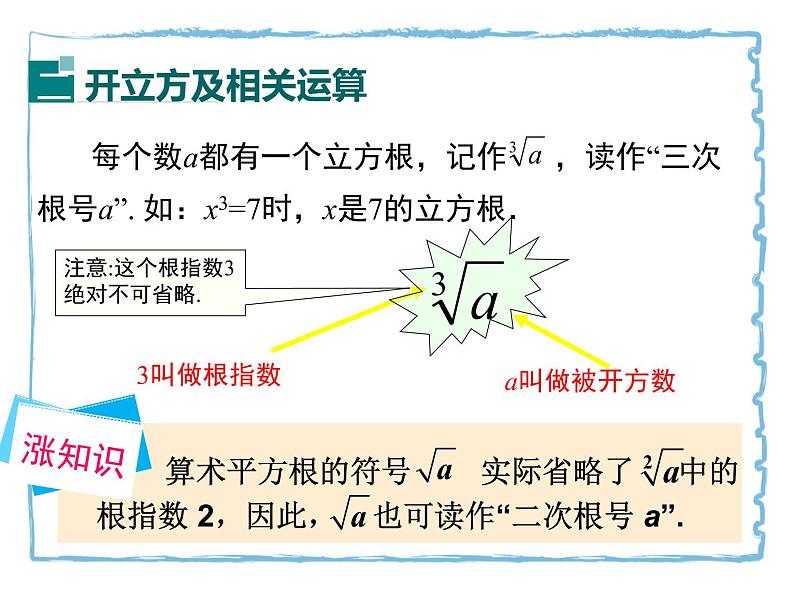
一个数a的立方根可以表示为:
其中a是被开方数,3是根指数,3不能省略.
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
填一填: 根据立方根的意义填空:
因为( )3 =0.064,所以0.064的立方是( );
因为( )3 =0,所以0的立方根是( );
因为 ( )3 =-8,所以-8的立方根是( );
一个正数有一个正的立方根;
一个负数有一个负的立方根,
立方根是它本身的数有1, -1, 0;平方根是它本身的数只有0.算术平方根是它本身的数是0,1
注意:这个根指数3绝对不可省略.
算术平方根的符号 实际省略了 中的根指数 2,因此, 也可读作“二次根号 a”.
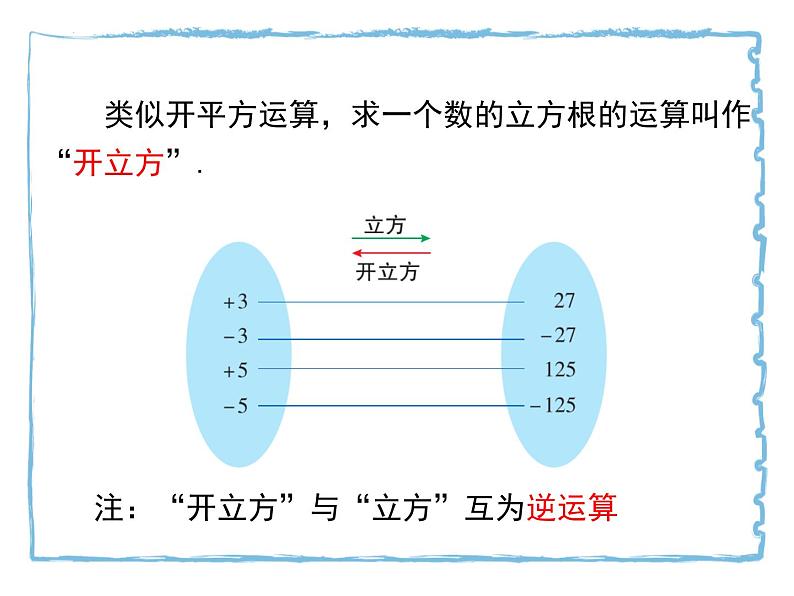
类似开平方运算,求一个数的立方根的运算叫作“开立方”.
注:“开立方”与“立方”互为逆运算
例1 求下列各数的立方根:
(5) -5的立方根是
你能归纳出立方根的另一性质吗?
平方根与立方根的区别和联系
例4 用计算器求下列各数的立方根:343,-1.331.
由于一个数的立方根可能是无限不循环小数,所以我们可以利用计算器求一个数的立方根或它的近似值.
不同的计算器的按键方式可能有所差别!
用计算器计算…, , , , ,…,你能发现什么规律?用计算器计算 (精确到0.001),并利用你发现的规律求 , , 的近似值.
小结:被开方数的小数点向左或向右移动3n位时, 立方根的小数点就相应的向左或向右移动n位 (n为正整数).
解:33 = 27,43 = 64
∵27 < 50 < 64
4.立方根概念的起源与几何中的正方体有关,如果一个正方体的体积为V,那么这个正方体的棱长为多少?
解:(1) = – 0.3
(2)
(3)
(4)
解:原式=3+2-(-1) =5+1=6.
例1 的算术平方根是 .
8.比较下列各组数的大小.
(1) 与2.5;(2) 与 .
若 =2, =4,求 的值.
解:∵ =2, =4. ∴x = 23,y2 = 16, ∴x = 8,y = ±4. ∴x + 2y = 8 + 2×4 = 16 或 x + 2y = 8 – 2×4 = 0.∴ = = 4 或 = = 0.
正数的立方根是正数,负数的立方根是负数;0的立方根是0.被开方数的小数点向左或向右移动3n位时立方根的小数点就相应的向左或向右移动n位(n为正整数).
人教版七年级下册6.2 立方根说课ppt课件: 这是一份人教版七年级下册6.2 立方根说课ppt课件,共14页。PPT课件主要包含了没有平方根,你还记得吗,立方根的定义,开立方,立方根的性质,想一想,1立方根的特征,练一练,引伸探究2,探究3等内容,欢迎下载使用。
初中数学人教版七年级下册6.2 立方根授课ppt课件: 这是一份初中数学人教版七年级下册6.2 立方根授课ppt课件,共22页。PPT课件主要包含了三次根号,根指数index,不能省略,读作三次根号a,开立方的概念,两个互为相反数,一个为正数,没有平方根,一个为负数,可以为任何数等内容,欢迎下载使用。
初中数学人教版七年级下册6.2 立方根优质课课件ppt: 这是一份初中数学人教版七年级下册6.2 立方根优质课课件ppt,共22页。PPT课件主要包含了立方根的性质,求下列各式的值,–03等内容,欢迎下载使用。













