初中数学人教版八年级下册18.2.1 矩形教学ppt课件

这是一份初中数学人教版八年级下册18.2.1 矩形教学ppt课件，共30页。PPT课件主要包含了对角线，ABCD，知识点一矩形的定义，归纳总结，知识点二矩形的性质，两组对角分别相等，对角线互相平分，形象图，你能证明吗，验证猜想1等内容，欢迎下载使用。

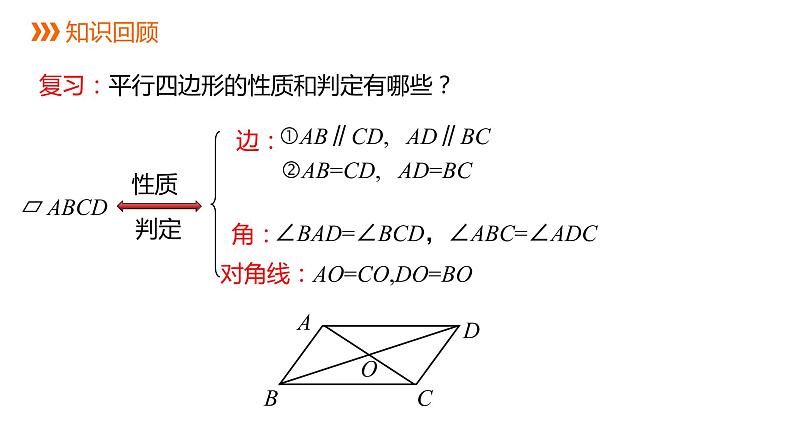
复习：平行四边形的性质和判定有哪些？
AB∥CD, AD∥BC
AB=CD, AD=BC
∠BAD=∠BCD，∠ABC=∠ADC
AO=CO,DO=BO
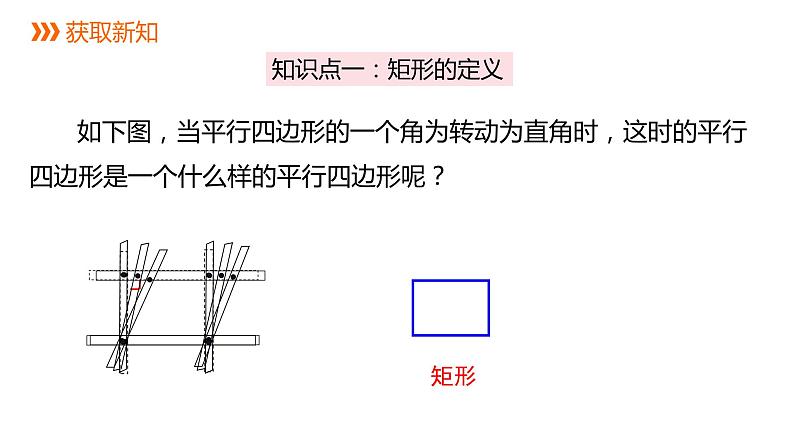
如下图，当平行四边形的一个角为转动为直角时，这时的平行四边形是一个什么样的平行四边形呢？
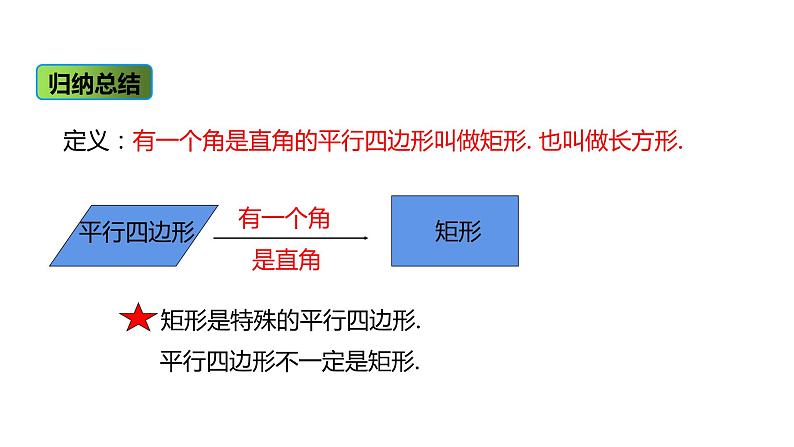
定义：有一个角是直角的平行四边形叫做矩形. 也叫做长方形.
平行四边形不一定是矩形.
矩形也是常见的图形.门窗框、教科书封面、桌面、地砖等(如下图)都有矩形的形象.你还能举出一些例子吗？
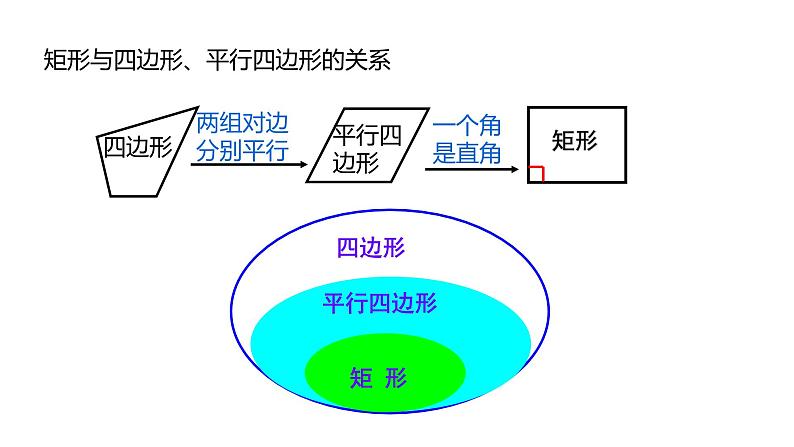
矩形与四边形、平行四边形的关系
具备平行四边形所有的性质.
两组对边平行；两组对边分别相等
因为矩形是平行四边形，所以它具有平行四边形的所有性质矩形的一般性质：
思考 它是否具有一般平行四边形不具有的一些特殊性质呢？
做一做准备素材：直尺、量角器、橡皮擦、课本、铅笔盒等.（1）请同学们以小组为单位,测量身边的矩形（如书本,课桌,铅笔盒等）的四条边长度、四个角度数和对角线的长度及夹角度数,并记录测量结果.
（2）根据测量的结果,你有什么猜想？
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
证明：∵四边形ABCD是平行四边形,∠C=90°∴∠A=∠C=90° ,∠B+∠C=180 °∴∠B=180－∠C=90°∴∠D=∠B=90° 即∠A=∠B=∠C=∠D=90°
如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证：AC=DB.
证明：∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
在△ABC和△DCB中,
∵AB=DC,∠ABC=∠DCB,BC= CB,
∴△ABC≌△DCB.
矩形除了具有平行四边形的所有性质外，还具有的性质有：矩形的四个角都是直角.矩形的对角线相等.
∵四边形ABCD是矩形，∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是矩形，∴AC=BD
矩形的两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
∵四边形ABCD是矩形,
∴AD∥BC ，CD∥AB.
∴ AD=BC ，CD =AB.
∴ AO= CO ，OD = OB.
∴ ∠A=∠B=∠C=∠D=90°.
例1 如图,在矩形ABCD中,两条对角线AC,BD相交于点O,∠AOB=60°, AB=4 ,求矩形对角线的长.
解：∵四边形ABCD是矩形， ∴AC与BD相等且互相平分.∴OA=OB.又 ∠AOB=60°，∴△OAB是等边三角形.∴OA=AB=4.∴ AC=BD=2OA=8.
矩形的对角线相等且互相平分
如图,在矩形ABCD中,E是BC上一点,AE=AD,DF⊥AE ,垂足为F.求证：DF=DC.
证明：连接DE.∵AD =AE,∴∠AED =∠ADE.∵四边形ABCD是矩形,∴AD∥BC,∠C=90°.∴∠ADE=∠DEC, ∴∠DEC=∠AED.又∵DF⊥AE, ∴∠DFE=∠C=90°.
又∵DE=DE,∴△DFE≌△DCE,∴DF=DC.
知识点三：矩形的对称性及相关性质
【思考】矩形ABCD是轴对称图形吗？
矩形是中心对称图形吗？对称中心是什么？
矩形的性质：对称性： .对称轴：.
矩形的性质：中心对称： .对称中心：.
两对全等的等腰三角形.
你在矩形中还发现了哪些基本图形？
四个全等的直角三角形.
知识点四：直角三角形斜边上中线的性质
直角三角形斜边上的中线的性质：
直角三角形斜边上的中线等于斜边的一半.
例2 如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．(1)若AB＝10，AC＝8，求四边形AEDF的周长；(2)求证：EF垂直平分AD.
证明：(2)∵DE＝AE，DF＝AF，∴E、F在线段AD的垂直平分线上， ∴EF垂直平分AD.
当已知条件含有线段的中点、直角三角形的条件时，可联想直角三角形斜边上的中线的性质进行求解．
1. 下列说法不正确的是(　　)A．矩形是平行四边形B．矩形不一定是平行四边形C．矩形的四个角都是直角D．平行四边形具有的性质矩形都具有
2. 如图,在矩形ABCD中,E是BC边的中点,且AE平分∠BAD,CE=2,则CD的长是(　　)A.2 B.3 C.4 D.5
3. 如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AO＝2，则四边形OCED的面积为(　　)A．6 B．8 C．10 D．12
4.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°,则∠DAE=　　°.
5. 如图所示,已知矩形ABCD的周长为56,O为对角线的交点,△BOC与△AOB的周长之差为4,则AB=　　,BC=　　.
6. 如图,在矩形ABCD中,BF=CE.求证:AE=DF.
证明:∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB.∵BF=CE,∴BF+EF=CE+EF,即BE=CF,∴△ABE≌△DCF(SAS),∴AE=DF.
7. 如图，已知BD，CE是△ABC不同边上的高，点G，F分别是BC，DE的中点，试说明GF⊥DE.