初中数学中考复习 专题36 几何最值之将军饮马问题【热点专题】-【中考高分导航】备战2022年中考数学考点总复习（全国通用）（原卷版）

这是一份初中数学中考复习 专题36 几何最值之将军饮马问题【热点专题】-【中考高分导航】备战2022年中考数学考点总复习（全国通用）（原卷版），共13页。
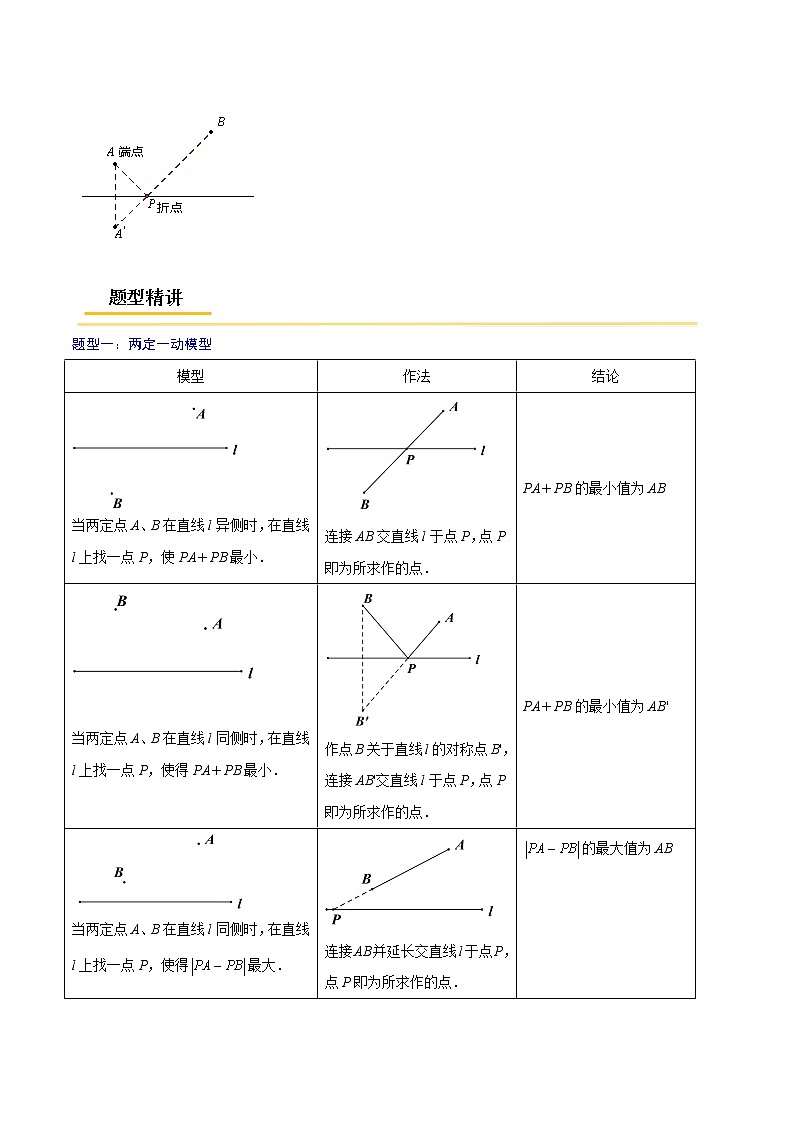
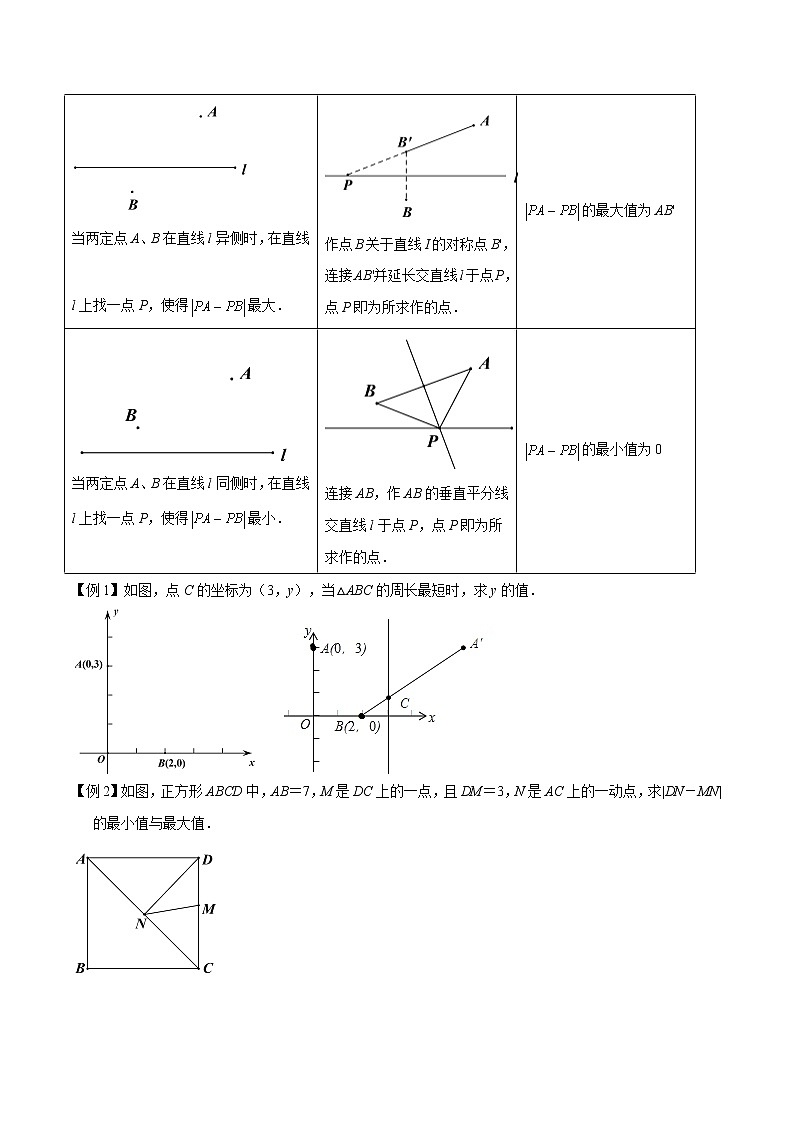
      “将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现．【抽象模型】如图，在直线上找一点P使得PA+PB最小？【模型解析】作点A关于直线的对称点A’，连接PA’，则PA’=PA，所以PA+PB=PA’+PB当A’、P、B三点共线的时候，PA’+PB=A’B，此时为最小值（两点之间线段最短）  题型一：两定一动模型模型作法结论当两定点A、B在直线l异侧时，在直线l上找一点P，使PA＋PB最小．连接AB交直线l于点P，点P即为所求作的点．PA＋PB的最小值为AB 当两定点A、B在直线l同侧时，在直线l上找一点P，使得PA＋PB最小．作点B关于直线l的对称点B'，连接AB'交直线l于点P，点P即为所求作的点．PA＋PB的最小值为AB'当两定点A、B在直线l同侧时，在直线l上找一点P，使得最大．连接AB并延长交直线l于点P，点P即为所求作的点．的最大值为AB当两定点A、B在直线l异侧时，在直线 l上找一点P，使得最大．作点B关于直线I的对称点B'，连接AB'并延长交直线l于点P，点P即为所求作的点．的最大值为AB'当两定点A、B在直线l同侧时，在直线l上找一点P，使得最小．连接AB，作AB的垂直平分线交直线l于点P，点P即为所求作的点．的最小值为0【例1】如图，点C的坐标为（3，y），当△ABC的周长最短时，求y的值．    【例2】如图，正方形ABCD中，AB＝7，M是DC上的一点，且DM＝3，N是AC上的一动点，求|DN－MN|的最小值与最大值． 【例3】如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点,,．（1）求抛物线的解析式和对称轴；（2）是抛物线对称轴上的一点，求满足的值为最小的点坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点，使四边形是以为对角线且面积为的平行四边形？若存在，请求出点坐标，若不存在请说明理由.（请在图2中探索）     题型二：一定两动模型模型作法结论 点P在∠AOB内部，在OB边上找点D，OA边上找点C，使得△PCD周长最小．分别作点P关于OA、OB的对称点P′、P″，连接P′P″，交OA、OB于点C、D，点C、D即为所求．△PCD周长的最小值为P′P″点P在∠AOB内部，在OB边上找点D，OA边上找点C，使得PD＋CD最小．作点P关于OB的对称点P′，过P′作P′C⊥OA交OB于D，点C、点D即为所求．PD＋CD的最小值为P′C【例4】如图，点P是∠AOB内任意一点，∠AOB=30°，OP=8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为___________．【例5】如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为（　　）      A．140° B．100° C．50° D．40°【例6】如图，在正方形ABCD中，点E，F分别是边AD，BC的中点，连接DF，过点E作EH⊥DF，垂足为H，EH的延长线交DC于点G．（1）猜想DG与CF的数量关系，并证明你的结论；（2）过点H作MN∥CD，分别交AD，BC于点M，N，若正方形ABCD的边长为10，点P是MN上一点，求△PDC周长的最小值．    【例7】如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．（1）求抛物线的解析式及点D的坐标；（2）当△CMN是直角三角形时，求点M的坐标；（3）试求出AM+AN的最小值．      题型三：两定两动模型模型作法结论点P、Q在∠AOB内部，在OB边上找点D，OA边上找点C，使得四边形PQDC周长最小．分别作点P、Q关于OA、OB的对称点P′、Q′，连接P′Q′，分别交OA、OB于点C、D，点C、D即为所求．PC＋CD＋DQ的最小值为P′Q′，所以四边形PQDC周长的最小值为PQ＋P′Q′【例8】如图，在矩形中， ， ，为的中点，若为边上的两个动点，且，若想使得四边形的周长最小，则的长度应为__________.【例9】如图，已知直线l1∥l2，l1、l2之间的距离为8，点P到直线l1的距离为6，点Q到直线l2的距离为4，PQ=，在直线l1上有一动点A，直线l2上有一动点B，满足AB⊥l2，且PA+AB+BQ最小，此时PA+BQ=______．题型四：两定点一定长模型作法结论如图，在直线l上找M、N两点(M在左)，使得AM＋MN＋NB最小，且MN＝d. 将A向右平移d个单位到A′，作A′关于l的对称点A"，连接A"B与直线l交于点N，将点N向左平移d个单位即为M，点M，N即为所求. AM＋MN＋NB的最小值为A"B＋d 如图，l1∥l2，l1、l2间距离为d，在l1、l2分别找M、N两点，使得MN⊥l1，且AM＋MN＋NB最小． 将A向下平移d个单位到A，连接A′B交直线l2于点N，过点N作MN⊥l1，连接AM.点M、N即为所求． AM＋MN＋NB的最小值为A'B＋d. 【例10】在平面直角坐标系中，矩形OABC如图所示，点A在x轴正半轴上，点C在y轴正半轴上，且OA＝6，OC＝4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF＝2.当四边形BDEF的周长最小时，求点E的坐标．         【例11】村庄A和村庄B位于一条小河的两侧，若河岸彼此平行，要架设一座与河岸垂直的桥，桥址应如何选择，才使A与B之间的距离最短？     1．如图，在Rt△ABC中，∠ACB=90°，AC=6．AB=12，AD平分∠CAB，点F是AC的中点，点E是AD上的动点，则CE+EF的最小值为　　A．3 B．4 C． D．2．如图，在锐角三角形ABC中，BC=4，∠ABC=60°， BD平分∠ABC，交AC于点D，M、N分别是BD，BC上的动点，则CM+MN的最小值是　　A． B．2 C． D．43．如图，在正方形ABCD中，AB=9，点E在CD边上，且DE=2CE，点P是对角线AC上的一个动点，则PE+PD的最小值是（　　）A． B． C．9 D．4．如图，在正方形ABCD中，E是AB上一点，BE＝2，AB＝8，P是AC上一动点，则PB+PE的最小值_____．5．如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（3，0）是OB上的一定点，点M是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为______．6．如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE＝2，当EF＋CF取得最小值时，则∠ECF的度数为多少？       7．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，A(3，0)，B(0，4)，D为边OB的中点．（1）若E为边OA上的一个动点，求△CDE的周长最小值；（2）若E、F为边OA上的两个动点，且EF＝1，当四边形CDEF的周长最小时，求点E、F的坐标．   8．如图所示抛物线过点，点，且（1）求抛物线的解析式及其对称轴；（2）点在直线上的两个动点，且，点在点的上方，求四边形的周长的最小值；（3）点为抛物线上一点，连接，直线把四边形的面积分为3∶5两部分，求点的坐标.  9．如图，在平面直角坐标系中，矩形的边交轴于点，轴，反比例函数的图象经过点，点的坐标为，．（1）求反比例函数的解析式；（2）点为轴上一动点，当的值最小时，求出点的坐标．     10．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．