内蒙古阿拉善盟2022-2023学年高三上学期期末考试数学（理科）试题

阿拉善盟2022-2023学年高三上学期期末考试

数学（理科）

考生注意：

1.本试卷分选择题和非选择题两部分。满分150分，考试时间120分钟。

2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3.考生作答时，请将答案答在答题卡上。选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效。

4.本卷命题范围：高考范围。

一、选择题：本题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1.记集合，，则（    ）

A.  B.或

C.  D.

2.已知复数（i是虚数单位），则（    ）

A. B. C. D.

3.命题“，x是奇函数”的否定是（    ）

A.，是偶函数 B.，不是奇函数

C.，是偶函数 D.，不是奇函数

4.若，则（    ）

A. B. C. D.

5.若双曲线（）的渐近线与圆相切，则（    ）

A. B. C. D.

6.端午节为每年农历五月初五，又称端阳节、午日节、五月节等.端午节是中国汉族人民纪念屈原的传统节日，以围绕才华横溢、遗世独立的楚国大夫屈原而展开，传播至华夏各地，民俗文化共享，屈原之名人尽皆知，追怀华夏民族的高洁情怀.小华的妈妈为小华煮了8个粽子，其中5个甜茶粽和3个艾香粽，小华随机取出两个，事件A“取到的两个为同一种馅”，事件B“取到的两个都是艾香粽”，则（    ）

A. B. C. D.

7.正方体中，E为的中点，则异面直线与所成角的余弦值为（    ）

A. B. C. D.

8.某地锰矿石原有储量为a万吨，计划每年的开采量为本年年初储量的m（，且m为常数）倍，第n（）年开采后剩余储量为，按该计划使用10年时间开采到剩余储量为原有储量的一半.若开采到剩余储量为原有储量的70%，则需开采约（参考数据：）（    ）

A.3年 B.4年 C.5年 D.6年

9.在平行四边形中，，，，，且，则平行四边形的面积为（    ）

A. B. C. D.

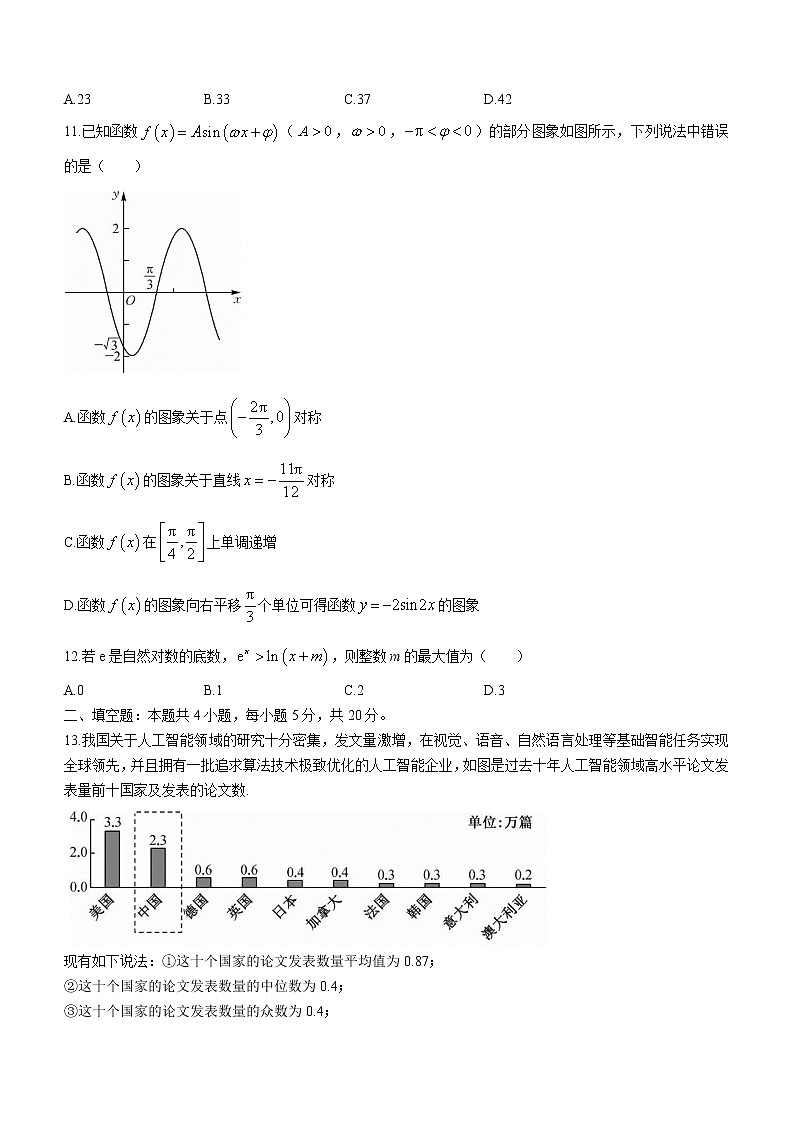
10.更相减损术是出自中国古代数学专著《九章算术》的一种算法，其内容如下：“可半者半之，不可半者，副置分母、子之数，以少减多，更相减损，求其等也，以等数约之”，如图是该算法的程序框图，如果输入，，则输出的a是（    ）

A.23 B.33 C.37 D.42

11.已知函数（，，）的部分图象如图所示，下列说法中错误的是（    ）

A.函数的图象关于点对称

B.函数的图象关于直线对称

C.函数在上单调递增

D.函数的图象向右平移个单位可得函数的图象

12.若e是自然对数的底数，，则整数m的最大值为（    ）

A.0 B.1 C.2 D.3

二、填空题：本题共4小题，每小题5分，共20分。

13.我国关于人工智能领域的研究十分密集，发文量激增，在视觉、语音、自然语言处理等基础智能任务实现全球领先，并且拥有一批追求算法技术极致优化的人工智能企业，如图是过去十年人工智能领域高水平论文发表量前十国家及发表的论文数.

现有如下说法：①这十个国家的论文发表数量平均值为0.87；

②这十个国家的论文发表数量的中位数为0.4；

③这十个国家的论文发表数量的众数为0.4；

④德国发表论文数量约占美国的32%.

其中正确的是___________.（填序号）

14.如图，中华中学某班级课外学习兴趣小组为了测量某座山峰的高气度，先在山脚A处测得山顶C处的仰角为60°，又利用无人机在离地面高400m的M处（即），观测到山顶C处的仰角为15°，山脚A处的俯角为45°，则山高___________m.

15.在三棱锥中，是等边三角形，平面平面，，，且三棱锥的所有顶点都在半径为4的球O的球面上，则三棱锥的体积为___________.

16.已知椭圆C：（）的左、右焦点分别为，，C的下顶点为A，离心率为，过且垂直于的直线与C交于D，E两点，，则的周长为___________.

三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。

（一）必考题：共60分。

17.（本小题满分12分）

已知数列的前n项和.

（1）求；

（2）令，若对于任意，数列的前n项和恒成立，求实数m的取值范围.

18.（本小题满分12分）

盲盒里面通常装的是动漫、影视作品的周边，或者设计师单独设计出来的玩偶.由于盒子上没有标注，购买者只有打开后才会知道自己买到了什么，因此这种惊喜吸引了众多年轻人，形成了“盲盒经济”.某款盲盒内装有正版海贼王手办，且每个盲盒只装一个.某销售网点为调查该款盲盒的受欢迎程度，随机抽取了400人进行问卷调查，并全部收回.经统计，有30%的人购买了该款盲盒，在这些购买者当中，男生占一；而在未购买者当中，男生、女生各占50%.

（1）完成下面的列联表，并判断是否有99.5%的把握认为是否购买该款盲盒与性别有关？

（2）从购买该款盲盒的人中按性别用分层抽样的方法随机抽取6人，再从这6人中随机抽取3人发放优惠券，记X为抽到的3人中女生的人数，求X的分布列和数学期望.

参考公式：，其中.

参考数据：

19.（本小题满分12分）

如图，在直四棱柱中，四边形是菱形，，，，点E是棱上的一点（与B，不重合）.

（1）求证：；

（2）若二面角的余弦值为，求直线与平面所成角的正弦值.

20.（本小题满分12分）

已知抛物线C：（）的焦点为F，过点的直线l与C相交于A，B两点.当直线l经过点Ｆ时，点A恰好为线段的中点.

（1）求C的方程；

（2）是否存在定点T，使得为常数？若存在，求出点T的坐标及该常数；若不存在，说明理由.

21.（本小题满分12分）

设向量，，，（）.

（1）讨论函数的单调性；

（2）设函数，若存在两个极值点，（），证明：.

（二）选考题：共10分。请考生在第22、23两题中任选一题作答。如果多做，则按所做的第一题计分。

22.（本小题满分10分）选修4-4：坐标系与参数方程

在直角坐标系中，曲线C的参数方程为（t为参数），以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为.

（1）求l的直角坐标方程；

（2）若l与C有公共点，求m的取值范围.

23.（本小题满分10分）选修4-5：不等式选讲

已知，，，且.

证明：（1）；

（2）.

阿拉善盟2022-2023学年高三上学期期末考试

数学（理科）

参考答案、提示及评分细则

1.B  集合或，或，所以或.故选B.

2.A  由题意知，故选A.

3.B  命题“，是奇函数”的否定是：，不是奇函数.故选B.

4.C  由，得，所以.故选C.

5.D  双曲线（）的渐近线为，即.不妨取，圆，即，所以圆心为，半径，依题意圆心到渐近线的距离，解得或（舍去）.故选D.

6.B  由题意，，，所以.故选B.

7.A  平移到，再连接，则或其补角为异面直线与所成的角，设正方体的棱长为2，易得，，，由余弦定理得.故选A.

8.C  设第n年开采后剩余储量为y，则，当时，，所以，，故，进而，设第n年时，，故，故.故选C.

9.A  因为，，所以，解得，则，所以.故选A.

10.B  根据程序框图，输入的，，因为，且，所以；第二次循环，；第三次循环，；第四次循环，，此时，输出.故选B.

11.D  易得，即，所以，将代入得，所以.对于A选项，令，，解得，，对称中心为，，当时，对称中心为，故A正确；对于B选项，根据，，解得，，当时，，故B正确；对于C选项，由，得的单调递增区间为，，又，，故C正确；对于D选项，函数图象上所有的点向右平移个单位，得到函数，故D错误.故选D.

12.C  令，则等价于，即，从而.设，则.易知在上单调递增，且，.所以存在唯一的，使得，即，则.当时，，在上单调递减；当时，，在上单调递增.从而，而在上是减函数，所以.因此的最小值，从而整数的最大值是2.故选C.

13.①②  结合图表易得该组数据的众数为0.3，德国发表论文数量约占美国的18%，故只有①②正确.

14.600  由题意知，则，又由，所以，，在中，由正弦定理得，即，解得，则.

15.24  因为，所以为所在截面圆的直径，又平面平面，为等边三角形，所以O在上，如图所示.设（），则，，所以，解得，所以，，又，，所以，所以.

16.  因为C的离心率，所以，，所以C的方程为，即.在中，，，所以为正三角形.过且垂直于的直线与C交于D，E两点，所以为线段的垂直平分线，直线的斜率为，所以直线的方程为.设，，由得，所以，，所以，解得，所以.因为为线段的垂直平分线，所以，，所以的周长为.

17.解：（1）当时，；·································································2分

当时，.

∵不满足上式，∴····································································5分

（2）由（1）可得，··································································.6分

当时，，···········································································8分

∴

，················································································10分

又恒成立，

∴，

即实数m的取值范围为.································································12分

18.解：（1）

··················································································2分

根据列联表中的数据，可得，····························································4分

因为，所以有99.5%的把握认为是否购买该款盲盒与性别有关.····································6分

（2）抽取6人中，女生有：（人），男生有：（人）.

X的所有可能取值为1，2，3，···························································7分

，，，

所以X的分布列为：

·················································································10分

所以.·············································································12分

19.（1）证明：连接，，如图所示.因为四边形是菱形，所以，···································1分

因为直四棱柱，所以平面，又平面，所以，·················································2分

又，，平面，所以平面，·······························································4分

又平面，所以.·······································································5分

（2）解：记与的交点为O，连接交于点.

以O为坐标原点，分别以，，所在的直线为x轴，y轴，x轴建立空间直角坐标系，如图所示，所以，，，，设（），故，

所以，，，.

设平面的一个法向量，所以

令，解得，，所以平面的一个法向量.······················································6分

设平面的一个法向量，所以

令，解得，，所以平面的一个法向量，·····················································7分

所以，·············································································9分

解得，············································································10分

所以平面的一个法向量为.

设直线与平面所成的角为，所以，

所以直线与平面所成角的正弦值为.·······················································12分

20.解：（1）因为，，且点A恰好为线段中点，所以，··········································1分

又因为A在C上，所以，即，·····························································3分

解得，所以C的方程为.·································································4分

（2）设，由题意可知直线l斜率存在，设直线l的方程为，，，

由得，所以，，······································································6分

所以

.··················································································9分

令················································································10分

解得即，··········································································11分

此时.·············································································12分

21.（1）解：根据已知得，，则

，·················································································1分

若，当时，；当时，，

所以在上单调递减，在上单调递增.·······················································.2分

若，由，得或；由，得，

所以在，上单调递增，在上单调递减.······················································3分

若，恒成立，所以在上单调递增.·························································4分

若，由，得或；由，得，

所以在，上单调递增，在上单调递减..······················································5分

（2）证明：由已知得，从而，.··························································6分

当时，恒成立，函数不可能有两个极值点；

当时，有两个根，，因为，与，都是正数相矛盾，不合题意；

··················································································7分

当时，有两个根，，因为，且，所以两根，均为正数，故有两个极值点，···························8分

因为，由知，，

因为，

所以等价于，

即.···············································································10分

令（），，

所以在上单调递减，又，所以当时，.

故成立.············································································12分

22.解：（1）因为l：，所以，

又因为，，得，

即l的直角坐标方程为.··································································3分

（2）将代入中，得，

所以，即，

要使l与C有公共点，则有解，即有解.······················································5分

令，则，令，，所以在上单调递减，在上单调递增，所以，

又，，

所以，·············································································8分

解得，即m的取值范围是.······························································10分

23.证明，（1）因为，，，则，，，

所以，即，所以，

当且仅当，即时取等号.································································5分

（2）因为，，，所以，，，

所以，，，

所以，

当且仅当，即时取等号.································································10分