初中数学湘教版八年级下册第1章 直角三角形1.3 直角三角形全等的判定图片ppt课件

这是一份初中数学湘教版八年级下册第1章 直角三角形1.3 直角三角形全等的判定图片ppt课件，共13页。PPT课件主要包含了ASA，BCEF，知识回顾，两个直角三角形呢，这两个三角形全等吗，疑问升级，例题讲解，连结AB，答不对，随堂练习等内容，欢迎下载使用。
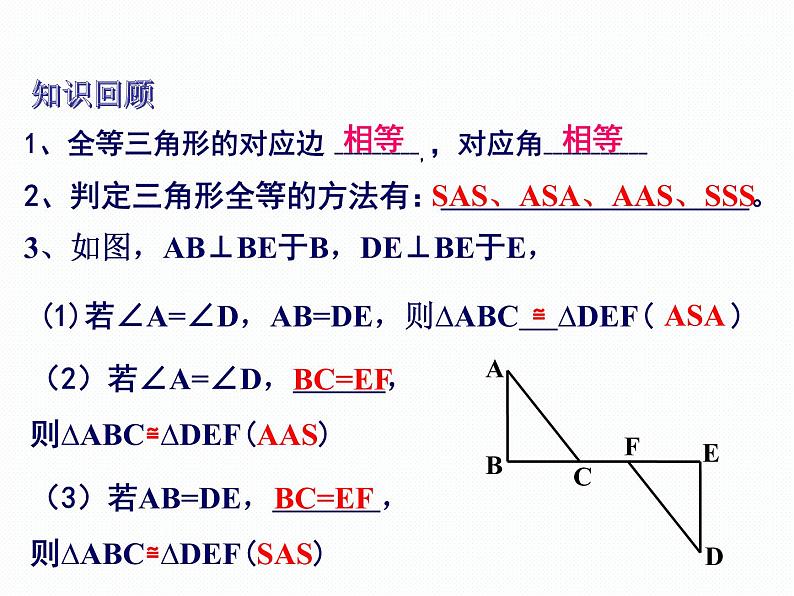
1、全等三角形的对应边 ---------,，对应角-----------
2、判定三角形全等的方法有： 。
SAS、ASA、AAS、SSS
(1)若∠A=∠D，AB=DE，则∆ABC ∆DEF( )
3、如图，AB⊥BE于B，DE⊥BE于E，
（2）若∠A=∠D， ，则∆ABC≌∆DEF(AAS)
（3）若AB=DE， ，则∆ABC≌∆DEF(SAS)
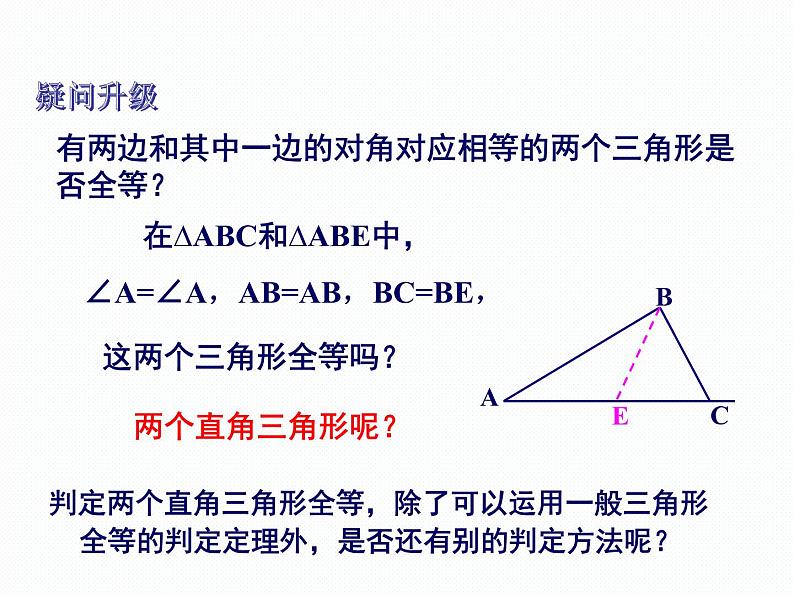
有两边和其中一边的对角对应相等的两个三角形是否全等？
在∆ABC和∆ABE中，
∠A=∠A，AB=AB，BC=BE，
判定两个直角三角形全等，除了可以运用一般三角形全等的判定定理外，是否还有别的判定方法呢？
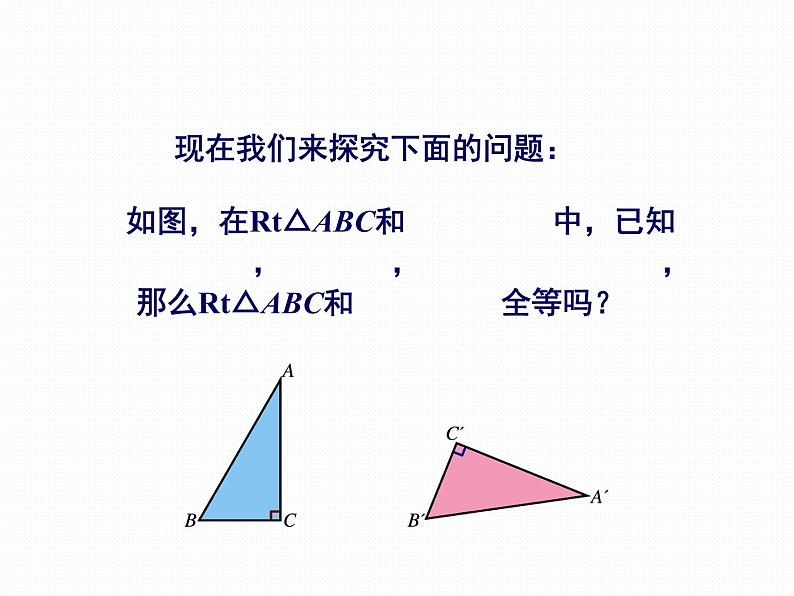
现在我们来探究下面的问题：
1、你能把这两个三角形通过平移、旋转或轴反射等变换拼接成一个等腰三角形吗？
2、从上面的操作中，你能猜测这两个直角三角形全等吗？
证明：因为∠ACB = 90°.
由于 ， ∠B = ∠B’， ，
所以∠BCB′=∠ACB+∠ACB′=180°.故B，C，(C′)，B′在同一条直线上.
因为 AB=A′B′=AB′，所以 ∠B=∠B’ . (等边对等角)
3、请用推理的方法说明你猜想的正确性。
直角三角形全等的判定定理：
斜边、直角边定理 有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).
4、你能用语言概括上面发现的结论吗？
这个定理的条件，实际就是已知两边和其中一边的对角对应相等，在前面已经探究过，具备这样条件的两个一般三角形并不一定全等.
例1、如图，BD、CE分别是∆ABC的高，且BE=CD。求证：Rt∆BEC≌Rt∆CDB
证明：∵ BD、CE分别是∆ABC的高，
∴ ∠BEC=∠CDB=90°
在Rt∆BEC和Rt∆CDB中∵ BC=CB BE=CD∴Rt∆BEC≌Rt∆CDB(HL)
本题还能证明出其他的结论吗？与同学讨论交流。
已知线段a、c(a