初中数学湘教版八年级下册1.4 角平分线的性质说课ppt课件

这是一份初中数学湘教版八年级下册1.4 角平分线的性质说课ppt课件，共13页。PPT课件主要包含了知识回顾，你能证明吗，作射线OC．，疑问升级，用符号语言表示为，角平分线的性质，新知探究，∠ABD∠CBD，例题讲解，∠1∠2等内容，欢迎下载使用。
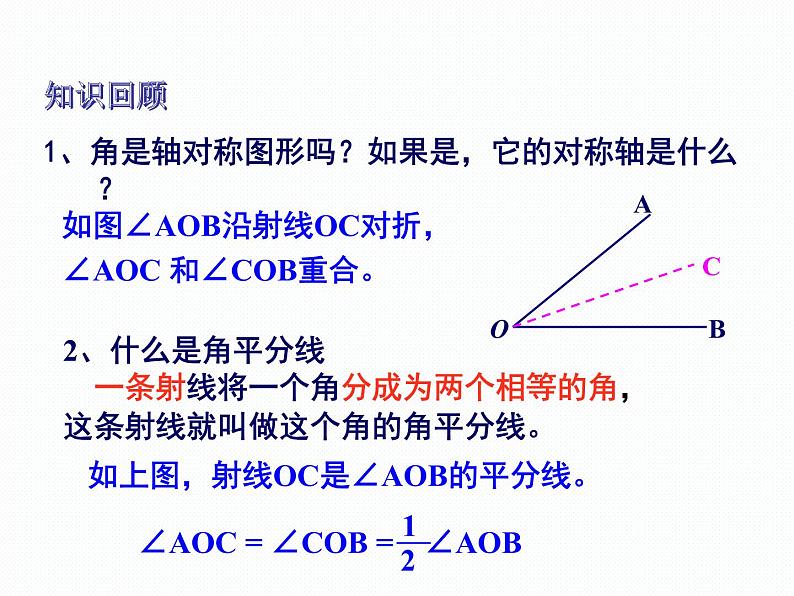
1、角是轴对称图形吗？如果是，它的对称轴是什么？
2、什么是角平分线 一条射线将一个角分成为两个相等的角，这条射线就叫做这个角的角平分线。
如图∠AOB沿射线OC对折，∠AOC 和∠COB重合。
如上图，射线OC是∠AOB的平分线。
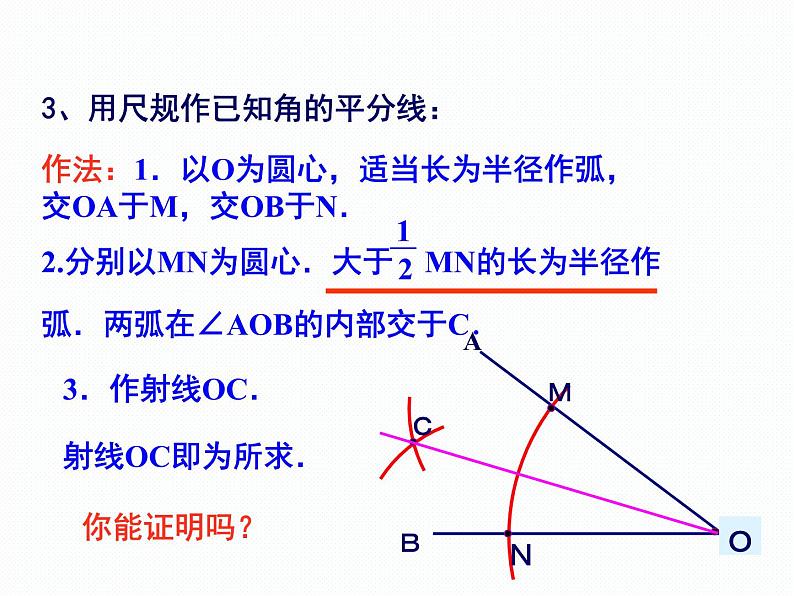
3、用尺规作已知角的平分线：
作法：1．以O为圆心，适当长为半径作弧，交OA于M，交OB于N．
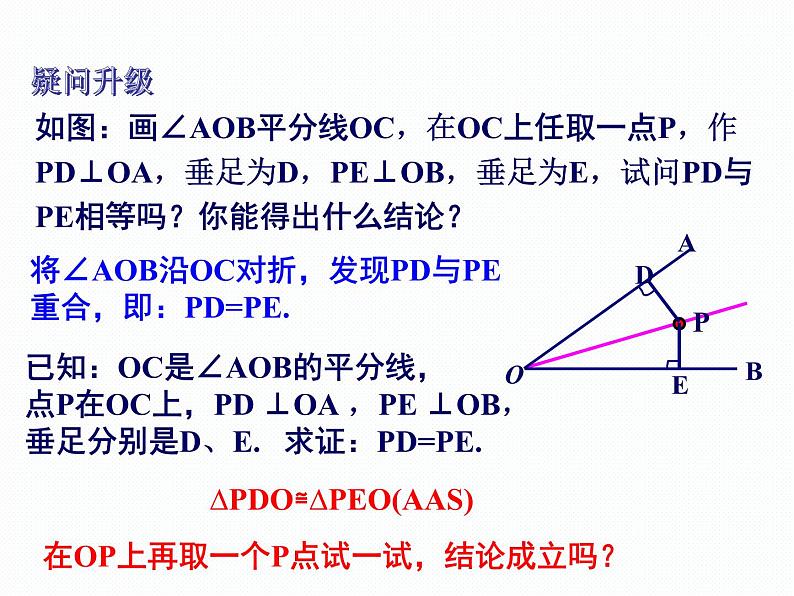
如图：画∠AOB平分线OC，在OC上任取一点P，作PD⊥OA，垂足为D，PE⊥OB，垂足为E，试问PD与PE相等吗？你能得出什么结论？
∆PDO≌∆PEO(AAS)
在OP上再取一个P点试一试，结论成立吗？
将∠AOB沿OC对折，发现PD与PE重合，即：PD=PE.
已知：OC是∠AOB的平分线，点P在OC上，PD ⊥OA ，PE ⊥OB，垂足分别是D、E. 求证：PD=PE.
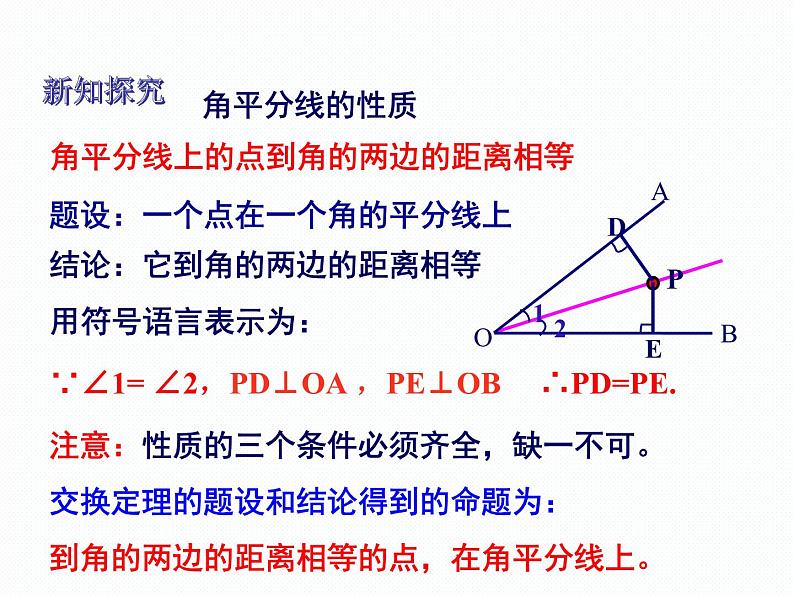
角平分线上的点到角的两边的距离相等
题设：一个点在一个角的平分线上
结论：它到角的两边的距离相等
∵∠1= ∠2，PD⊥OA ，PE⊥OB ∴PD=PE.
交换定理的题设和结论得到的命题为：
到角的两边的距离相等的点，在角平分线上。
注意：性质的三个条件必须齐全，缺一不可。
角的内部到角的两边距离相等的点，在角平分线上。
∵PD ⊥OA ，PE ⊥OB，PD=PE∴ ∠1= ∠2 .
分析：如何量化表示结论？（连接OP，证明∠1= ∠2 .则OP是角平分线，即点P在∠AOB的平分线上）
证明：Rt∆PDO≌Rt∆PEO(HL)即可
角的平分线是到角的两边距离相等的所有点的集合.
如图：已知P点是∠AOB内一点，PD ⊥OA ，PE ⊥OB，垂足分别是D、E，且PD=PE. 求证： 点P在∠AOB的平分线上。
1、如图，∠BAD= ∠BCD=900 ，∠1= ∠2 .（1）求证：点B在∠ADC的平分线上 .（2）求证：BD是∠ABC的平分线 .
证明：（1） ∵∠1= ∠2 ∴ BA=BC，
∴点B在∠ADC的平分线上
（2）在Rt∆BAD和Rt∆BCD中，
∵ BA=BC BD=BD
∴ Rt∆BAD≌Rt∆BCD (HL)
∴ BD是∠ABC的平分线
∵∠BAD= ∠BCD=900， BA ⊥AD，BC ⊥CD
例2、如图，在Rt△ABC 中，∠C=90°，BD是∠AB C的平分线 ，DE⊥AB，垂足为E，图中相等的线段有哪些？为什么？
∵ ∠C=90° （已知）∴ DC⊥BC（垂直的定义）又∵ BD是∠ABC的平分线∵ DE⊥BA（已知）∴ DE=DC（角平分线上的任意点到角的两边的距离相等）
答： (1) DE=DC
角平分线的性质，为我们证明两线段相等 又提供了新的方法与途径
做完本题后，你对角平分线,又增加了什么认识?
1、填空：(1) ∵∠1= ∠2，DC⊥AC， DE⊥AB ∴___________(____________________________________)(2) ∵DC⊥AC ，DE⊥AB ，DC=DE∴__________（ ）
到角的两边的距离相等的点在角平分线上。
(3)如图所示，在△ABC中，∠C=90°，AD是∠BAC的平分线交BC于D，BC=15，且DB=10，则点D到AB的距离为 。
(3)∵ AD平分∠BAC, DC⊥AC，DB⊥AB （已知） ∴ BD = CD ， （ ）
（2）∵ 如图，DC⊥AC，DB⊥AB （已知）∴ BD = CD，( )
2、判断以下所填结论是否正确：
（1）∵ 如图，AD平分∠BAC（已知）∴ BD= CD ( )
3.如图，△ABC中，∠A=90°，BD平分∠ABC，AD=6，BC=16，DE⊥BC，求△BDC面积。
∴ DE=AD=6（角平分线上的任意点到角的两边的距离相等）
解：∵ ∠A=90° （已知）
∴ DA⊥AB（垂直的定义）
又∵ BD是∠ABC的平分线
∵ DE⊥BA DE⊥BC（已知）
4.已知：如图，∠C=∠D=90° ，AC=AD .求证:（1） ∠ABC= ∠ABD ；（2）BC=BD.（要求不用三角形全等的判定）
证明： (1)∵∠C= ∠D=90°，∴∆BAD和∆BCD均为直角三角形，
又∵AC= AD，AB=AB∴Rt∆BAD≌Rt∆BCD (HL)
∴∠ABC= ∠ABD
（2）由（1）得： ∠CAB= ∠DAB
即：AB是∠CAD的平分线
∵∠C= ∠D=90°，即：BC⊥AC，BD⊥AD