





初中数学湘教版七年级下册1.2.1 代入消元法教学课件ppt
展开
这是一份初中数学湘教版七年级下册1.2.1 代入消元法教学课件ppt,共20页。PPT课件主要包含了知识要点,y20,x40,x+y60,解得y20,代入xy+20,得x40,二元一次方程组,一元一次方程,根据题意可列方程组等内容,欢迎下载使用。
用代入法解二元一次方程组
1.什么是二元一次方程的解?使二元一次方程两边的值相等的两个未知数的值,叫作二元一次方程的解.2.什么是二元一次方程组的解?在二元一次方程组中,使每一个方程的左、右两边的值都相等的一组未知数的值,叫做二元一次方程组的解.
在上一节中,我们列出了二元一次方程组
并且知道x=40,y=20是这个方程组的一个解.这个解是怎么得到的呢?
大家都会解一元一次方程,可是现在方程①和方程②中都含有两个未知数,该如何解决呢?
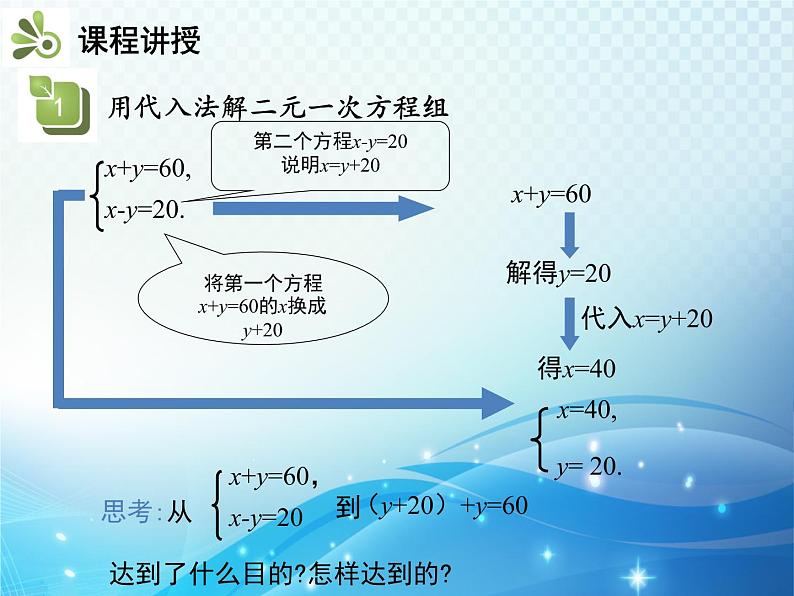
方程①和②中的x都表示一月份的天然气费,y都表示一月份的水费,因此方程中②中的x,y分别与方程①中的x,y的值相同.由②式,可得 x=y+20. ③于是可以把③代入①式,得 (y+20)+y=60, ④解方程④,得 .把y的值代入③式,得 .因此原方程组的解是
x+y=60,x-y=20.
第二个方程x-y=20说明x=y+20
将第一个方程x+y=60的x换成y+20
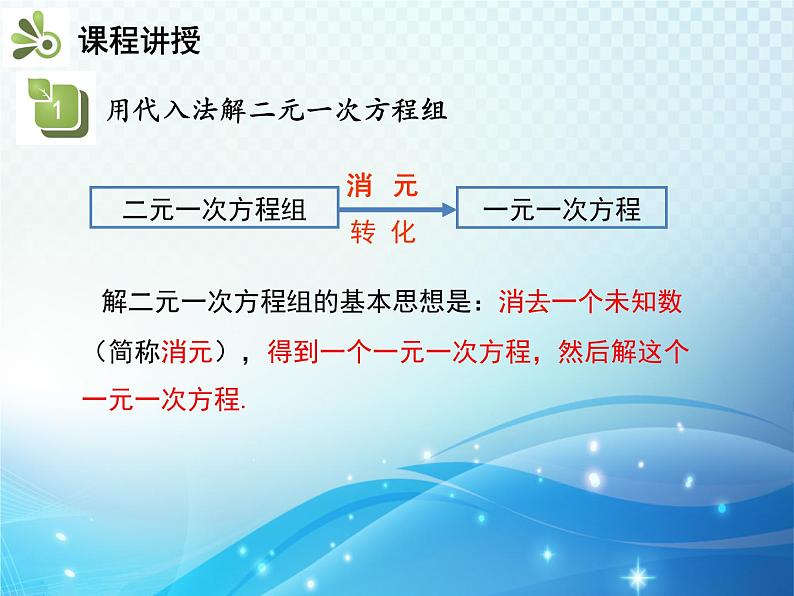
解二元一次方程组的基本思想是:消去一个未知数(简称消元),得到一个一元一次方程,然后解这个一元一次方程.
在上面的例子中,消去一个未知数的方法是:把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法叫作代入消元法,简称代入法.
解:由②式,得 y= -3x+1. ③ 把③代入①式,得5x-(-3x+1)=-9. 解得 x= -1. 把x= -1代入③式,得 y=4. 因此原方程组的解是
用代入法解方程组 较简单的方法是( ) A.消y B.消x C.消x和消y一样 D.无法确定
根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
解:设这些消毒液应该分装x大瓶、y小瓶.
解得 x=20 000
答:这些消毒液应该分装20 000大瓶和50 000小瓶.
上面解方程组的过程可以用下面的框图表示:
y=2x, x+y=12;
2x=y-5,4x+3y=65.
3.有甲、乙两种货车,3辆甲种货车与4辆乙种货车 一次可运货23 t,1辆甲种货车与5辆乙种货车一 次可运货15 t.求甲、乙两种货车每辆一次分别可 运货多少吨.
解:设甲种货车每辆一次可运货x t,乙种货车每 辆一次可运货y t.
答:甲种货车每辆一次可运货5吨,乙种货车每辆一次可运货2 t.
相关课件
这是一份湘教版七年级下册第1章 二元一次方程组1.2 二元一次方程组的解法1.2.1 代入消元法教学ppt课件,共26页。PPT课件主要包含了由②式可得,二元一次方程组,解方程④得,因此原方程组的解是,一元一次方程,12x-y﹣1,代入消元法,解由①式可得,将③代入②得,解得x5等内容,欢迎下载使用。
这是一份数学1.2.1 代入消元法完整版课件ppt,文件包含121代入消元法课件pptx、121代入消元法教案doc等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
这是一份初中第1章 二元一次方程组1.2 二元一次方程组的解法1.2.1 代入消元法精品ppt课件,文件包含七年级数学下册121代入消元法湘教版pptx、湘教版七下数学121代入消元法教案doc等2份课件配套教学资源,其中PPT共27页, 欢迎下载使用。










