2023年中考数学专项汇编 【函数】题型精练 一次函数

这是一份2023年中考数学专项汇编 【函数】题型精练 一次函数，共24页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
 一次函数（精练）
A基础训练 B能力提升
A基础训练
一、单选题
1．（2022春·陕西宝鸡·八年级统考期中）将直线向右平移2个单位后，所得直线解析式为（　　）
A． B． C． D．
2．（2022春·全国·八年级专题练习）一次函数的图象如图所示，则关于x的方程的解为（　　）

A． B． C． D．
3．（2022春·全国·八年级专题练习）一次是常数的图象如图所示，则关于x的方程的是（　　）

A．x＝3 B．x＝4 C．x＝0 D．x＝b
4．（2022春·全国·八年级专题练习）如图，两个一次函数图像的交点坐标为，则关于，的方程组的解为（　　）

A． B． C． D．
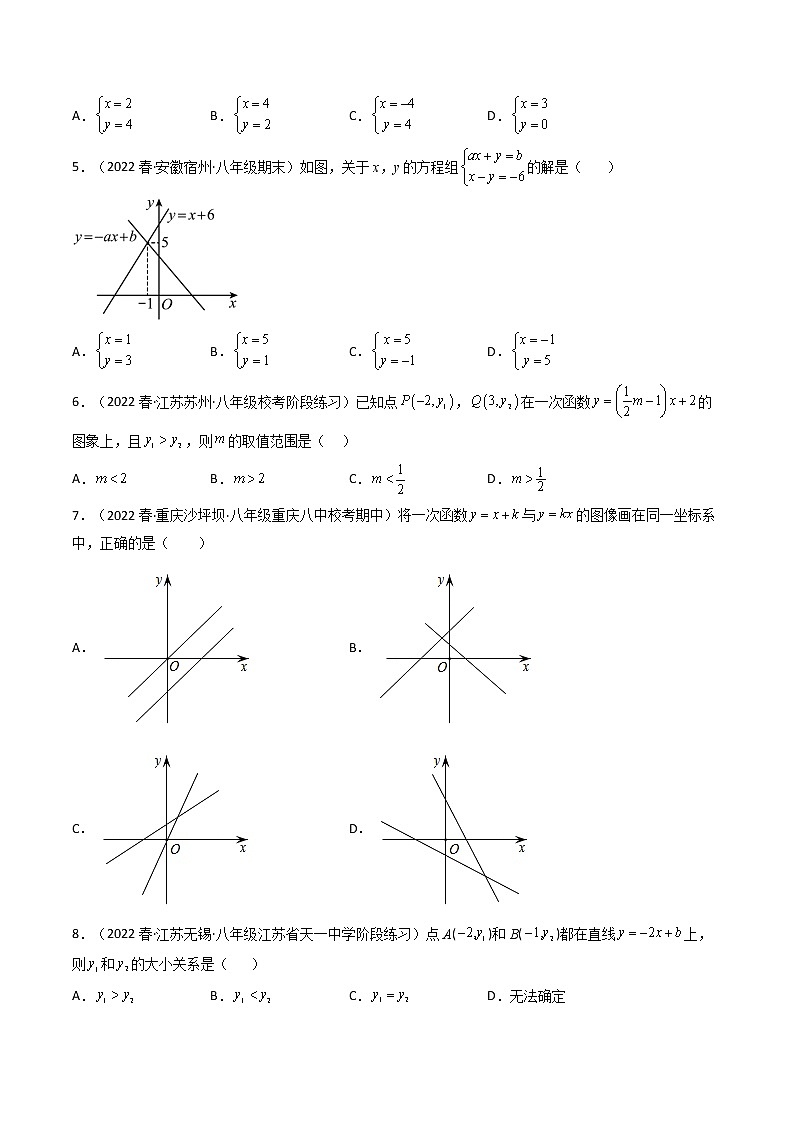
5．（2022春·安徽宿州·八年级期末）如图，关于x，y的方程组的解是（      ）

A． B． C． D．
6．（2022春·江苏苏州·八年级校考阶段练习）已知点，在一次函数的图象上，且，则的取值范围是（    ）
A． B． C． D．
7．（2022春·重庆沙坪坝·八年级重庆八中校考期中）将一次函数与的图像画在同一坐标系中，正确的是（　　）
A． B．
C． D．
8．（2022春·江苏无锡·八年级江苏省天一中学阶段练习）点A()和B()都在直线上，则和的大小关系是（  　）
A． B． C． D．无法确定
9．（2022春·八年级单元测试）对于函数，下列结论正确的是（    ）
A．它的图象必经过点 B．它的图象经过第一、二、三象限
C．当时， D．的值随值的增大而增大
10．（2022春·广东深圳·八年级统考期末）己知一次函数，y随着x的增大而减小，则在直角坐标系内它的大致图象是（  ）
A． B．
C． D．
11．（2022春·陕西西安·八年级校考期中）一次函数与的图象在同一坐标系中可能是（　　）
A． B．
C． D．
12．（2022春·重庆万州·九年级重庆市万州第二高级中学期末）网语期印，李明同学在老家学习生活，为缓解线上学习疲劳，在某个周末和爸爸进行登山锻炼，登山过程中，两人距地面的高度y(米)与登山时间x(分钟)之间的函数图像如图所示(甲为爸爸，乙为李明)，李明提速后，李明的登山速度是原来速度的2倍，并先到达山顶.根据图象所提供的信息，下列说法情误的是（  ）

A．甲登山的速度是每分钟米
B．乙在A地时距地面的高度b为米
C．乙登山分钟时追上甲
D．登山时间为5分钟、8分钟、分钟时，甲、乙两人距地面的高度差为米
13．（2022春·浙江杭州·九年级萧山区党湾镇初级中学校考期中）将二次函数的图象向右平移1个单位，再向上平移2个单位后，顶点在直线上，则k的值为（    ）
A．2 B．1 C．0 D．
14．（2022春·全国·八年级专题练习）已知直线与直线交于点P，且点P的横坐标为3，下列结论：
①关于x的方程的解为；
②对于直线，当时，；
③方程组的解为，其中错误的是（　　）
A．①② B．①③ C．②③ D．①②③
二、填空题
15．（2022春·上海·八年级校考期中）已知正比例函数的图象经过一、三象限，且经过点，则______．
16．（2022秋·上海奉贤·八年级校考期末）当时，不论k取任何实数，函数的值为3，所以直线一定经过定点；同样，直线一定经过的定点为__________．
17．（2022春·湖南长沙·九年级阶段练习）直线与的交点在y轴上，则不等式组的解集为___________．

18．（2022春·陕西咸阳·八年级校考阶段练习）如图，在平面直角坐标系中，直线与直线相交于点，若点的横坐标为1，则关于的二元一次方程组的解是____________．

三、解答题
19．（2022春·重庆合川·八年级期末）“颗粒归仓，饭碗更牢”．夏收是农业四季里的关键一环，冬小麦是夏收的主体粮食，每年的五、六月份是我国冬小麦的收割时间．红星农业合作社租用小型收割机和中型收割机参与冬小麦收割．已知每台中型收割机每小时比每台小型收割机多收割2亩小麦．收割完10亩小麦，每台中型收割机所用时间为每台小型收割机所用时间的．
(1)求每台小型、中型收割机每小时分别收割多少亩小麦；
(2)合作社已租用3台小型收割机和2台中型收割机．由于天气变化，为加快收割进度，合作社决定再租用4台两种型号的收割机．每台小型、中型收割机工作一小时的费用分别为400元、800元，若要使每天收割的小麦不少于480亩，求应再租用几台小型收割机使得每天的费用最少（两种型号收割机每天的工作时长均为6小时）？




20．（2022春·江苏无锡·八年级江苏省天一中学阶段练习）某市规定了每月用水18立方米以内（含18立方米）和用水18立方米以上两种不同的收费标准．该市的用户每月应交水费y（元）是用水量x（立方米）的函数，其图象如图所示．

(1)求当时，y关于x的函数表达式；
(2)若小敏家某月交水费81元，则这个月用水量为_______立方米．
21．（2022春·吉林长春·九年级吉林大学附属中学期末）A、B两地之间有一条高速公路．甲、乙两车分别从A、B两地同时出发，沿此公路相向而行，甲车匀速行驶一段路程后与乙车相遇，相遇后改变了速度继续匀速行驶一段时间到达B地；乙车匀速行驶至A地．两车距A地的路程y（千米）与各自的行驶时间x（时）之间的函数图象如图所示．

(1)乙车的行驶速度为______，两车相遇后甲车的行驶速度为______．
(2)求两车相遇后，甲车距A地的路程y与x之间的函数关系式；
(3)当乙车到达A地时，求甲车距A地的路程（结果保留整数）．





22．（2022春·陕西西安·八年级西安市第二十六中学阶段练习）如图，在平面直角坐标系中，过点的直线与直线相交于点．

(1)请用待定系数法求出直线的函数表达式；
(2)求的面积．





B能力提升
23．（2022秋·北京顺义·八年级阶段练习）如图，在平面直角坐标系中，过点的直线与直线：相交于点．

(1)求直线的表达式；
(2)若直线与y轴交于点C，过动点且平行于的直线与线段AC有交点，求的取值范围．




24．（2022春·山东青岛·九年级青岛三十九中期末）阅读材料
通过前面的学习我们已经知道了两点之间的距离，点到直线的距离和两条平行线间的距离，那么我们如何在平面直角坐标系中求这些距离呢？
如图，在平面直角坐标系中，A、B两点的坐标分为，，由勾股定理得，所以A、B两点间的距离为．这样就可以求出平面直角坐标系中任意两点间的距离.我们用下面的公式可以求出平面直角坐标系中任意一点到某条直线的距离：
已知点和直线，则点P到直线的距离d可用公式．

计算：例如：求点到直线的距离．
解：因为直线可变形为，其中，．
所以点到直线的距离了为．
根据以上材料，解决下列问题：
(1)已知，，求线段AB的长度；
(2)点到直线的距离，并说明点P与直线的位置关系；
(3)点到直线的距离；
(4)已知直线与平行，求这两条直线的距离．







25．（2022春·重庆北碚·七年级统考期末）永辉超市要购进A、B两种型号的电压力锅，已知购进2台A和3台B花费1650元；购进1台A和2台B花费1000元．
(1)求A和B两种型号的压力锅每台进价分别是多少元．
(2)为了满足市场需求，超市决定用不超过19150元采购A、B两种型号的压力锅共60台，且B型号压力锅的数量的2倍不低于A型号压力锅，该商场有几种进货方式．
(3)在（2）的条件下A型号压力锅促销期间售价是389元，B型号压力锅促销期间售价是469元，该超市选择哪种进货方式利润最大．

答案与解析
A基础训练
一、单选题
1．（2022春·陕西宝鸡·八年级统考期中）将直线向右平移2个单位后，所得直线解析式为（　　）
A． B． C． D．
【答案】C
【详解】解：将直线向右平移2个单位长度得到的直线解析式为：
，即．
故选：C．
2．（2022春·全国·八年级专题练习）一次函数的图象如图所示，则关于x的方程的解为（　　）

A． B． C． D．
【答案】B
【详解】解：∵直线与x轴交点坐标为，
∴的解为，
故选：B．
3．（2022春·全国·八年级专题练习）一次是常数的图象如图所示，则关于x的方程的是（　　）

A．x＝3 B．x＝4 C．x＝0 D．x＝b
【答案】A
【详解】由图象知，一次函数的图象过点（3，4），
所以有，
所以是方程的解，
故选：A．
4．（2022春·全国·八年级专题练习）如图，两个一次函数图像的交点坐标为，则关于，的方程组的解为（　　）

A． B． C． D．
【答案】A
【详解】解：方程组的解就是两个函数的交点坐标，即，
故选：A．
5．（2022春·安徽宿州·八年级期末）如图，关于x，y的方程组的解是（      ）

A． B． C． D．
【答案】D
【详解】解：由函数图象可得：直线与直线的交点坐标为：，
即方程组的解为，
∴关于x，y的方程组的解是．
故选：D．
6．（2022春·江苏苏州·八年级校考阶段练习）已知点，在一次函数的图象上，且，则的取值范围是（    ）
A． B． C． D．
【答案】A
【详解】解：∵点，在一次函数的图象上，
此时，，
∴y随x的增大而减小，
∴，解得，
故选：A．
7．（2022春·重庆沙坪坝·八年级重庆八中校考期中）将一次函数与的图像画在同一坐标系中，正确的是（　　）
A． B．
C． D．
【答案】C
【详解】解：一次函数的与一次函数的矛盾，错误；
从图像知，一次函数的图像不经过原点，错误；
一次函数的与一次函数的一致，正确；
从图像知，一次函数的图像不经过原点，错误．
故选：．
8．（2022春·江苏无锡·八年级江苏省天一中学阶段练习）点A()和B()都在直线上，则和的大小关系是（  　）
A． B． C． D．无法确定
【答案】A
【详解】解：∵直线的，
∴y随x的增大而减小，
∵，
∴，
故选：A．
9．（2022春·八年级单元测试）对于函数，下列结论正确的是（    ）
A．它的图象必经过点 B．它的图象经过第一、二、三象限
C．当时， D．的值随值的增大而增大
【答案】C
【详解】解：A．当时，，它的图象不经过点，故A错误；
B．，，它的图象经过第一、二、四象限，故B错误；
C．当时，，当时，，故C正确；
D．，的值随值的增大而减小，故D错误．
故选：C．
10．（2022春·广东深圳·八年级统考期末）己知一次函数，y随着x的增大而减小，则在直角坐标系内它的大致图象是（  ）
A． B．
C． D．
【答案】A
【详解】解：由题意可得，
∵y随着x的增大而减小，
∴必过二四象限，
∵，
∴函数图像过一、二、四象限，
故选A．
11．（2022春·陕西西安·八年级校考期中）一次函数与的图象在同一坐标系中可能是（　　）
A． B．
C． D．
【答案】D
【详解】解：A、由的图象可知，，；由的图象可知，，，即，两结论矛盾，故不符合题意；
B、由的图象可知，，；由的图象可知，，，即，两结论矛盾，故不符合题意；
C、由的图象可知，，；由的图象可知，，，即，两结论相矛盾，故不符合题意；
D、由的图象可知，，；由的图象可知，，，即，两结论符合，故符合题意．
故选：D．
12．（2022春·重庆万州·九年级重庆市万州第二高级中学期末）网语期印，李明同学在老家学习生活，为缓解线上学习疲劳，在某个周末和爸爸进行登山锻炼，登山过程中，两人距地面的高度y(米)与登山时间x(分钟)之间的函数图像如图所示(甲为爸爸，乙为李明)，李明提速后，李明的登山速度是原来速度的2倍，并先到达山顶.根据图象所提供的信息，下列说法情误的是（  ）

A．甲登山的速度是每分钟米
B．乙在A地时距地面的高度b为米
C．乙登山分钟时追上甲
D．登山时间为5分钟、8分钟、分钟时，甲、乙两人距地面的高度差为米
【答案】C
【详解】解：由题意可得，，故A正确；
设 段解析式为，将代入即可得到，，
∴，将代入即可得到：，故B正确；
由上述可得甲的速度为，乙的速度为，
∵李明提速后，李明的登山速度是原来速度的2倍，
∴李明后来的登山速度是，
结合图像及路程=速度时间可得，
甲的解析式为：，乙的解析式为：，
当乙追上甲时有：，
解得：，故C错误；
当时，；
当时，；
当时，；故D正确；
故选C．
13．（2022春·浙江杭州·九年级萧山区党湾镇初级中学校考期中）将二次函数的图象向右平移1个单位，再向上平移2个单位后，顶点在直线上，则k的值为（    ）
A．2 B．1 C．0 D．
【答案】C
【详解】解：∵二次函数的顶点坐标为，
∴将的图象向右平移1个单位，向上平移2个单位后顶点坐标为．
根据顶点在直线上，得，
解得．
故选C．
14．（2022春·全国·八年级专题练习）已知直线与直线交于点P，且点P的横坐标为3，下列结论：
①关于x的方程的解为；
②对于直线，当时，；
③方程组的解为，其中错误的是（　　）
A．①② B．①③ C．②③ D．①②③
【答案】B
【详解】解：直线与直线交于点P，且点P的横坐标为3，
将P点横坐标代入直线，
得，
∴，
将点P坐标代入直线，
得，
解得，
∴，
当时，，
故①选项符合题意；
当时，，
故②选项不符合题意；
∵直线与直线交于点，
∴联立与的解为，
方程组的解为，
故③选项符合题意，
综上，错误的选项有：①③，
故选：B．
二、填空题
15．（2022春·上海·八年级校考期中）已知正比例函数的图象经过一、三象限，且经过点，则______．
【答案】1
【详解】解：∵正比例函数的图象经过一、三象限，
∴．
把代入，得
，
解得或（舍去）．
故答案为：1．
16．（2022秋·上海奉贤·八年级校考期末）当时，不论k取任何实数，函数的值为3，所以直线一定经过定点；同样，直线一定经过的定点为__________．
【答案】
【详解】解：根据题意，可化为，
∴当时，不论取何实数，函数的值为，
∴直线一定经过的定点为，
故答案为．
17．（2022春·湖南长沙·九年级阶段练习）直线与的交点在y轴上，则不等式组的解集为___________．

【答案】
【详解】解：对于直线，
当时，，当时，，
∴直线与y轴的交点为，与x轴的交点为，
观察图象得：当时，直线位于x轴的下方，此时，
当时，，
∴不等式组的解集为．
故答案为：．
18．（2022春·陕西咸阳·八年级校考阶段练习）如图，在平面直角坐标系中，直线与直线相交于点，若点的横坐标为1，则关于的二元一次方程组的解是____________．

【答案】
【详解】解：将代入中，
得，
∴点的坐标为，
∵直线与直线相交于点，
∴方程组组的解为．

三、解答题
19．（2022春·重庆合川·八年级期末）“颗粒归仓，饭碗更牢”．夏收是农业四季里的关键一环，冬小麦是夏收的主体粮食，每年的五、六月份是我国冬小麦的收割时间．红星农业合作社租用小型收割机和中型收割机参与冬小麦收割．已知每台中型收割机每小时比每台小型收割机多收割2亩小麦．收割完10亩小麦，每台中型收割机所用时间为每台小型收割机所用时间的．
(1)求每台小型、中型收割机每小时分别收割多少亩小麦；
(2)合作社已租用3台小型收割机和2台中型收割机．由于天气变化，为加快收割进度，合作社决定再租用4台两种型号的收割机．每台小型、中型收割机工作一小时的费用分别为400元、800元，若要使每天收割的小麦不少于480亩，求应再租用几台小型收割机使得每天的费用最少（两种型号收割机每天的工作时长均为6小时）？
【答案】(1)每台小型收割机每小时收割8亩，则每台中型收割机每小时收割10亩
(2)应再租用2台小型收割机使得每天的费用最少
【详解】（1）设每台小型收割机每小时收割x亩，则每台中型收割机每小时收割亩，
根据题意列方程得，，
解得，
经检验，是原方程的解，
∴
答：每台小型收割机每小时收割8亩，则每台中型收割机每小时收割10亩；
（2）设再租用m台小型收割机，则再租用台中型收割机，
根据题意得，，
解得，
设每天的总费用为w，则，
∵，
∴w随m的增大而减小，
∴小型收割机越多，费用越少，
∴应再租用2台小型收割机使得每天的费用最少．
20．（2022春·江苏无锡·八年级江苏省天一中学阶段练习）某市规定了每月用水18立方米以内（含18立方米）和用水18立方米以上两种不同的收费标准．该市的用户每月应交水费y（元）是用水量x（立方米）的函数，其图象如图所示．

(1)求当时，y关于x的函数表达式；
(2)若小敏家某月交水费81元，则这个月用水量为_______立方米．
【答案】(1)（x＞18）
(2)30
【详解】（1）设函数解析式为 ，
∵直线经过点，，
∴，
解得，
∴函数的解析式为；
（2）由，得用水量超过18立方米，当，，
解得．
所以这个月用水量为30立方米．
故答案为：30．
21．（2022春·吉林长春·九年级吉林大学附属中学期末）A、B两地之间有一条高速公路．甲、乙两车分别从A、B两地同时出发，沿此公路相向而行，甲车匀速行驶一段路程后与乙车相遇，相遇后改变了速度继续匀速行驶一段时间到达B地；乙车匀速行驶至A地．两车距A地的路程y（千米）与各自的行驶时间x（时）之间的函数图象如图所示．

(1)乙车的行驶速度为______，两车相遇后甲车的行驶速度为______．
(2)求两车相遇后，甲车距A地的路程y与x之间的函数关系式；
(3)当乙车到达A地时，求甲车距A地的路程（结果保留整数）．
【答案】(1)，；
(2)
(3)千米
【详解】（1）解：由图象可得：乙车的行驶速度为，
两车相遇后甲车的行驶速度为．
（2）设两车相遇后，甲车距A地的路程y与x之间的函数关系式为，
把，代入解析式可得：
，解得：，
∴函数解析式为：．
（3）乙车到达A地的时间为：（小时），
把代入得：
，
∴乙车到达A地时，甲车距A地的路程约为千米．
22．（2022春·陕西西安·八年级西安市第二十六中学阶段练习）如图，在平面直角坐标系中，过点的直线与直线相交于点．

(1)请用待定系数法求出直线的函数表达式；
(2)求的面积．
【答案】(1)
(2)2
【详解】（1）解：设直线的函数表达式为，
把，代入得：
，
解得：，
∴直线的函数表达式为：．
（2）解：把代入得：，
解得：，
∴点B的坐标为：，
∴．
B能力提升
23．（2022秋·北京顺义·八年级阶段练习）如图，在平面直角坐标系中，过点的直线与直线：相交于点．

(1)求直线的表达式；
(2)若直线与y轴交于点C，过动点且平行于的直线与线段AC有交点，求的取值范围．
【答案】(1)
(2)
【详解】（1）解：依题意，在上，
∴，
∴，
设的表达式为：，
将点，代入得，
，
解得：，
∴的表达式为：；
（2）解：由的表达式为：，令，解得，
∴,
依题意，过动点且平行于的直线为，
∵与线段，有交点，
当过点时，，解得：，
当过点时，，
∴．
24．（2022春·山东青岛·九年级青岛三十九中期末）阅读材料
通过前面的学习我们已经知道了两点之间的距离，点到直线的距离和两条平行线间的距离，那么我们如何在平面直角坐标系中求这些距离呢？
如图，在平面直角坐标系中，A、B两点的坐标分为，，由勾股定理得，所以A、B两点间的距离为．这样就可以求出平面直角坐标系中任意两点间的距离.我们用下面的公式可以求出平面直角坐标系中任意一点到某条直线的距离：
已知点和直线，则点P到直线的距离d可用公式．

计算：例如：求点到直线的距离．
解：因为直线可变形为，其中，．
所以点到直线的距离了为．
根据以上材料，解决下列问题：
(1)已知，，求线段AB的长度；
(2)点到直线的距离，并说明点P与直线的位置关系；
(3)点到直线的距离；
(4)已知直线与平行，求这两条直线的距离．
【答案】(1)
(2)，点P在直线下方
(3)
(4)
【详解】（1）∵，，
∴，
即线段AB的长度为；
（2）∵直线可变形为，其中，．
∵，
∴，
令，，
∵，
∴点P在直线下方；
（3）∵直线可变形为，其中，．
∵，
∴；
（4）令，，
∴点在直线上，
∵直线可变形为，其中，．
∴点到直线的距离为：，
∴直线与的距离为．
25．（2022春·重庆北碚·七年级统考期末）永辉超市要购进A、B两种型号的电压力锅，已知购进2台A和3台B花费1650元；购进1台A和2台B花费1000元．
(1)求A和B两种型号的压力锅每台进价分别是多少元．
(2)为了满足市场需求，超市决定用不超过19150元采购A、B两种型号的压力锅共60台，且B型号压力锅的数量的2倍不低于A型号压力锅，该商场有几种进货方式．
(3)在（2）的条件下A型号压力锅促销期间售价是389元，B型号压力锅促销期间售价是469元，该超市选择哪种进货方式利润最大．
【答案】(1)A型号压力锅的进价为300元/台，B型号压力锅的进价为350元/台
(2)有4种进货方式
(3)购进37台A型号压力锅、23台B型号压力锅时，全部销售完后获得的利润最大
【详解】（1）设A型号压力锅的进价为x元/台，B型号压力锅的进价为y元/台，
依题意得：，
解得：．
答：A型号压力锅的进价为300元/台，B型号压力锅的进价为350元/台．
（2）设购进m台B型号压力锅，则购进台A型号压力锅，
依题意得：，
解得：．
又∵m为整数，
∴m可以取20，21，22，23，
∴该商场有4种进货方式．
（3）设该商场将两种压力锅全部售出后获得的利润为w元，
则，
∵，
∴w随m的增大而增大，
∴当时，w取得最大值，此时，
∴该超市购进37台A型号压力锅、23台B型号压力锅时，全部销售完后获得的利润最大．