专题12二次函数与线段和（将军饮马型）最值问题-挑战2023年中考数学压轴题之学霸秘笈大揭秘（学生版）

挑战2023年中考数学压轴题之学霸秘笈大揭秘(全国通用)          专题12二次函数与线段和(将军饮马型)最值问题   二次函数与将军饮马问题必备的基础模型有：模型1：当两定点A、B在直线l同侧时，在直线l上找一点P，使得PA＋PB最小．        作点B关于直线l的对称点B'，连接AB'交直线l于点P，点P即为所求作的点．PA＋PB的最小值为AB'模型2：当两定点A、B在直线l同侧时，在直线l上找一点P，使得最大．  连接AB并延长交直线l于点P，点P即为所求作的点，的最大值为AB模型3：当两定点A、B在直线l异侧时，在直线l上找一点P，使得最大． 作点B关于直线I的对称点B'，连接AB'并延长交直线l于点P，点P即为所求作的点．的最大值为AB'模型4：点P在∠AOB内部，在OB边上找点D，OA边上找点C，使得△PCD周长最小．  分别作点P关于OA、OB的对称点P′、P″，连接P′P″，交OA、OB于点C、D，点C、D即为所求．△PCD周长的最小值为P′P″模型5：点P在∠AOB内部，在OB边上找点D，OA边上找点C，使得PD＋CD最小．        作点P关于OB的对称点P′，过P′作P′C⊥OA交OB，PD＋CD的最小值为P′C
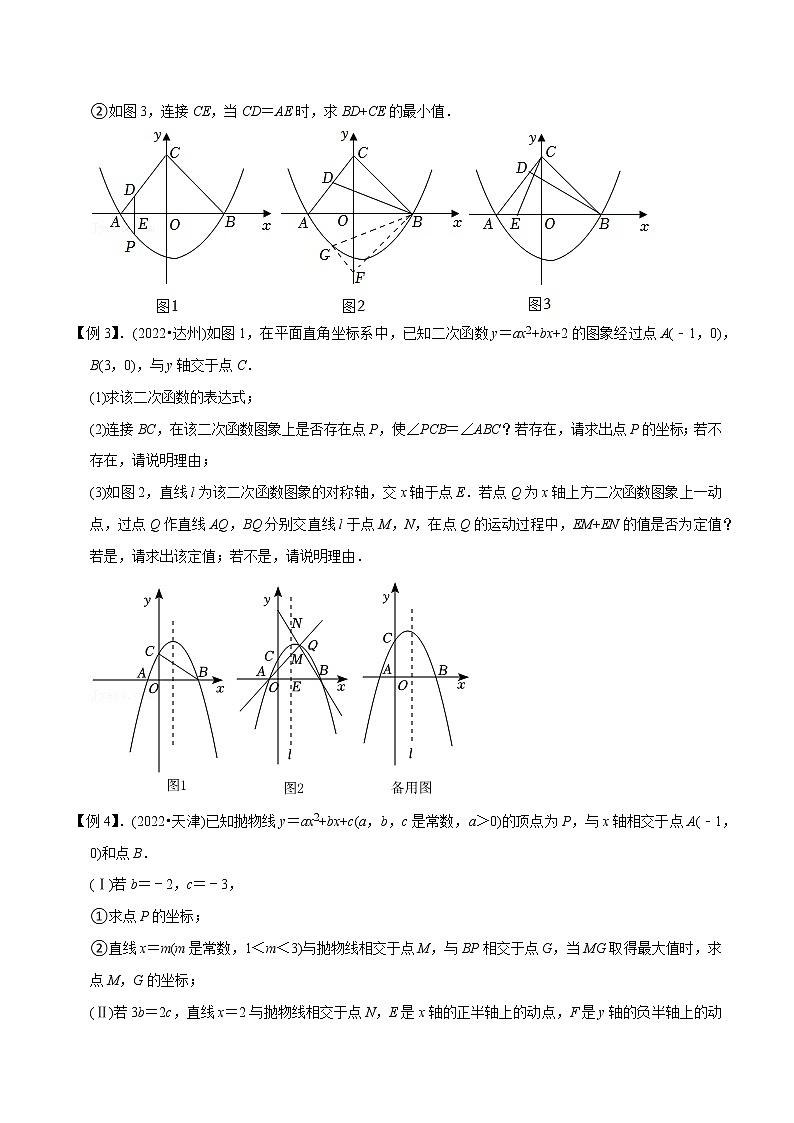
【例1】(2022•黑龙江)如图，已知抛物线y＝(x﹣2)(x+a)(a＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．(1)若抛物线过点M(﹣2，﹣2)，求实数a的值；(2)在(1)的条件下，解答下列问题；①求出△BCE的面积；②在抛物线的对称轴上找一点H，使CH+EH的值最小，直接写出点H的坐标．【例2】(2022•甘肃)如图1，在平面直角坐标系中，抛物线y＝(x+3)(x﹣a)与x轴交于A，B(4，0)两点，点C在y轴上，且OC＝OB，D，E分别是线段AC，AB上的动点(点D，E不与点A，B，C重合)．(1)求此抛物线的表达式；(2)连接DE并延长交抛物线于点P，当DE⊥x轴，且AE＝1时，求DP的长；(3)连接BD．①如图2，将△BCD沿x轴翻折得到△BFG，当点G在抛物线上时，求点G的坐标；②如图3，连接CE，当CD＝AE时，求BD+CE的最小值．【例3】．(2022•达州)如图1，在平面直角坐标系中，已知二次函数y＝ax2+bx+2的图象经过点A(﹣1，0)，B(3，0)，与y轴交于点C．(1)求该二次函数的表达式；(2)连接BC，在该二次函数图象上是否存在点P，使∠PCB＝∠ABC？若存在，请求出点P的坐标；若不存在，请说明理由；(3)如图2，直线l为该二次函数图象的对称轴，交x轴于点E．若点Q为x轴上方二次函数图象上一动点，过点Q作直线AQ，BQ分别交直线l于点M，N，在点Q的运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由．【例4】．(2022•天津)已知抛物线y＝ax2+bx+c(a，b，c是常数，a＞0)的顶点为P，与x轴相交于点A(﹣1，0)和点B．(Ⅰ)若b＝﹣2，c＝﹣3，①求点P的坐标；②直线x＝m(m是常数，1＜m＜3)与抛物线相交于点M，与BP相交于点G，当MG取得最大值时，求点M，G的坐标；(Ⅱ)若3b＝2c，直线x＝2与抛物线相交于点N，E是x轴的正半轴上的动点，F是y轴的负半轴上的动点，当PF+FE+EN的最小值为5时，求点E，F的坐标．【例5】(2022•常德)如图，已知抛物线过点O(0，0)，A(5，5)，且它的对称轴为x＝2，点B是抛物线对称轴上的一点，且点B在第一象限．(1)求此抛物线的解析式；(2)当△OAB的面积为15时，求B的坐标；(3)在(2)的条件下，P是抛物线上的动点，当PA﹣PB的值最大时，求P的坐标以及PA﹣PB的最大值．1．(2022•滨城区二模)如图，抛物线y＝ax2+bx+3(a≠0)，经过点A(﹣1，0)，B(3，0)两点．(1)求抛物线的解析式及顶点M的坐标；(2)连接AC、BC，N为抛物线上的点且在第四象限，当S△NBC＝S△ABC时，求N点的坐标；(3)在(2)问的条件下，过点C作直线l∥x轴，动点P(m，3)在直线l上，动点Q(m，0)在x轴上，连接PM、PQ、NQ，当m为何值时，PM+PQ+QN最小，并求出PM+PQ+QN的最小值． 2．(2022•淮北模拟)已知抛物线l1：y＝ax2+bx﹣2和直线l2：y＝﹣x﹣均与x轴相交于点A，抛物线l1与x轴的另一个交点为点B(3，0)．(1)求a，b的值；(2)将抛物线l1向右平移h个单位长度，使其顶点C落在直线l2上，求h的值；(3)设抛物线l1和直线l2的另一个交点为点D，点P为抛物线上一个动点，且点P在线段AD的下方(点P不与点A，D重合)，过点P分别作x轴和y轴的平行线，交直线l2于点M，N，记W＝PM+PN，求W的最大值．3．(2022•南宁一模)如图1所示抛物线与x轴交于O，A两点，OA＝6，其顶点与x轴的距离是6．(1)求抛物线的解析式；(2)点P在抛物线上，过点P的直线y＝x+m与抛物线的对称轴交于点Q．①当△POQ与△PAQ的面积之比为1：3时，求m的值；②如图2，当点P在x轴下方的抛物线上时，过点B(3，3)的直线AB与直线PQ交于点C，求PC+CQ的最大值．4．(2022•成都模拟)如图，在平面直角坐标系xOy中，二次函数y＝ax2+bx+c(a≠0)的图象与y轴，x轴分别相交于A(0，2)，B(2，0)，C(4，0)三点，点D是二次函数图象的顶点．(1)求二次函数的表达式；(2)点P为抛物线上异于点B的一点，连接AC，若S△ACP＝S△ACB，求点P的坐标；(3)M是第四象限内一动点，且∠AMB＝45°，连接MD，MC，求2MD+MC的最小值．5．(2022•成都模拟)如图1，在平面直角坐标系xOy中，抛物线y＝a(x﹣1)(x+3)的图象与x轴交于点A，B(A在B的左边)，且经过点C(﹣2，3)，P为抛物线的顶点．(1)求抛物线的解析式及点P的坐标；(2)平面内一动点H自点C出发，先到达x轴上的某点M，再到达y轴上某点N，最后运动到点P，求使点H运动的总路径最短的点M，点N的坐标，并求出这个最短总路径的长；(3)如图2，过点C的直线l与抛物线有唯一的公共点，将直线l向下平移交抛物线于D，E两点，连BD交y轴正半轴于F，连BE交y轴负半轴于G，试判断|OF﹣OG|是否为定值，若是，求出该定值；若不是，请说明理由．6．(2022•沈阳模拟)定义：在平面直角坐标系中，抛物线y＝ax2+bx+c的“衍生直线”为y＝﹣ax+b，有一个顶点在抛物线上，另一个顶点在“衍生直线”上的三角形为该抛物线的“衍生三角形”．如图1，已知抛物线y＝﹣x2+2x+3与其“衍生直线”交于A，D两点(点A在点D的左侧)，与x轴正半轴相交于点B，与y轴正半轴相交于点C，点P为抛物线的顶点．(1)填空：该抛物线的“衍生直线”的解析式为 　   　；B的坐标为 　   　；D的坐标为 　   　．(2)如图1，动点E在线段AB上，连接DE，DB，将△BDE以DE所在直线为对称轴翻折，点B的对称点为F，若三角形△DEF为该抛物线的“衍生三角形”，且F不在抛物线上，求点F坐标．(3)抛物线的“衍生直线”上存在两点M，N(点M在点N的上方)，且MN＝，连接PM，CN，当PM+MN+CN最短时，请直接写出此时点N的坐标．7．(2022•沈阳模拟)如图，抛物线y＝ax2+bx+(a≠0)经过点A(3，2)和点B(4，﹣)，且与y轴交于点C．(1)分别求抛物线和直线BC的解析式；(2)在x轴上有一动点G，抛物线上有一动点H，是否存在以O，A，G，H为顶点的四边形是平行四边形？若存在，求出点H的坐标；若不存在，请说明理由；(3)点D为抛物线上位于直线BC上方的一点，过点D作DE⊥x轴交直线BC于点E，点P为对称轴上一动点，当线段DE的长度最大时，求PD+PA的最小值．8．(2022•沈河区二模)如图，在平面直角坐标系中，抛物线y＝ax2+x+c(a≠0)与x轴交于点A(﹣1，0)和B(点B在A的右侧)，与y轴交于点C(0，2)，点P是抛物线上的一个动点．(1)求抛物线的解析式；(2)连接AP，与y轴交于点D，连接BD，当△BOD≌△COA时，求点P的坐标；(3)连接OP，与线段BC交于点E，点Q是x轴正半轴上一点，且CE＝BQ，当OE+CQ的值最小时，请直接写出点Q的坐标． 9．(2022•邵阳县模拟)如图，直线l：y＝﹣3x﹣6与x轴、y轴分别相交于点A、C；经过点A、C的抛物线C：与x轴的另一个交点为点B，其顶点为点D，对称轴与x轴相交于点E．(1)求抛物线C的对称轴．(2)将直线l向右平移得到直线l1．①如图①，直线l1与抛物线C的对称轴DE相交于点P，要使PB+PC的值最小，求直线l1的解析式．②如图 ②，直线l1与直线BC相交于点F，直线l1上是否存在点M，使得以点A、C、F、M为顶点的四边形是菱形，若存在，求出点M的坐标；若不存在，请说明理由． 10．(2021•越秀区校级二模)在平面直角坐标系中，直线y＝﹣x+2与x轴交于点B，与y轴交于点C，抛物线y＝﹣x2+bx+c的对称轴是直线x＝与x轴的交点为点A，且经过点B、C两点．(1)求抛物线的解析式；(2)点M为抛物线对称轴上一动点，当|BM﹣CM|的值最小时，求出点M的坐标；(3)抛物线上是否存在点N，过点N作NH⊥x轴于点H，使得以点B、N、H为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．11．(2022•立山区一模)已知点A(﹣2，0)，B(3，0)，抛物线y＝ax2+bx+4过A，B两点，交y轴于点C．(1)求抛物线的解析式；(2)点P是线段AC上一动点(不与C点重合)，作PQ⊥BC交抛物线于点Q，PH⊥x轴于点H．①连结CQ，BQ，PB，当四边形PCQB的面积为时，求P点的坐标；②直接写出PH+PQ的取值范围．12．(2021•招远市一模)如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A(﹣1，0)，C(2，3)两点，与y轴交于点N．其顶点为D．(1)抛物线及直线AC的函数关系式；(2)若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；(3)若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．(4)设点M的坐标为(3，m)，直接写出使MN+MD的和最小时m的值．13．(2021•桓台县二模)在平面直角坐标系中，抛物线y＝x2+bx+c交x轴于A，B两点，点A，B的坐标分别为(﹣1，0)，(3，0)，点M为顶点．(1)求抛物线的解析式；(2)过点M作y轴的垂线，垂足为C，过点B作y轴的平行线，交CM于点D，点H为OC上的任一点，将线段HB绕点H逆时针旋转90°到HP．求∠PCD的度数；(3)在(2)的条件下，将点H改为y轴上的一动点，连接OP，BP，求OP+BP的最小值．14．(2021•成都模拟)如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+c与x轴交于A(﹣1，0)，B(3，0)两点，与y轴交于点C．(1)求抛物线的解析式．(2)点D为第一象限内抛物线上的一动点，作DE⊥x轴于点E，交BC于点F，过点F作BC的垂线与抛物线的对称轴和y轴分别交于点G，H，设点D的横坐标为m．①求DF+HF的最大值；②连接EG，若∠GEH＝45°，求m的值．15．(2020•朝阳)如图，抛物线y＝﹣+bx+c与x轴交于点A，点B，与y轴交于点C，抛物线的对称轴为直线x＝﹣1，点C坐标为(0，4)．(1)求抛物线表达式；(2)在抛物线上是否存在点P，使∠ABP＝∠BCO，如果存在，求出点P坐标；如果不存在，请说明理由；(3)在(2)的条件下，若点P在x轴上方，点M是直线BP上方抛物线上的一个动点，求点M到直线BP的最大距离；(4)点G是线段AC上的动点，点H是线段BC上的动点，点Q是线段AB上的动点，三个动点都不与点A，B，C重合，连接GH，GQ，HQ，得到△GHQ，直接写出△GHQ周长的最小值．16．(2021•大庆)如图，抛物线y＝ax2+bx+c与x轴交于原点O和点A，且其顶点B关于x轴的对称点坐标为(2，1)．(1)求抛物线的函数表达式；(2)抛物线的对称轴上存在定点F，使得抛物线y＝ax2+bx+c上的任意一点G到定点F的距离与点G到直线y＝﹣2的距离总相等．①证明上述结论并求出点F的坐标；②过点F的直线l与抛物线y＝ax2+bx+c交于M，N两点．证明：当直线l绕点F旋转时，+是定值，并求出该定值；(3)点C(3，m)是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQBC周长最小，直接写出P，Q的坐标．17．(2020•滨州)如图，抛物线的顶点为A(h，﹣1)，与y轴交于点B(0，﹣)，点F(2，1)为其对称轴上的一个定点．(1)求这条抛物线的函数解析式；(2)已知直线l是过点C(0，﹣3)且垂直于y轴的定直线，若抛物线上的任意一点P(m，n)到直线l的距离为d，求证：PF＝d；(3)已知坐标平面内的点D(4，3)，请在抛物线上找一点Q，使△DFQ的周长最小，并求此时△DFQ周长的最小值及点Q的坐标．18．(2018•贺州)如图，在平面直角坐标系中，抛物线y＝ax2+bx+c交x轴于A、B两点(A在B的左侧)，且OA＝3，OB＝1，与y轴交于C(0，3)，抛物线的顶点坐标为D(﹣1，4)．(1)求A、B两点的坐标；(2)求抛物线的解析式；(3)过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合)，PA、PB与直线DE分别交于点F、G，当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．19．(2018•烟台)如图1，抛物线y＝ax2+2x+c与x轴交于A(﹣4，0)，B(1，0)两点，过点B的直线y＝kx+分别与y轴及抛物线交于点C，D．(1)求直线和抛物线的表达式；(2)动点P从点O出发，在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒，当t为何值时，△PDC为直角三角形？请直接写出所有满足条件的t的值；(3)如图2，将直线BD沿y轴向下平移4个单位后，与x轴，y轴分别交于E，F两点，在抛物线的对称轴上是否存在点M，在直线EF上是否存在点N，使DM+MN的值最小？若存在，求出其最小值及点M，N的坐标；若不存在，请说明理由．20．(2018•湘潭)如图，点P为抛物线y＝x2上一动点．(1)若抛物线y＝x2是由抛物线y＝(x+2)2﹣1通过图象平移得到的，请写出平移的过程；(2)若直线l经过y轴上一点N，且平行于x轴，点N的坐标为(0，﹣1)，过点P作PM⊥l于M．①问题探究：如图一，在对称轴上是否存在一定点F，使得PM＝PF恒成立？若存在，求出点F的坐标：若不存在，请说明理由．②问题解决：如图二，若点Q的坐标为(1，5)，求QP+PF的最小值．