人教版八年级下册16.1 二次根式精品ppt课件

第十六章 二次根式

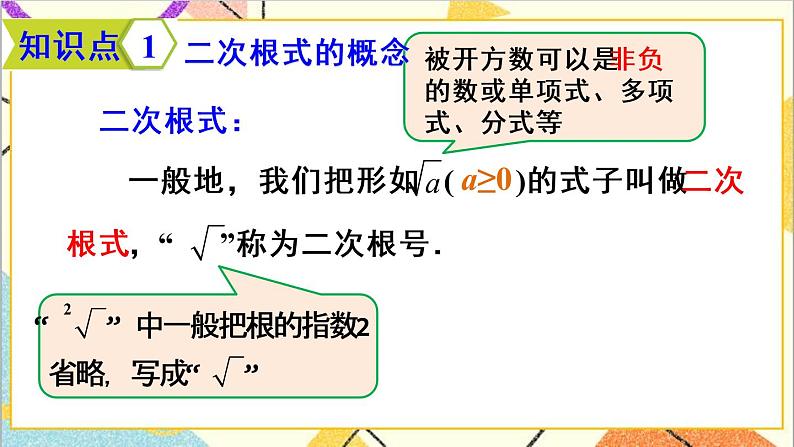
16.1二次根式

第1课时 二次根式的概念

【知识与技能】

了解二次根式的概念，理解是一个非负数.

【过程与方法】通过新旧知识的联系，培养学生观察、演绎能力，发展学生的归纳概括能力.

【情感态度】通过观察一些特殊的情形，获得一般结论，使学生感受归纳的思想方法，进而体验成功的喜悦，并通过合作学习增进终身学习的信念.

【教学重点】二次根式的概念及≥0的基本性质

【教学难点】经历知识产生的过程，探索新知识.

一、情境导入,初步认识

问题   （1）一个长方形的围栏，长是宽的3倍，面积为39m2，则它的宽为_______m；

（2）面积为S的正方形的边长为_______；

（3）一个物体从高处自由落下，落到地面所用的时间t（单位：s）与开始落下的高度h（单位：m）满足关系h=5t2，如果用含h的式子表示t，则t=.______

【教学说明】 设置上述问题的目的是让学生感受到研究二次根式是实际的需要，二次根式与实际生活联系紧密.教师提出问题后，让学生独立思考，然后相互交流，获得对二次根式的感性认识.

二、思考探究，获取新知

思考  通过对上述问题的探究，可得到形如的式子，这些式子有什么特点？

【教学说明】教师提出问题，同学生一道分析，体会这些式子的特征，从而引出二次根式的定义.二次根式：一般地，我们把形如（a≥0）形式的式子称为二次根式，其中“”称为二次根号.针对上述定义，教师可强调以下几点：

（1）中，a必须是大于等于0的数或式子，否则它就没有意义了；

（2）尽管=2，是一个整数，但4仍应称为一个二次根式；

（3）当a≥0时，表示a的算术平方根，而一个非负数的算术平方根必然也是非负数，因而总有≥0（a≥0）

三、典例精析，掌握新知

例1  下列各式中，一定是二次根式的有_______

分析：判断二次根式应关注两点：

（1）有二次根号“”；

（2）被开方数必须是非负数.因而在所给出四个式子中，只有②③中的式子同时符合两个要求，故应填②③.

例2  当x为何值时，下列各式在实数范围内有意义.

解：（1）中，由x-2≥0，得x≥2；

（2）中，由得2≤x≤3；

（3）中，由2x-1＞0，得x＞1/2.

【教学说明】对于例3，教师应引导学生分析题目特征，抓住解决问题的突破口，选择恰当的方法来获得解题思路，进一步体验中a≥0及a≥0的双重非负性特征.

四、运用新知，深化理解

1.填空题：

（1）形如_______的式子叫二次根式；

（2）负数算术平方根________（填“有”或者“没有”）

2.当a是怎样的实数时，下列各式在实数范围内有意义：

【教学说明】学生自主探究，教师巡视，了解学生对本节课知识的掌握情况，及时予以指导，帮助学生巩固新知.

五、师生互动,课堂小结

通过这节课的学习,你掌握了哪些新知识,你获得哪些解决二次根式问题的方法?你还有哪些问题?请与同伴交流.

【教学说明】学生相互交流,回顾知识,反思问题,共同发展提高.

1.布置作业：从教材“习题16.1”中选取.

2.完成练习册中本课时练习.

1.教师创设情境，给出实例.学生积极主动探索，教师引导与启发，师生互动.体现教师的组织者、引导者与合作者地位.

2.注意知识之间的衔接，在温故知新的过程中引导出新知，讲练结合旨在巩固学生对新知的理解.