





初中第二十一章 一次函数21.2 一次函数的图像和性质优秀课件ppt
展开1. 在下列函数是一次函数的是 ,是正比例函数的是_______.2. 函数有哪些表示方法?它们之间有什么关系?探究新知:你能将关系式法转化成图像法吗?什么是函数的图像?
图像法、列表法、关系式法
已知函数的表达式,通过列表、描点和连线,可以在直角坐标系中画出这个函数图像。已知一次函数y =2x-1.(1)填写下表:
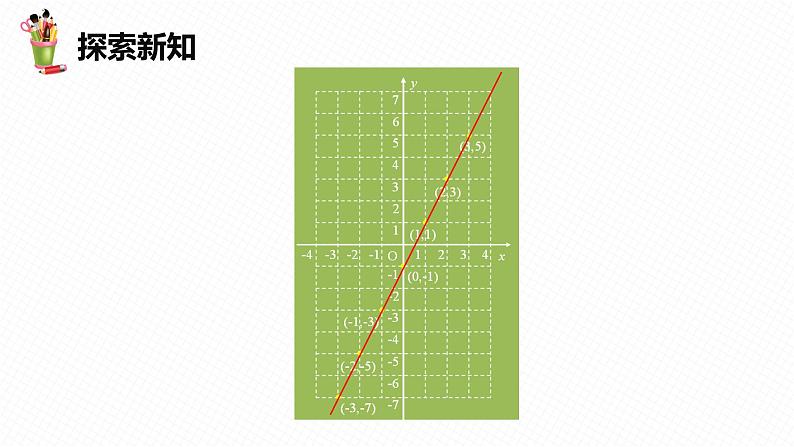
(2)以(1)中得到的每对对应值分别为横坐标和纵坐标,在图中所示的直角坐标系中,描出相应的点.(3)把(2)描出的点依次用平滑曲线连接起来,就得到y =2x-1的图像.(4)一次函数y =2x-1的图像的形状是怎样的?(5)凡是满足关系式y =2x-1的x,y 值所对应的点,如 等,都在一次函数y =2x-1上吗?
一次函数图像的画法与我们前边学过的函数图像的画法一样,其步骤为列表、描点、连线.通过实际操作,我们可得出:(1)一次函数y =kx+b (k、b 为常数,k≠0)的图像是一条直线.由两点确定一条直线可知,在画一次函数图像时,只要描出函数图像中的两个点就可画出此函数的图像.(2)一般地, y=kx+b (k、b 为常数,k≠0)都过(0,b )(与y 轴交点坐标)和( ,0)(与x 轴交点坐标)两点.
例1 画一次函数 的图像.
解: 当x =0时,y =1.当 y=0 时, ,解得x =2.在直角坐标系中,过点(0,1)和点(2,0)画直线,即得一次函数 的图像,如图所示.
画一次函数y=kx+b (k≠0)的图像,通常选取该函数图像与y 轴的交点(横坐标为0的点)和与x 轴的交点(纵坐标为0的点),由两点确定一条直线得一次函数的图像.
1 在同一直角坐标系中,画出y =x 和y =1-x 的图像.
在同一直角坐标系中,画出 和 的图像.
3 在同一直角坐标系中画出y=-3x 和y=3x 的图像.
4 在同一直角坐标系中画出下列函数的图像.(1) y=2x;(2) y=2x +5;(3) y=2x-5
5 一次函数y=x+1的图像是( )A.线段 B.抛物线 C.直线 D.曲线6 函数y=2x+3的图像是( )A.过点(0,3),(0,-1.5)的直线B.过点(0,-1.5),(1,5)的直线C.过点(-1.5,0),(-1,1)的直线D.过点(0,3),(1.5,0)的直线
7 以下四点:(1,2),(2,3),(0,1),(-2,3),在直线y=2x+1上的有( )A.1个 B.2个 C.3个 D.4个8 在平面直角坐标系中,一次函数y=x-1的图像是( )
9 如图,一直线与两坐标轴的正半轴分别交于A,B 两点,P 是线段AB上任意一点(不包括端点),过P 分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为10,则该直线的表达式是( )A.y=x+5 B.y=x+10C.y=-x+5 D.y=-x+10
直线y=kx+b 的位置与系数k,b 的关系
从 k、b 的值看一次函数的图像(1) 当 k>0, b>0时,图像过一、二、三像限;(2) 当 k>0, b<0时,图像过一、三、四像限;(3) 当 k<0, b>0时,图像过一、二、四像限;(4) 当 k<0, b<0时,图像过二、三、四像限.
例2 函数y=x-2的图像不经过( )A.第一象限 B.第二象限C.第三象限 D.第四象限
导引:一次函数y=x-2,∵k=1>0,∴函数图像经过第一、三象限,∵b=-2<0,∴函数图像与y 轴负半轴相交,∴函数图像经过第一、三、四象限,不经过第二象限.故选B.
直线y=kx+b 的位置与k、b 的符号有直接的关系.k>0时,直线必经过第一、三象限;k<0时,直线必经过第二、四象限.b>0时,直线与y 轴正半轴相交;b=0时,直线过原点;b<0时,直线与y 轴负半轴相交.
填表并观察下列两个函数的变化情况.(1)在同一直角坐标系中画出这两个函数的图像.
(2)它们的图像有公共点吗?如果有,请写出公共点的坐标.
它们的图像有公共点.观察图像可得公共点的坐标为(2,-8).
2 今有一根弹簧,不悬挂重物时的长度为12 cm. 悬挂的重物每增加1 kg(重物不超过8 kg).弹簧的长度就增加0.5 cm. 写出弹簧长度:y ( cm)和悬挂物的质量x (kg)之间的函数关系式,指出自变量的取值范围,并画出这个函数的图像.
解: y=12+0.5x (0≤ x ≤8),图像如图所示.
3 在平面直角坐标系中,一次函数y=kx+b 的图像如图所示,观察图像可得( )A.k>0,b>0 B.k>0,b<0C.k<0,b>0 D.k<0,b<0
4 一次函数y=(m-2)x+3的图像如图所示,则m 的取值范围是( )A.m<2 B.0<m<2C.m<0 D.m>2
在平面直角坐标系中,点O 为原点,直线y=kx+b 交x 轴于点A (-2,0),交y 轴于点B.若△AOB 的面积为8,则k 的值为( )A.1 B.-4C.4 D.4或-4
易错点:考虑问题不全面造成漏解.
1 已知等腰三角形的周长是10,底边长y 是腰长x 的函数,则下列图像中,能正确反映y 与x 之间函数关系的图像是( )
2 如图,直线l 经过第一、二、四象限,l 对应的函数表达式是 y=(m-3)x+m+2,则m 的取值范围在数轴上表示为( )
已知y 与x 成正比例,且当x=3时,y=-9. (1)求y 与x 之间的函数关系式; (2)画出函数图像; (3)点P (-1,3)和Q (-6,3)是否在此函数图像上?
(1)设y 与x 之间的函数关系式为y=kx,则-9=3k,解 得k=-3.所以y 与x 之间的函数关系式为y=-3x.(2)列表: 描点,连线,图像如图所示.(3)当x=-1时,y=-3×(-1)=3;当x=-6时,y= -3×(-6)=18≠3,所以点P (-1,3)在此函数图像 上,而点Q (-6,3)不在此函数图像上.
小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中,小敏离家的路程y (米)和所经过的时间x (分)之间的函数图像如图所示.请根据图像回答下列问题:(1)小敏去超市途中的速度是多少?在超市逗留了多长时间?(2)小敏几点几分返回到家中?
(1)小敏去超市途中的速度为 =300(米/分). 在超市逗留了40-10=30(分).(2)设返回途中,y 与x 的函数表达式为y=kx+b (k≠0). 把点(40,3 000),(45,2 000)的坐标代入, 得 解得 ∴返回途中的函数表达式为y=-200x+11 000, 当y=0时,x=55, ∴小敏8:55返回到家中.
在如图所示的平面直角坐标系中,点P 是直线y=x上的动点,点A (1,0),点B (2,0)是x 轴上的两点,求PA+PB 的最小值.
直线y=x 是第一、三象限的角平分线,点A 关于直线y=x 的对称点A′ 的坐标是(0,1),连接A′B 交直线y=x 于点P,此时PA+PB 最小,最小值为
已知一次函数y=2x+4.(1)在如图所示的平面直角坐标系中,画出函数的图像;(2)求图像与x 轴的交点A 的坐标,与y 轴交点B 的坐标;
(3)在(2)的条件下,求出△AOB 的面积;(4)利用图像直接写出当y<0时,x 的取值范围.
(1)当x=0时,y=4,当y=0时,x=-2, 则图像如图所示.(2)由(1)可知点A (-2,0), 点B (0,4).(3)S△AOB= ×2×4=4.(4)由图像得当 y<0时,x<-2.
一般地,一次函数y=kx+b 的图像为一条直线.因此,我们把一次函数y=kx+b 的图像也称为直线y=kx+b. 在画一次函数的图像时,只要确定出两个点,再过这两点画直线就可以了.
一次函数y=kx+b (k、b 为常数,k≠0)的图像与 k、b 的值紧密相连,归纳起来主要有以下几方面.(1) 当 k>0, b>0时,图像过一、二、三像限;(2) 当 k>0, b<0时,图像过一、三、四像限;(3) 当 k<0, b>0时,图像过一、二、四像限;(4) 当 k<0, b<0时,图像过二、三、四像限.
冀教版21.2 一次函数的图像和性质精品课件ppt: 这是一份冀教版21.2 一次函数的图像和性质精品课件ppt,共50页。PPT课件主要包含了课前导入,新课精讲,学以致用,课堂小结,情景导入,探索新知,知识点,一次函数的性质,典题精讲,一次函数性质的应用等内容,欢迎下载使用。
初中数学冀教版八年级下册21.2 一次函数的图像和性质一等奖课件ppt: 这是一份初中数学冀教版八年级下册21.2 一次函数的图像和性质一等奖课件ppt,文件包含河北教育版数学八年级下·212一次函数的图像和性质第2课时一次函数的性质教学课件pptx、212一次函数的图像和性质第2课时教案docx、212一次函数的图像和性质第2课时同步练习docx等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学冀教版八年级下册21.2 一次函数的图像和性质优质课ppt课件: 这是一份初中数学冀教版八年级下册21.2 一次函数的图像和性质优质课ppt课件,文件包含河北教育版数学八年级下·212一次函数的图像和性质第1课时一次函数的图像教学课件pptx、212一次函数的图像和性质第1课时教案docx、212一次函数的图像和性质第1课时同步练习docx等3份课件配套教学资源,其中PPT共17页, 欢迎下载使用。













