初中数学冀教版八年级下册22.4 矩形优秀ppt课件

这是一份初中数学冀教版八年级下册22.4 矩形优秀ppt课件，共53页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，知识回顾，探究新知，探索新知，知识点，由直角的个数判定矩形等内容，欢迎下载使用。
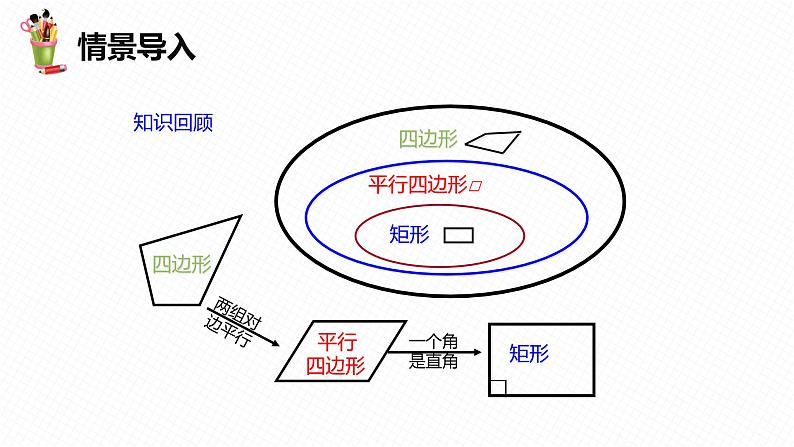
木工朋友在制作窗框后，需要检测所制作的窗框是否是矩形，那么他需要测量哪些数据，其根据又是什么呢？你现在有方法帮他吗？
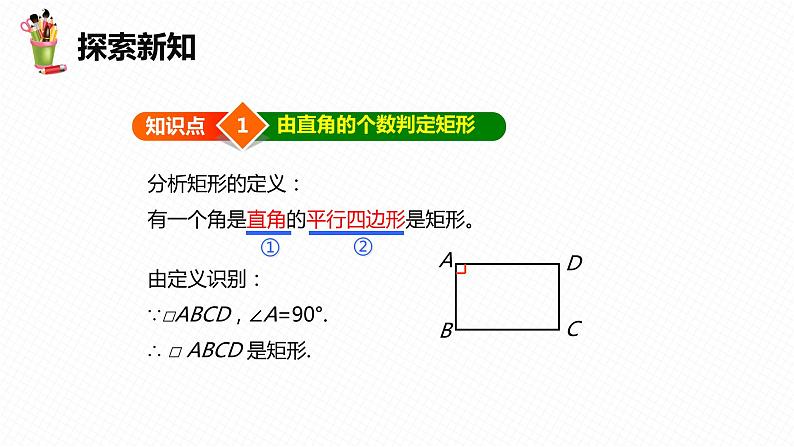
分析矩形的定义：有一个角是直角的平行四边形是矩形。由定义识别：∵□ABCD，∠A=90°.∴ □ ABCD 是矩形.
根据矩形的定义，有一个角是直角的平行四边形是矩形．如果不通过平行四边形，能根据四边形中直角的个数，直接由四边形来判定它是矩形吗？有几个角是直角的四边形是矩形呢？性质：矩形的四个角都是直角四个角是直角的四边形是矩形
李芳同学用“边——直角、边——直角、边——直角、边”这样四步，画出了一个四边形，她说这就是一个矩形。猜想她判断的依据？猜想：有三个角是直角的四边形是矩形 你能证明上述结论吗？已知：如图所示，在四边形ABCD 中，∠A=∠B=∠C=90°. 求证：四边形ABCD 是矩形．
证明：∵ ∠A=∠B=∠C=90°，∴∠A+∠B=180°， ∠B+∠C=180°. ∴AD∥BC，AB∥CD.∴四边形ABCD 是平行四边形. ∵ ∠A=90°， ∴ □ABCD 是矩形.
比较上面两种说法，你认为选择哪种说法作为矩形的判定定理更为简洁?于是，便得到：有三个角是直角的四边形是矩形.
有三个角是直角的四边形是矩形 .符号表达式：∵ ∠A=∠B=∠C=90°， ∴四边形ABCD 是矩形.
例1 如图，▱ABCD 的四个内角的平分线分别相交于 点E，F，G，H.求证：四边形EFGH 是矩形.
要证明四边形EFGH 是矩形，由于已知ABCD 的四个内角的平分线分别相交于点E，F，G，H，因此可选用“有三个角是直角的四边形是矩形”来证明．
∵AB∥CD，∴∠ABC＋∠BCD＝180°.∵BG 平分∠ABC，CG 平分∠BCD，∴∠GBC＋∠GCB＝ ∠ABC＋ ∠BCD ＝ ×180°＝90°，∴∠BGC＝90°. 同理可得∠AFB＝∠AED＝90°.∴∠GFE＝∠FEH＝∠FGH＝90°.∴四边形EFGH 是矩形．
本题目中的图形是建立在四边形基础上，而条件中又涉及角的关系，一般采用“角的方法”来判定矩形．
已知：如图，在△ABC 中，AB=AC，D 为BC 的中点，四边形AEDB 为平行四边形.求证：四边形AECD 是矩形.
在▱AEDB 中，AE＝BD，AE∥BD，AB＝DE，∵D 为BC 的中点，∴BD＝DC，∴AE＝CD，又∵AE∥CD，∴四边形AECD 是平行四边形．在△ABC 中，AB＝AC，∴AC＝DE，∴四边形AECD 是矩形．
已知矩形的对角线长为10 cm，求顺次连接矩形四边中点所得的四边形的周长.
如图所示．在矩形ABCD 中，AC，BD 的长都为10 cm.点E，H 分别是AD，CD 的中点，则EH＝ AC＝5 cm.同理：FE，FG，GH 的长均为5 cm.所以所得到的四边形的周长为5＋5＋5＋5＝20(cm)．
下列命题中，假命题是(　　)A．有一组对角是直角且一组对边平行的四边形是矩形B．有一组对角是直角且一组对边相等的四边形是矩形C．有两个内角是直角且一组对边平行的四边形是矩形D．有两个内角是直角且一组对边相等的四边形是矩形
下列说法：①三角形的三条高一定都在三角形内；②有一个角是直角的四边形是矩形；③两边及一角对应相等的两个三角形全等；④一组对边平行，另一组对边相等的四边形是平行四边形．其中正确的有(　　)A．0个　 　B．1个　　 C．2个 　　D．3个
如图，顺次连接四边形ABCD 各边中点得四边形EFGH，要使四边形EFGH 为矩形，应添加的条件是(　　)A．AB∥DC B．AC＝BD C．AC⊥BD D．AB＝DC
由对角线的关系判定矩形
我们知道，矩形的对角线相等. 反过来，对角线相等的平行四边形是矩形吗？ 工人师傅在做门窗或矩形零件时，不仅要测量两组对边的长度是否分别相等，常常还要测量它们的两条对角线是否相等，以确保图形是矩形.你知道其中的道理吗？
已知：在▱ABCD，AC=BD.求证： ▱ABCD 是矩形.证明：∵ 在▱ABCD 中，AB=DC，BC=CB，且AC=DB.∴ △ABC ≌ △DCB（SSS）.∴ ∠ABC=∠DCB.∵ AB//CD，∴ ∠ABC+∠DCB=180°. ∴ ∠ABC=∠DCB=90°.又∵ 四边形ABCD 是平行四边形，∴ ▱ABCD 是矩形.
可以发现并证明矩形的一个判定定理： 对角线相等的平行四边形是矩形.警示：两条对角线相等的四边形不一定是矩形，这个 四边形必须是平行四边形才可以.
例2 已知：如图，在矩形ABCD 中，E，F，G，H 分别 为OA，OB，OC，OD 的中点. 求证：四边形EFGH 是矩形.
∵四边形ABCD 是矩形，∴AC=BD.且 OA=OC，OB=OD.∴OA=OC=OB=OD.又∵E，F，G，H 分别为OA，OB，OC，OD 的中点，∴OE=OG=OF=OH.∴四边形EFGH 是平行四边形.又∵EG=OE+OG=OF+OH= HF，∴四边形EFGH 是矩形.
证明一个平行四边形为矩形的两种方法：一是证明有一个角是直角，另一个是证明两条对角线相等．
解： (1)(2)(3)错误，(4)正确．
指出下列说法是否正确.(1)有一个角为直角的四边形是矩形.(2)两条对角线相等的四边形是矩形.(3)两条对角线互相垂直的四边形是矩形.(4)四个角皆为直角的四边形是矩形.
如图，矩形ABCD 的两条对角线AC，BD 的夹角为60°，AC+AB= 12.求AC 和AB 的长.
因为两条对角线AC，BD 的夹角为60°，AO＝BO，所以∠OAB＝∠OBA＝∠AOB＝60°，所以△AOB 为等边三角形，AC＝2AB.所以AC＋AB＝2AB＋AB＝3AB＝12.所以AB＝4，所以AC＝8.
小亮想检验一块木板是不是矩形.现仅有一根足够长的细绳，你能想办法帮他进行检验吗？请说明理由.
已知：如图，在△ABC 中，AB=AC，AD⊥BC，垂足为D，AN 是△ABC 外角∠CAM 的平分线，CE⊥AN，垂足为E.求证：四边形ADCE 是矩形.
由题意易知∠MAC＝∠B＋∠ACB，∵AB＝AC，∴∠B＝∠ACB.∴∠MAC＝2∠B，∵AN 是∠MAC 的平分线，∴∠MAC＝2∠MAE，∴∠MAE＝∠B，∴AE∥BC，∵AD⊥BC，∴∠ADB＝∠ADC＝90°，∵CE⊥AN，∴∠AEC＝90°，∵AE∥BC，∴∠DAE＝∠ADB＝90°，∴∠ADC＝∠DAE＝∠AEC＝90°，∴四边形ADCE 是矩形．
如图，在矩形ABCD 中，AC，BD 相交于点O，AE 平分∠BAD，交 BC 于点E，∠CAE= 15°.求∠BOE 的度数.
在矩形ABCD 中，OA＝OB＝OD＝OC，∵AE 平分∠BAD，∴∠BAE＝ ∠BAD＝45°，又∵∠ABE＝90°，∴∠AEB＝45°.∴AB＝BE.∵∠CAE＝15°，∴∠BAO＝60°，∴△AOB 是等边三角形．∴OA＝OB＝AB，∠ABO＝60°，∴BO＝BE，∠OBE＝30°，∴∠BOE＝ ×(180°－30°)＝75°.
如图，在矩形ABCD 中，AB＞BC，点E、F、G、H 分别是边DA、AB、BC、CD 的中点，连接EG、FH，则图中矩形的个数共有(　　)A．5个 B．8个 C．9个 D．11个
如图，四边形ABCD 的对角线互相平分，要使它变为矩形，需要添加的条件是(　　)A．AB＝CD　 B．AD＝BCC．AB＝BC　 D．AC＝BD
下列关于矩形的说法中正确的是(　　)　A．对角线相等的四边形是矩形B．矩形的对角线相等且互相平分C．对角线互相平分的四边形是矩形D．矩形的对角线互相垂直且平分
如图，在▱ABCD 中，延长AD 到点E，使DE＝AD，连接EB，EC，DB，请你添加一个条件_____________________，使四边形DBCE 是矩形．
EB＝DC (答案不唯一)
在一组对边平行的四边形中，添加下列条件中的哪一个，可判定这个四边形是矩形(　　)A．另一组对边相等，对角线相等B．另一组对边相等，对角线互相垂直C．另一组对边平行，对角线相等D．另一组对边平行，对角线互相垂直
易错点：对矩形的判定方法理解错误导致出错
如图，在Rt△ABC 中，∠A＝90°，AB＝3，AC＝4，P 为边BC 上一动点，PE⊥AB 于E，PF⊥AC 于F，则EF 的最小值为(　　)A．2 B．2.2 C．2.4 D．2.5
如图，要使▱ABCD 成为矩形，需添加的条件是(　　)A．AB＝BC B．AO＝BOC．∠1＝∠2 D．AC⊥BD
如图，在平行四边形ABCD 中，点O 是边BC 的中点，连接DO 并延长，交AB 延长线于点E，连接BD，EC.(1)求证：四边形BECD 是平行四边形；
(1)在平行四边形ABCD 中，AB∥CD， ∴∠CBE＝∠BCD， ∵点O 是边BC 的中点，∴OB＝OC， ∵∠BOE＝∠COD， ∴△BOE ≌△COD，∴OE＝OD， ∴四边形BECD 是平行四边形．
(2)若∠A＝50°，则当∠BOD＝________°时，四边形BECD 是矩形．
如图，已知BA＝AE＝DC，AD＝EC，CE⊥AE，垂足为E.(1)求证：△DCA ≌△EAC；(2)只需添加一个条件，即___________，可使四边形ABCD 为矩形．请加以证明．
(1)证明：在△DCA 和△EAC 中， ∴△DCA ≌△EAC (SSS)．(2)解：AD＝BC 证明：∵AB＝DC，AD＝BC， ∴四边形ABCD 是平行四边形． ∵CE⊥AE，∴∠E＝90°. 由(1)得△DCA ≌△EAC， ∴∠D＝∠E＝90°. ∴四边形ABCD 为矩形．
如图，在矩形ABCD 中，AB＝24 cm，BC＝8 cm，点P 从A开始沿折线A→B→C→D 以4 cm/s的速度移动，点Q 从C 开始沿CD 边以2 cm/s的速度移动，如果点P、Q 分别从A、C同时出发，当其中一点到达D 时，另一点也随之停止运动，设运动时间为t s．当t 为何值时，四边形QPBC 为矩形？
根据题意得CQ＝2t cm，AP＝4t cm，则BP＝(24－4t )cm，∵四边形ABCD 是矩形，∴∠B＝∠C＝90°，CD∥AB.∴只有CQ＝BP 时，四边形QPBC 是矩形，即2t＝24－4t.解得t＝4，∴当t＝4时，四边形QPBC 是矩形．
如图，在△ABC 中，点O 是边AC上一个动点，过点O 作直线EF∥BC 分别交∠ACB、外角∠ACD 的平分线于点E、F. (1)若CE＝8，CF＝6，求OC 的长；(2)连接AE、AF.问：当点O 在边AC 上运动到什么位置时，四边形AECF 是矩形？并说明理由．
(1)∵EF 交∠ACB、外角∠ACD 的平分线于点E、F， ∴∠OCE＝∠BCE，∠OCF＝∠DCF. ∵EF∥BC，∴∠OEC＝∠BCE，∠OFC＝∠DCF. ∴∠OEC＝∠OCE，∠OFC＝∠OCF. ∴OE＝OC，OF＝OC. ∴OE＝OF＝ EF. ∵∠OCE＋∠BCE＋∠OCF＋∠DCF＝180°， ∴∠ECF＝90°. 在Rt△CEF 中，由勾股定理得EF＝ ＝10， ∴OC＝OE＝ EF＝5.
(2)当点O 在边AC 上运动到AC 中点时， 四边形AECF 是矩形． 理由如下： 如图所示． 当O 为AC 的中点时，AO＝CO， ∵EO＝FO， ∴四边形AECF 是平行四边形． ∵∠ECF＝90°， ∴平行四边形AECF 是矩形．
方法1：有一个角是直角的平行四边形是矩形.方法2：有三个角是直角的四边形是矩形 .方法3：对角线相等的平行四边形是矩形. (对角线互相平分且相等的四边形是矩形.)