






2023年河北省中考数学复习全方位第8讲 分式方程及其应用 课件
展开解:方程两边同时乘(x+1)·(x-1),得x+1=2(x-1).去括号,得x+1=2x-2.移项并合并同类项,得x=3.经检验,x=3是原方程的解.
2. (2013·河北,7)甲队修路120 m与乙队修路100 m所用天数相同,已知甲队比乙队每天多修10 m,设甲队每天修x m.依题意,下面所列方程正确的是( )
3. (2016·河北,12)在求3x的倒数的值时,嘉淇同学误将3x看成了8x,她求得的值比正确答案小5.依上述情形,所列关系式成立的是( )
1.定义:分母中含有未知数的方程叫做分式方程.2.分式方程的解法(1)基本思路:将分式方程转化为整式方程.(2)解分式方程的步骤:①去分母:方程两边都乘各个分式的① ,约去分母,化成整式方程. ②解这个整式方程.③检验:把求得的未知数的值代入最简公分母中,看是否等于0,使最简公分母为② 的根为原方程的增根,必须舍去.
3.分式方程的增根分式方程的增根是在去分母时产生的,它有两个特点:(1)增根是去分母后所得整式方程的根;(2)增根是使原方程中各分式的最简公分母为0的未知数的值.【易错提示】分式方程的增根与无解并非同一个概念.(1)分式方程的增根是去分母后整式方程的根,也是使分式方程分母为0的根.(2)分式方程无解的原因有两个:一是去分母后的整式方程无解;二是整式方程的解使得最简公分母为0.
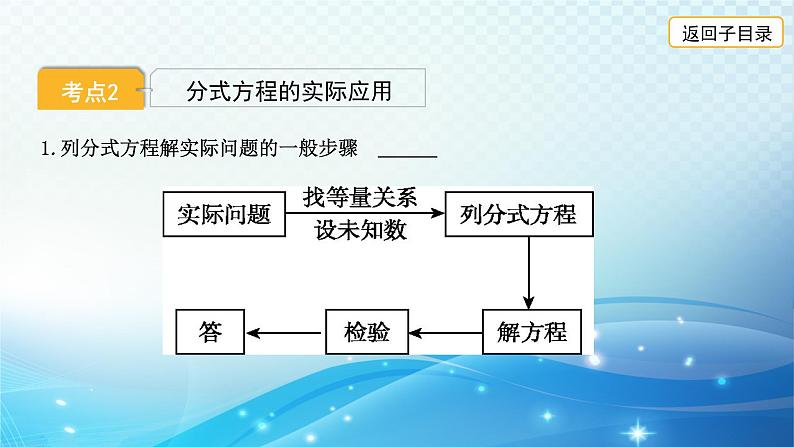
1.列分式方程解实际问题的一般步骤
1.(2021·石家庄模拟)如图,在框中解分式方程的4个步骤中,根据等式基本性质的是( )
A. ①③ B. ①② C. ②④ D. ③④
A. x=2 B. x=-2 C. x=1 D. x=-1
A. a<5 B. a≠3 C. a<5且a≠3 D. a=3
A. 26 B. 32 C. 34 D. 40
解:把方程两边同时乘以(x-2),得x-3+x-2 =-3,解得x=1,检验:当x=1时,x-2 =1-2 =-1≠0,∴原方程的解为x=1.
(2)方程两边同时乘(x-3),得1-x=-1-2x+6,解得x=4.检验:当x=4时,x-3≠0.所以原分式方程的解为x=4.
1. (2021·河北中考模拟)某中学九年级学生去距学校10km的景点参观,一部分学生骑自行车先走,过了30分钟后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑自行车学生速度的2倍.设骑自行车学生的速度为xkm/h,则所列方程正确的是( )
A.实际每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务B.实际每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务C.实际每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务D.实际每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务
3. (2021·石家庄模拟)我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部?
4. (2021·河北模拟)某工厂计划生产一种创新产品,若生产一件这种产品需A种原料1.2千克、B种原料1千克.已知A种原料每千克的价格比B种原料每千克的价格多10元.(1)为使每件产品的成本价不超过34元,那么购入的B种原料每千克的价格最高不超过多少元?(2)将这种产品投放市场批发销售一段时间后,为拓展销路又开展了零售业务,每件产品的零售价比批发价多30元.现用10 000元通过批发价购买该产品的件数与用16 000元通过零售价购买该产品的件数相同,那么这种产品的批发价是多少元?
解:(1)设B种原料每千克的价格为x元,则A种原料每千克的价格为(x+10)元,根据题意,得1.2(x+10)+x≤34,解得x≤10.答:购入的B种原料每千克的价格最高不超过10元.
5. (2021·石家庄模拟)某公司购买了一批A,B型芯片,其中A型芯片的单价比B型芯片的单价少9元,已知该公司用3 120元购买A型芯片的条数与用4 200元购买B型芯片的条数相等.(1)求该公司购买的A,B型芯片的单价各是多少元?(2)若两种芯片共购买了200条,且购买的总费用为6 280元,求购买了多少条A型芯片?
(2)设购买a条A型芯片,则购买(200-a)条B型芯片,依题意可得26a+35(200-a)=6 280,解得a=80.答:购买了80条A型芯片.
6. (2021·唐山模拟)某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30 kg材料,且A型机器人搬运1 000 kg材料所用的时间与B型机器人搬运800 kg材料所用的时间相同.(1)求A,B两种型号的机器人每小时分别搬运多少材料;(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2 800 kg,则至少购进A型机器人多少台?
2023年河北省中考数学复习全方位第13讲 反比例函数及其应用 课件: 这是一份2023年河北省中考数学复习全方位第13讲 反比例函数及其应用 课件,共49页。PPT课件主要包含了真题试做,34≤m≤8,考点梳理,题型突破等内容,欢迎下载使用。
2023年河北省中考数学复习全方位第12讲 一次函数的实际应用 课件: 这是一份2023年河北省中考数学复习全方位第12讲 一次函数的实际应用 课件,共36页。PPT课件主要包含了真题演练,考点梳理,题型突破,4P63等内容,欢迎下载使用。
2023年河北省中考数学复习全方位第9讲 一元二次方程及其应用 课件: 这是一份2023年河北省中考数学复习全方位第9讲 一元二次方程及其应用 课件,共39页。PPT课件主要包含了真题试做,考点梳理,化为1,常数项,分别等于0,题型突破,m≤15等内容,欢迎下载使用。












