2023年河北省中考数学复习全方位第12讲 一次函数的实际应用 课件

这是一份2023年河北省中考数学复习全方位第12讲 一次函数的实际应用 课件，共36页。PPT课件主要包含了真题演练，考点梳理，题型突破，4P63等内容，欢迎下载使用。
命题点 一次函数的实际应用
1. (2019·河北,24)长为300m的春游队伍,以v(m/s)的速度向东行进.如图①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:①求S头与t的函数关系式(不写t的取值范围);②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围);(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
解:(1)①排头走的路程为2t,则S头=2t+300.
②甲从排尾赶到排头时,有4t=2t+300,得t=150.此时,S头=2×150+300=600.甲从排头返回的时间为t-150,则S甲=600-4(t-150)=-4t+1 200.
2. (2015·河北,23)水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.(1)只放入大球,且个数为x大,求y与x大的函数关系式(不必写出x大的范围);(2)仅放入6个大球后,开始放入小球,且小球个数为x小.①求y与x小的函数关系式(不必写出x小的范围);②限定水面高不超过260毫米,最多能放入几个小球?
解:(1)y=210+4x大.
(2)①放入6个大球后水的高度是210+4×6=234(毫米),则y=234+3x小.
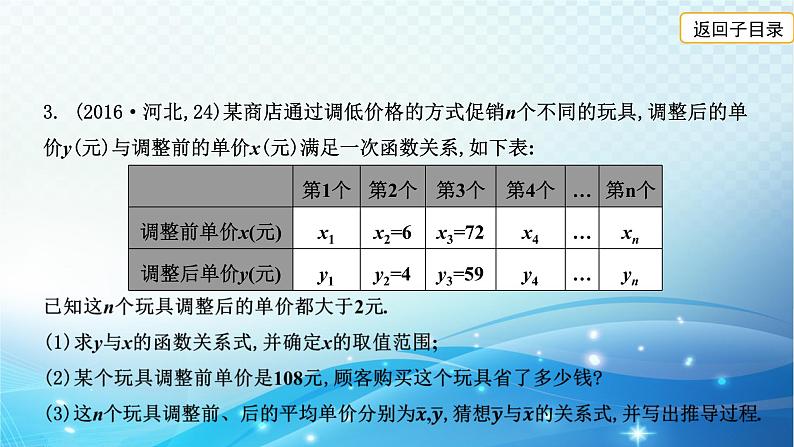
3. (2016·河北,24)某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如下表:
1. 用一次函数解决实际问题的一般步骤(1)设出实际问题中的变量；(2)建立一次函数解析式；(3)利用待定系数法求出一次函数解析式；(4)确定自变量的取值范围；(5)利用一次函数的性质求相应的值,对所求的值进行检验,看其是否符合实际意义；(6)作答.
2. 一次函数实际应用的常考类型(1)根据实际问题中给出的数据列出相应的函数解析式,解决实际问题；(2)利用一次函数对实际问题中的方案进行比较；(3)结合函数图象解决实际问题.
3. 确定解析式常用的等量关系(1)路程问题:路程=速度×时间.(2)利润问题:销售额=单价×销售量,总利润=单件利润×销售量.
【规律总结】一次函数的实际应用一般涉及以下三个问题:(1)求函数解析式.①文字型及表格型的应用题:一般都是根据题干中数量的等量关系来列函数解析式.②图象型的应用题:一般都是找图象上的两个点的坐标,根据待定系数法求函数解析式.
(2)求最优方案.对于最优方案问题,通常涉及两个相关量,解题方法是根据题中所要满足的关系式,通过列不等式,求解出某一个变量的取值范围,再根据另一个变量所要满足的条件,即可确定出有多少种方案.
(3)求最值问题.①可将所有求得的方案的值计算出来,再进行比较;②直接利用所求值与其变量之间满足的一次函数关系式求解,由一次函数的增减性可直接确定最优方案及最值;若为分段函数,则应分类讨论,先计算出每个分段函数的最值,再进行比较.
一次函数与几何图形相结合的主要题型是有关几何图形的面积计算.解题时通常会用到二元一次方程组来求一次函数解析式或交点坐标.
1. (2021·河北联考)甲、乙施工队分别从两端修一段长度为380m的公路,在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.下列说法错误的是(　 　)
A.甲队每天修路20m B.乙队第一天修路15mC.乙队技术改进后每天修路35m D.前七天甲、乙两队修路长度相等
2.(2021·唐山模拟)如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是(　 　)
A.乙前4秒行驶的路程为48米B.在0到8秒内甲的速度每秒增加4米/秒C.两车到第3秒时行驶的路程相同D.在4到8秒内甲的速度都大于乙的速度
3. (2021·保定一模)某旅游风景区门票价格为a元/人,对团体票规定:10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,y与x之间的函数关系如图所示.(1)填空:a=　　　　,b=　　　　. (2)请求出:当x>10时,y与x之间的函数关系式.(3)导游小王带一个旅游团到该景区旅游,付门票费用2 720元(导游不需购买门票),求该旅游团有多少人?
(3)∵2 720>800, ∴将y=2 720代入y=64x+160,得2 720=64x+160,解得x=40,故该旅游团有40人.
4. 如图,购买一种苹果,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省多少元?
5. 一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.(1)求y关于x的函数解析式(不需要写定义域);(2)已知当油箱中的剩余油量为8升时,汽车会开始提示加油.在此行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
6. (2021·石家庄模拟)为了美化环境,建设宜居城市,我市准备在一个广场上种植甲、乙两种花卉.经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.(1)直接写出当0≤x≤300和x>300时,y与x的函数关系式;(2)广场上甲、乙两种花卉的种植面积共1 200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少总费用为多少元?
1. (2021·邯郸模拟)如图,已知一次函数y=2x+a,y=-x+b的图象都经过A(-2,0),且与y轴分别交于B,C两点,则△ABC的面积为(　 　)
A. 4 B. 5 C. 6 D. 7
2. (2021·河北模拟)如图①,在矩形MNPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是(　 　)
A. 当x=2时,y=5B. 矩形MNPQ的周长是18C. 当x=6时,y=10D. 当y=8时,x=10
3. (2021·河北预测)在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为　　　　. 
4. 如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;(2)求直线l2的解析式;(3)求△ADC的面积;(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
解:(1)由y=-3x+3,令y=0,得-3x+3=0,∴x=1,∴D(1,0).
(2)S四边形PCOA=S△ABP-S△OBC=7.
6. (2021·河北模拟)如图,正方形ABCD的边长为2,BC边在x轴上,BC的中点与原点O重合,过定点M(-2,0)与动点P(0,t)的直线MP记做l.(1)若l的解析式为y=2x+4,判断此时点A是否在直线l上,并说明理由;(2)当直线l与AD边有公共点时,求t的取值范围.