2023年河北省中考数学复习全方位第30讲 图形的相似与位似 课件

这是一份2023年河北省中考数学复习全方位第30讲 图形的相似与位似 课件，共36页。PPT课件主要包含了真题演练，AE⊥ED，AEED，考点梳理，比例的性质，相似比，成比例，相似比的平方，对应成比例，位似比等内容，欢迎下载使用。

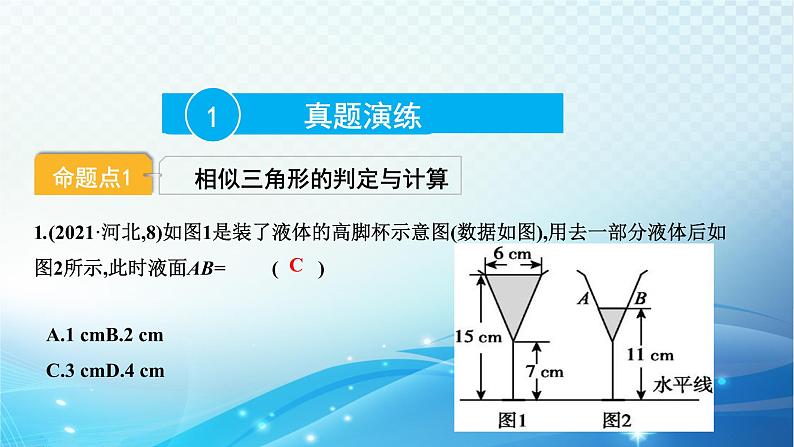
1.(2021·河北,8)如图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB=(　　)
A.1 cmB.2 cmC.3 cmD.4 cm
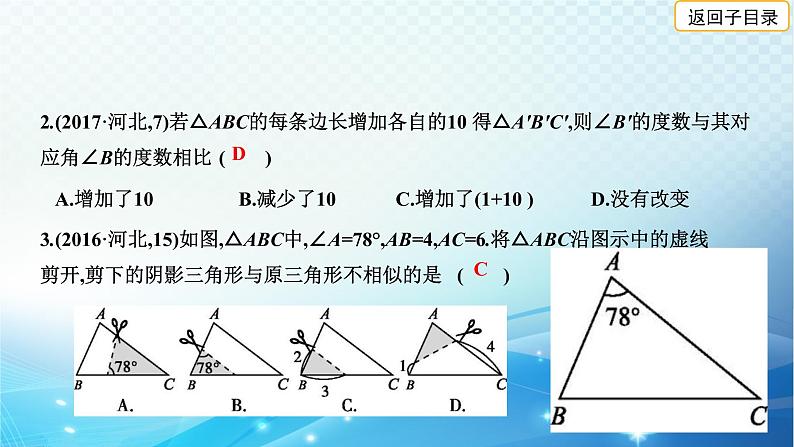
2.(2017·河北,7)若△ABC的每条边长增加各自的10 得△A'B'C',则∠B'的度数与其对应角∠B的度数相比(　　)
A.增加了10 B.减少了10 C.增加了(1+10 )D.没有改变
3.(2016·河北,15)如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(　　)
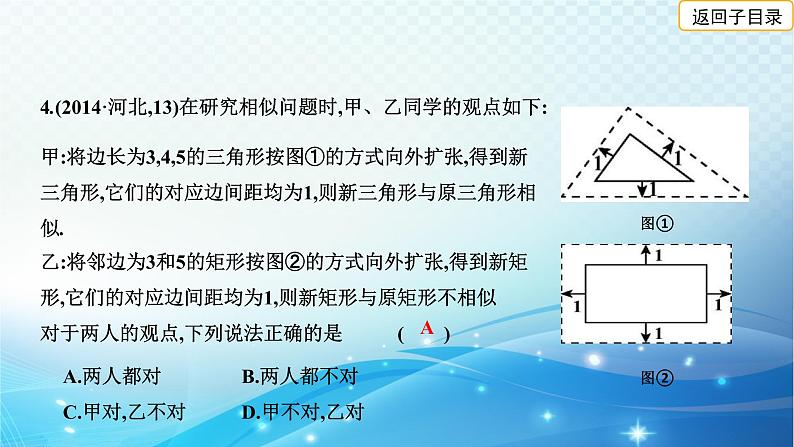
4.(2014·河北,13)在研究相似问题时,甲、乙同学的观点如下:
乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新矩形,它们的对应边间距均为1,则新矩形与原矩形不相似对于两人的观点,下列说法正确的是(　　)
甲:将边长为3,4,5的三角形按图①的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.
A.两人都对 B.两人都不对C.甲对,乙不对D.甲不对,乙对
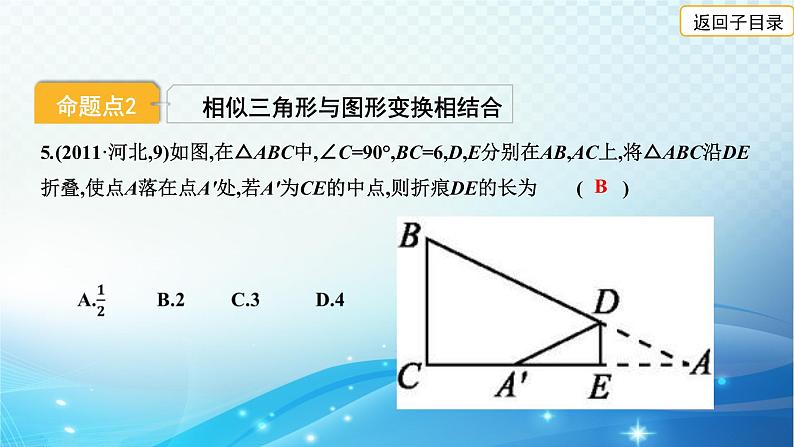
5.(2011·河北,9)如图,在△ABC中,∠C=90°,BC=6,D,E分别在AB,AC上,将△ABC沿DE折叠,使点A落在点A'处,若A'为CE的中点,则折痕DE的长为(　　)
6.(2020·河北,8)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是 (　　)
A.四边形NPMQB.四边形NPMR C.四边形NHMQD.四边形NHMR
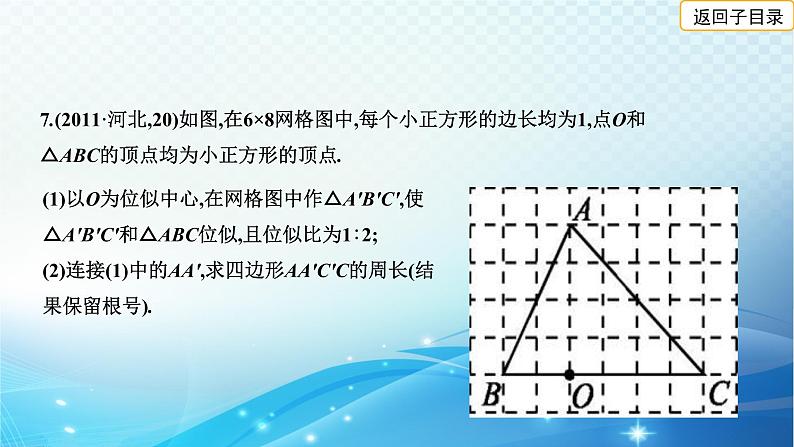
7.(2011·河北,20)如图,在6×8网格图中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.
(1)以O为位似中心,在网格图中作△A'B'C',使△A'B'C'和△ABC位似,且位似比为1∶2;(2)连接(1)中的AA',求四边形AA'C'C的周长(结果保留根号).
解:(1)如图所示,△A'B'C'即为所求;
8.(2012·河北,23)如图①,点E是线段BC的中点,分别以B,C为直角顶点的△EAB和△EDC均是等腰直角三角形,且在BC的同侧.
(1)AE和ED的数量关系为　　　　,AE和ED的位置关系为　　　　. (2)在图①中,以点E为位似中心,作△EGF与△EAB位似,点H是BC所在直线上的一点,连接GH,HD,分别得到了图②和图③.①在图②中,点F在BE上,△EGF与△EAB的相似比是1∶2,H是EC的中点.求证:GH=HD,GH⊥HD.②在图③中,点F在BE的延长线上,△EGF与△EAB的相似比是k∶1,若BC=2,请直接写出CH的长为多少时,恰好使得GH=HD且GH⊥HD(用含k的代数式表示).
1.线段的比:两条线段的比是两条线段的长度之比.
2.性质(1)相似三角形的对应角⑤　　　　; (2)相似三角形的对应线段(边、高、中线、角平分线)⑥　　　　; (3)相似三角形的周长比等于⑦　　　　,面积比等于⑧　　　　　　　. 
1.定义:三个角分别相等,三条边成比例的两个三角形叫做相似三角形,相似三角形对应边的比叫做相似比.
3.判定(1)⑨　　　　　　对应相等,两三角形相似; (2)两边对应成比例且⑩　　　　相等,两三角形相似; (3)三边 　　　　　　,两三角形相似; (4)两直角三角形的斜边和一条直角边对应成比例,两直角三角形相似.
2.性质(1)相似多边形的对应边 　　　　; (2)相似多边形的对应角 　　　　; (3)相似多边形周长的比 　　　　相似比,相似多边形面积的比等于 　　　　　　　　. 
1.定义:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形,相似多边形对应边的比叫做相似比.
2.性质(1)在平面直角坐标系中,如果位似变换是以原点为中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k;(2)位似图形上任意一对对应点到位似中心的距离之比等于 　　　　. 
3.找位似中心的方法:将两个图形的各组对应点连接起来,若它们所在的直线相交于一点,则该点就是位似中心.4.画位似图形的步骤(1)确定位似中心;(2)确定原图形的关键点;(3)确定位似比;(4)作出原图形中各关键点的对应点;(5)按原图形的连接顺序连接所作的各个对应点.【易错提示】两个位似图形的位似中心可能在图形内部,也可在图形外部、边上或顶点上.
A.只有①相似B.只有②相似C.都相似 D.都不相似
1.(2021·石家庄质检)已知图①②中各有两个三角形,其边长和角的度数已在图上标注,图②中AB,CD交于点O,对于各图中的两个三角形而言,下列说法正确的是(　　)
2.(2021·唐山模拟)如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是 (　　)
3.(2021·衡水模拟)如图,在△ABC中,点D,E分别为边AB,AC上的点,且DE∥BC,若AD=5,BD=10,DE=4,则BC的长为(　　)
A.8 B.10 C.12 D.16
4.(2021·唐山模拟)如图,在平行四边形ABCD中,点E为CD上一点,DE∶EC=2 ∶ 3,连接AE,BD,且AE,BD交于点F,则DF ∶ BF等于 (　　)
A.2 ∶ 5B.2 ∶ 3C.3 ∶ 5D.3 ∶ 2
5.(2021·河北模拟)如图,在Rt△ABC中,∠BAC=90°,AB = AC,E,D分别是BC,AC上的点,且∠AED=45°.
解:(1)证明:∵在Rt△ABC中,∠BAC=90°,AB=AC,∴∠B=∠C=45°.∵∠AEC=∠B+∠BAE=∠AED+∠CED,∠AED=45°,∴∠BAE=∠CED.∴△ABE∽△ECD.
1.(2021·邢台模拟)如图,若△ABC与△DEF是位似图形,则位似中心可能是(　　)
A.O1 B.O2 C.O3 D.O4
2.(2021·石家庄42中模拟)如图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作出与△AOB的位似比为k的位似△CDE,则位似中心的坐标和k的值分别为 (　　)
3.(2021·石家庄质检)如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA ∶ OA1=1 ∶ 3,则五边形ABCDE和五边形A1B1C1D1E1的面积比是(　　)
A.1 ∶ 2B.1 ∶ 3C.1 ∶ 4D.1 ∶ 9
4.(2021·河北模拟)如图,等腰Rt△ABC与等腰Rt△CDE是以点O为位似中心的位似图形,且位似比为k=1 ∶ 3,∠ACB=90°,BC=4,则点D的坐标是(　　)
A.(18,12) B.(16,12) C.(12,18) D.(12,16)
5.如图,△ABC在方格纸中
(1)请在方格纸中建立平面直角坐标系,使A(2,3),C(6,2),并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A'B'C';(3)计算△A'B'C'的面积S.
解:(1)画出如图所示的平面直角坐标系,点B的坐标是(2,1);
(2)画出的△A'B'C'如图所示;