2022-2023学年江苏省南京市九年级上册数学期末专项突破模拟卷（AB卷）含解析

这是一份2022-2023学年江苏省南京市九年级上册数学期末专项突破模拟卷（AB卷）含解析，共47页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。

2022-2023学年江苏省南京市九年级上册数学期末专项突破模拟卷（A卷）
一、选一选（共10题；共30分）
1. 如果两个相似三角形对应边比为2：3，那么这两个相似三角形面积的比是（   ）
A. 2：3 B. C. 4：9 D. 8：27
2. 将抛物线向右平移1个单位，再向下平移3个单位得到的抛物线表达式是（ ）
A. B. C. D.
3. 已知tanα=6.866，用计算器求锐角α（到1″），按键顺序正确的是（　　）
A.
B
C.
D.
4. 如图所示的图案中，没有能由基本图形通过平移方法得到的图案是（　　）
A. vB. C. D.
5. 抛物线y=x2－bx+8的顶点在x轴上，取b的值一定为(　　 )
A. 4 B. -4 C. 2或-2 D. 或
6. 如图所示的四个图形中，没有能通过基本图形平移得到的是（　　）
A. B. C. D.
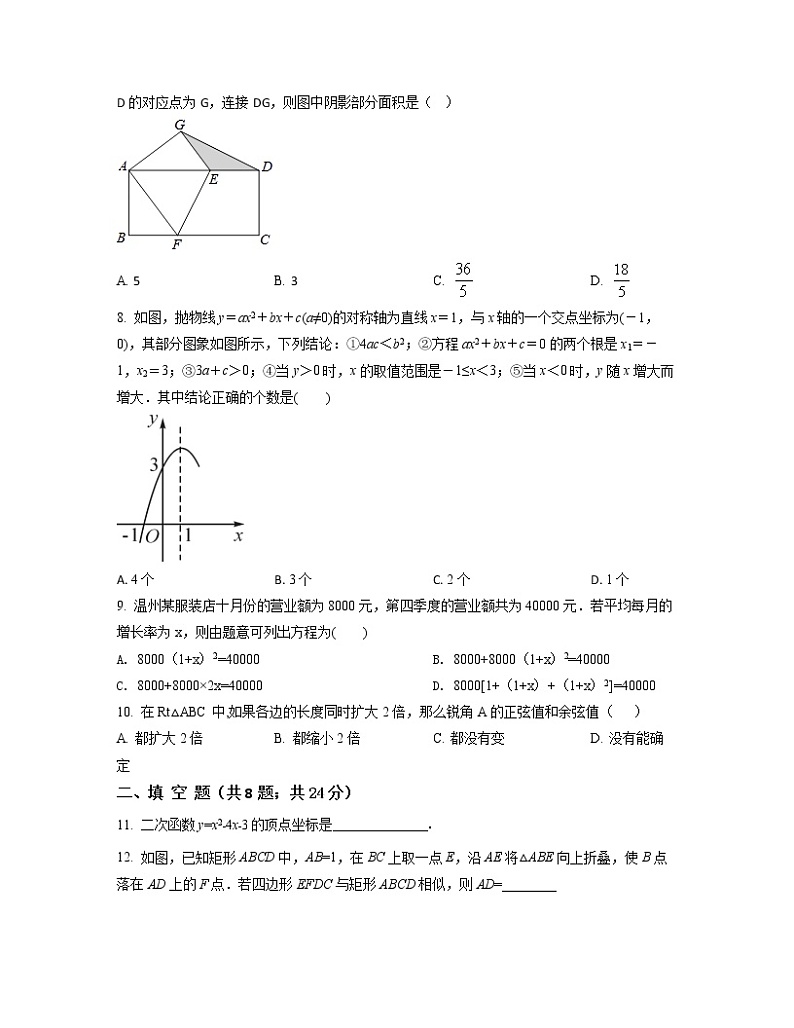
7. 如图，矩形纸片ABCD中，AB=4，BC=8，将纸片折叠，使点C与点A重合，折痕为EF，点D的对应点为G，连接DG，则图中阴影部分面积是（   ）

A. 5 B. 3 C. D.
8. 如图，抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2＋bx＋c＝0的两个根是x1＝－1，x2＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
9. 温州某服装店十月份的营业额为8000元，第四季度的营业额共为40000元．若平均每月的增长率为x，则由题意可列出方程为( )
A. 8000（1+x）2=40000 B. 8000+8000（1+x）2=40000
C. 8000+8000×2x=40000 D. 8000[1+（1+x）+（1+x）2]=40000
10. 在Rt△ABC中,如果各边的长度同时扩大2倍，那么锐角A的正弦值和余弦值（ ）
A. 都扩大2倍 B. 都缩小2倍 C. 都没有变 D. 没有能确定
二、填 空 题（共8题；共24分）
11. 二次函数y=x2﹣4x﹣3的顶点坐标是______________．
12. 如图，已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点．若四边形EFDC与矩形ABCD相似，则AD=________

13. 如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=42°，则∠OAC的度数是________．

14. 已知关于x的方程x2－x－2＝0的两个根为x1、x2，则x1+ x2－x1x2＝_____．
15. 若关于x的方程kx2+2x+1=0有两个实根，则k的取值范围是________．
16. 近视眼镜的度数y（度）与镜片焦距x（m）成反比例（即），已知200度近视眼镜的镜片焦距为0.5m，则y与x之间的函数关系式是______．
17. 某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（没有包括门）总长为27m，则能建成的饲养室面积为________ m2 ．

18. 如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称O处，折痕为EF．若菱形ABCD的边长为2cm，∠A=120°，则EF=_______cm．

三、解 答 题:
19. 如图，已知反比例函数（k1＞0）与函数相交于A、B两点，AC⊥x轴于点C. 若△OAC的面积为1，且tan∠AOC＝2 .
（1）求出反比例函数与函数的解析式；
（2）请直接写出B点的坐标，并指出当x为何值时，反比例函数y1的值大于函数y2的值.

20. 如图，在△ABC中，D为AC边上一点，∠DBC=∠A．
（1）求证：△BDC∽△ABC；
（2）如果BC=， AC=3，求CD的长．

21. 如图，在△ABC中，D是边AB中点，DE∥BC交AC于点E.求证：AE=EC

22. 如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件PQMN，使正方形PQMN的边QM在BC上，其余两个项点P，N分别在AB，AC上．求这个正方形零件PQMN面积S．

23. 解方程：x2+x﹣2=0．
24. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形．
（1）如图1，在半对角四边形ABCD中，∠B＝∠D，∠C＝∠A，求∠B与∠C的度数之和；

（2）如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．

求证：四边形DBCF是半对角四边形；
（3）如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当DH＝BG时，求△BGH与△ABC的面积之比．

25 综合题．
（1）如图，在方格纸中先通过________，由图形A得到图形B，再由图形B先________（怎样平移），再________（怎样旋转）得到图形C（对于平移变换要求回答出平移方向和平移的距离；对于旋转变换要求回答出旋转、旋转方向和旋转角度）；
（2）如图，如果点P、P3的坐标分别为（0，0）、（2，1），写出点P2的坐标是________；
（3）图形B能绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是________；
（4）图形A能绕某点R顺时针旋转90°得到图形C，则点R的坐标是________； 注：方格纸中的小正方形的边长为1个单位长度．











2022-2023学年江苏省南京市九年级上册数学期末专项突破模拟卷（A卷）
一、选一选（共10题；共30分）
1. 如果两个相似三角形对应边的比为2：3，那么这两个相似三角形面积的比是（   ）
A. 2：3 B. C. 4：9 D. 8：27
【正确答案】C

【详解】解：两个相似三角形面积的比是=4：9．
故选C．
本题考查相似三角形的性质．
2. 将抛物线向右平移1个单位，再向下平移3个单位得到的抛物线表达式是（ ）
A. B. C. D.
【正确答案】B

【分析】先确定抛物线y=2x2的顶点坐标为（0，0），平移后的顶点的坐标为（1，-3），然后根据顶点式写出平移后抛物线的解析式.
【详解】解：∵y=2x2的顶点是（0，0）
∴向右平移1个单位，再向下平移3个单位后的抛物线的顶点是（1，-3）,代入二次函数顶点式y=a(x-h)2+k中
∴y=2(x-1)2-3
故选B.
解决此类题目的关键是将二次函数图象的平移转化为顶点的平移，再根据顶点的平移确定平移后的抛物线的解析式.
3. 已知tanα=6.866，用计算器求锐角α（到1″），按键顺序正确的是（　　）
A.
B.
C.
D.
【正确答案】D

【详解】先按第二功能键2nd键，再按三角函数tan 键，再依次输入6.866，再按“=”就可以出来答案α，
故选D.
4. 如图所示的图案中，没有能由基本图形通过平移方法得到的图案是（　　）
A. B. C. D.
【正确答案】B

详解】A、可以通过平移得到，没有符合题意；
B、没有能通过平移得到，符合题意；
C、可以通过平移得到，没有符合题意；
D、可以通过平移得到，没有符合题意，
故选：B．
5. 抛物线y=x2－bx+8的顶点在x轴上，取b的值一定为(　　 )
A. 4 B. -4 C. 2或-2 D. 或
【正确答案】D

【详解】∵抛物线y=x2-bx+8的顶点在x轴上，
∴△=（-b)2-4×8=b2-32=0，解得b= ，
故选D．
本题考查的是抛物线与x轴的交点问题，能利用根的判别式判断抛物线与x轴的交点问题是解答此题的关键．
6. 如图所示的四个图形中，没有能通过基本图形平移得到的是（　　）
A. B. C. D.
【正确答案】B

【详解】A、能通过其中一个正六边形平移得到，故此选项错误； B、没有能通过其中一个长方形平移得到，故此选项符合题意；
C、能通过其中一个平行四边形平移得到，故此选项错误；
D、能通过其中一个正方形平移得到，故此选项错误．
故选B．
7. 如图，矩形纸片ABCD中，AB=4，BC=8，将纸片折叠，使点C与点A重合，折痕为EF，点D对应点为G，连接DG，则图中阴影部分面积是（   ）

A. 5 B. 3 C. D.
【正确答案】D

【详解】过点G作GH⊥AD于点H，
由题意知，AF=FC，AB=CD=AG=4，BC=AD=8，
在Rt△ABF中，由勾股定理知AB2+BF2=AF2 ， 即42+（8﹣AF）2=AF2 ，
解得AF=5，
∵∠BAF+∠FAE=∠FAE+∠EAG=90°，
∴∠BAF=∠EAG，
∵∠B=∠AGE=90°，AB=AG，
∴△BAF≌△GAE，
∴AE=AF=5，ED=GE=3，
∵S△GAE=AG•GE=AE•GH
∴GH=，
∴S△GED= ED•GH= ×3×= ，
故选D．

8. 如图，抛物线y＝ax2＋bx＋c(a≠0)的对称轴为直线x＝1，与x轴的一个交点坐标为(－1，0)，其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2＋bx＋c＝0的两个根是x1＝－1，x2＝3；③3a＋c＞0；④当y＞0时，x的取值范围是－1≤x＜3；⑤当x＜0时，y随x增大而增大．其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
【正确答案】B

【详解】解：∵抛物线与x轴有2个交点，
∴b2﹣4ac＞0，所以①正确；
∵抛物线的对称轴为直线x=1，而点（﹣1，0）关于直线x=1的对称点的坐标为（3，0），
∴方程ax2+bx+c=0的两个根是x1=﹣1，x2=3，所以②正确；
∵x=﹣=1，即b=﹣2a，而x=﹣1时，y=0，即a﹣b+c=0，
∴a+2a+c=0，所以③错误；
∵抛物线与x轴的两点坐标为（﹣1，0），（3，0），
∴当﹣1＜x＜3时，y＞0，所以④错误；
∵抛物线的对称轴为直线x=1，
∴当x＜1时，y随x增大而增大，所以⑤正确．
故选：B．
本题考查了二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．
9. 温州某服装店十月份的营业额为8000元，第四季度的营业额共为40000元．若平均每月的增长率为x，则由题意可列出方程为( )
A. 8000（1+x）2=40000 B. 8000+8000（1+x）2=40000
C. 8000+8000×2x=40000 D. 8000[1+（1+x）+（1+x）2]=40000
【正确答案】D

【详解】试题解析：设平均每月的增长率为x，
则十一月份的营业额为8000（1+x），
十二月份的营业额为8000（1+x）2，
由此列出方程：8000[1+（1+x）+（1+x）2]=40000．
故选D．
10. 在Rt△ABC中,如果各边的长度同时扩大2倍，那么锐角A的正弦值和余弦值（ ）
A. 都扩大2倍 B. 都缩小2倍 C. 都没有变 D. 没有能确定
【正确答案】C

【详解】∵Rt△ABC中，若各边的长度同时都扩大2倍，
∴扩大后形成的三角形与原三角形相似，
∴锐角A的正弦与余弦的比值没有变，
故选C．
本题产要考查相似及锐角三角函数，解答此题的关键是熟知三角函数值是一个比值，与角的边长无关.
二、填 空 题（共8题；共24分）
11. 二次函数y=x2﹣4x﹣3的顶点坐标是______________．
【正确答案】(2,-7)

【详解】试题分析：原式化为顶点式解析式，即为y=(x-2)2-7,所以其顶点坐标是（2,﹣7）．
考点：求二次函数的顶点坐标.
12. 如图，已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点．若四边形EFDC与矩形ABCD相似，则AD=________

【正确答案】

【分析】可设AD=x，根据四边形EFDC与矩形ABCD相似，可得比例式，求解即可．
【详解】∵沿AE将△ABE向上折叠，使B点落在AD上F点，
∴四边形ABEF是正方形，
∵AB=1，
设AD=x，则FD=x−1，FE=1，
∵四边形EFDC与矩形ABCD相似，
∴，
，
解得x1=，x2= (负值舍去)，
经检验x1=是原方程的解．
本题考查了折叠的性质及相似多边形的性质，熟练掌握性质定理是解题的关键．
13. 如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=42°，则∠OAC的度数是________．

【正确答案】21°

【详解】∵∠AOB=42°，
∴∠ACB=∠AOB=21°．
∵AO∥BC，
∴∠OAC=∠ACB=21°．
故答案为21°．
14. 已知关于x的方程x2－x－2＝0的两个根为x1、x2，则x1+ x2－x1x2＝_____．
【正确答案】3

【详解】试题分析：本题考查了根与系数的关系，解题的关键是根据根与系数的关系找出x1+x2=1，x1x2=-2．本题属于基础题，难度没有大，解决该类型题目时，只需能熟练的运用根与系数的关系即可.根据根与系数的关系找出x1+x2=1，x1x2=-2，将其代入x1+x2-x1x2中即可得出结论．
∵x1、x2为关于x的方程x2-x-2=0的两个根，
∴x1+x2-x1x2=-−11=1，x1x2==-2，
∴x1+x2-x1x2=1-（-2）=3．
故答案为3．
考点：根与系数的关系．
15. 若关于x的方程kx2+2x+1=0有两个实根，则k的取值范围是________．
【正确答案】k≤1且k≠0

【详解】试题解析：依题意列方程组

解得k＜1且k≠0．
考点：根的判别式．
16. 近视眼镜的度数y（度）与镜片焦距x（m）成反比例（即），已知200度近视眼镜的镜片焦距为0.5m，则y与x之间的函数关系式是______．
【正确答案】．

【详解】由于点（0.5，200）适合这个函数解析式，则k=0.5×200=100，∴．
故眼镜度数y与镜片焦距x之间的函数关系式为：．
17. 某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1m宽的门．已知计划中的材料可建墙体（没有包括门）总长为27m，则能建成的饲养室面积为________ m2 ．

【正确答案】75

【详解】试题分析：首先设垂直于墙面的长度为x，则根据题意可得：平行于墙面的长度为（30－3x），则S=x（30－3x）=－3+75，,则当x=5时，y有值，值为75，即饲养室的面积为75平方米.
考点：一元二次方程的应用.

18. 如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称O处，折痕为EF．若菱形ABCD的边长为2cm，∠A=120°，则EF=_______cm．

【正确答案】

【详解】如图，连接AO交EF于点P，

由菱形和折叠对称的性质，知四边形AEOF是菱形，且AP=OP．
∵点A恰好落在菱形的对称O处，
∴AE=BE．
∵AB=2，∠A=120°，
∴Rt△AEP中，AE=1，∠AEP=30°．
∴，
∴，
∴EF＝．
三、解 答 题:
19. 如图，已知反比例函数（k1＞0）与函数相交于A、B两点，AC⊥x轴于点C. 若△OAC的面积为1，且tan∠AOC＝2 .
（1）求出反比例函数与函数的解析式；
（2）请直接写出B点的坐标，并指出当x为何值时，反比例函数y1的值大于函数y2的值.

【正确答案】（1）；；（2）B点的坐标为（－2，－1）；当0＜x＜1和x＜－2时，y1＞y2.

【分析】（1）根据tan∠AOC＝＝2，△OAC的面积为1，确定点A的坐标，把点A的坐标分别代入两个解析式即可求解；
（2）根据两个解析式求得交点B的坐标，观察图象，得到当x为何值时，反比例函数y1的值大于函数y2的值．
【详解】解：（1）在Rt△OAC中，设OC＝m．
∵tan∠AOC＝＝2，∴AC＝2×OC＝2m．
∵S△OAC＝×OC×AC＝×m×2m＝1，∴m2＝1．∴m＝1（负值舍去）．
∴A点的坐标为（1，2）．
把A点的坐标代入中，得k1＝2．
∴反比例函数的表达式为．
把A点坐标代入中，得k2＋1＝2，∴k2＝1．
∴函数的表达式．
（2）B点的坐标为（－2，－1）．
当0＜x＜1和x＜－2时，y1＞y2．
本题考查反比例及函数的的应用；待定系数法求解析式；图象的交点等，掌握反比例及函数的性质是本题的解题关键．
20. 如图，在△ABC中，D为AC边上一点，∠DBC=∠A．
（1）求证：△BDC∽△ABC；
（2）如果BC=， AC=3，求CD的长．

【正确答案】（1）详见解析；（2）CD=2.

【分析】（1）根据相似三角形的判定得出即可；
（2）根据相似得出比例式，代入求出即可．
【详解】证明：（1）∵∠DBC=∠A，∠C=∠C，
∴△BDC∽△ABC；
（2）∵△BDC∽△ABC，
∴ ，
∴ ，
∴CD=2．
考核知识点：相似三角形的判定和性质.
21. 如图，在△ABC中，D是边AB的中点，DE∥BC交AC于点E.求证：AE=EC

【正确答案】证明见解析.

【分析】先判定△ADE和△ABC相似，再根据相似三角形对应边成比例列式求解即可．
【详解】∵DE∥BC，
∴△ADE∽△ABC，
∴，
∵D点是边AB的中点，
∴AB=2AD，
∴，
∴AC=2AE，
∴AE=CE．
22. 如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件PQMN，使正方形PQMN的边QM在BC上，其余两个项点P，N分别在AB，AC上．求这个正方形零件PQMN面积S．

【正确答案】正方形零件PQMN面积是2304mm2.

【详解】试题分析：PN与AD交于点E，如图，设MN=xmm，则AE=AD﹣ED=80﹣x，再证明△APN∽△ABC，利用相似比可表示出PN=（80﹣x），根据正方形的性质得到（80﹣x）=x，然后正方形的面积公式进行解答即可．
试题解析：PN与AD交于点E，如图，设MN=xmm，
易得四边形MNED为矩形，则ED=MN=x，
∴AE=AD﹣ED=80﹣x，
∵PN∥BC，
∴△APN∽△ABC，
∴ ，即 ，
∴PN=（80﹣x），
∵PN=MN，
∴（80﹣x）=x，
解得x=48，
故正方形零件PQMN面积S为：48×48=2304（mm2），
答：正方形零件PQMN面积S是2304mm2.
23. 解方程：x2+x﹣2=0．
【正确答案】x1=1，x2=﹣2．

【详解】分析：方程左边利用十字相乘法分解因式后，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元方程来求解．
本题解析：分解因式得：（x﹣1）（x+2）=0，可得x﹣1=0或x+2=0，解得：x1=1，x2=﹣2．
24. 有两个内角分别是它们对角的一半的四边形叫做半对角四边形．
（1）如图1，在半对角四边形ABCD中，∠B＝∠D，∠C＝∠A，求∠B与∠C的度数之和；

（2）如图2，锐角△ABC内接于⊙O，若边AB上存在一点D，使得BD＝BO．∠OBA的平分线交OA于点E，连结DE并延长交AC于点F，∠AFE＝2∠EAF．

求证：四边形DBCF是半对角四边形；
（3）如图3，在（2）的条件下，过点D作DG⊥OB于点H，交BC于点G．当DH＝BG时，求△BGH与△ABC的面积之比．

【正确答案】（1）∠B与∠C的度数之和120°；（2）证明见解析；（3）.

【详解】试题分析：（1）在半对角四边形ABCD中，∠B=∠D，∠C=∠A；根据四边形的内角和为360°，得出∠B与∠C的度数之和；
（2）如图连接OC，根据条件先证△BED≌△BEO，再根据全等三角形的性质得出∠BCF=∠BOE=∠BDE；设∠EAF=α，则∠AFE=2∠EAF=2α得出∠EFC=180°-∠AFE=180°-2α；再根据OA=OC得出∠OAC=∠OCA=α， 根据三角形内角和得出∠AOC=180°-∠OAC-∠OCA=180°-2α；从而得证.
（3）如图，过点作OM⊥BC于点M，由四边形DBCF是半对角四边形，得出∠ABC+∠ACB=120°，∠BAC=60°，∠BOC=2∠BAC=120°；再由OB=OC，得出∠OBC=∠OCB=30°，BC=2BM=BO=BD；根据△DBG～△CBA得出答案.
试题解析：（1）在半对角四边形ABCD中，∠B=∠D，∠C=∠A，
∵∠A+∠B+∠C+∠D=360°，
∴3∠B+3∠C=360°，
∴∠B+∠C=120°，
即∠B与∠C度数之和120°；
（2）在△BED和△BEO中，
，
∴△BED≌△BEO（SAS），
∴∠BDE=∠BOE，
又∵∠BCF=∠BOE，
∴∠BCF=∠BDE，
如图，连结OC，
设∠EAF=α，.则∠AFE=2∠EAF=2α，
∴∠EFC=180°-∠AFE=180°-2α，
∵OA=OC,
∴∠OAC=∠OCA=α，
∴∠AOC=180°-∠OAC-∠OCA=180°-2α，
∴∠ABC=∠AOC=∠EFC.
∴四边形DBCF是半对角四边形；

（3）如图，作过点OM⊥BC于点M.
∵四边形DBCF是半对角四边形，
∴∠ABC+∠ACB=120°，
∴∠BAC=60°，
∴∠BOC=2∠BAC=120°，
∵OB=OC，
∴∠OBC=∠OCB=30°，
∴BC=2BM=BO=BD，
∵DG⊥OB，
∴∠HGB=∠BAC=60°，
∵∠DBG=∠CBA，
∴△DBG∽△CBA，
∴ ，
∵DH=BG，BG=2HG，
∴DG=3HG，
∴，
∴.

25. 综合题．
（1）如图，在方格纸中先通过________，由图形A得到图形B，再由图形B先________（怎样平移），再________（怎样旋转）得到图形C（对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转、旋转方向和旋转角度）；
（2）如图，如果点P、P3的坐标分别为（0，0）、（2，1），写出点P2的坐标是________；
（3）图形B能绕某点Q顺时针旋转90°得到图形C，则点Q的坐标是________；
（4）图形A能绕某点R顺时针旋转90°得到图形C，则点R的坐标是________； 注：方格纸中的小正方形的边长为1个单位长度．

【正确答案】（1）向上平移4个单位长；向右平移4个单位长度；绕点P2顺时针旋转90°；（2）（4，4）；（3）（2，2）；（4）（4，0）.

【详解】试题分析：（1）如图，根据方格纸中A和B的位置可以确定图形变换方式；然后根据B和C也可以确定图形变换方式；
（2）根据（1）和已知条件首先确定P、P3和P2的关系，然后就可以确定P2的坐标；
（3）由于图形B能绕某点Q顺时针旋转90°得到图形C，首先可以确定两组旋转对应点，然后根据旋转的性质即可确定旋转Q的坐标；
（4）由于图形A能绕某点R顺时针旋转90°得到图形C，首先可以确定两组旋转对应点的坐标，然后根据旋转的性质即可确定点R的坐标．
试题解析：（1）根据题意可知，向上平移4个单位长度图形A得到图形B，图形B向右平移4个单位长度，再绕点P2顺时针旋转90°得到图形C．
故答案为向上平移4个单位长，向右平移4个单位长度，绕点P2顺时针旋转90°．
（2）根据题意建立如图坐标系，根据图象可知P2（4，4）．
故答案为（4，4）．
（3）观察图形可知旋转Q（2，2）．
故答案为（2，2）．
（4）观察图形可知旋转R（4，0）．
故答案为（4，0）．
本题分别考查了旋转、平移的性质、也考查了坐标与图形变换之间的关系，解题时首先利用平移、旋转的性质确定变换后的图形的位置，然后利用坐标与图形变换之间的关系确定坐标．












2022-2023学年江苏省南京市九年级上册数学期末专项突破模拟卷（B卷）
一、选一选（本大题共10小题，每小题3分，共30分）
1. 方程的解为(　 　)
A. B. C. ， D. ，
2. 下列图形中，既是轴对称图形又是对称图形的是（ ）
A. 平行四边形 B. 菱形 C. 等边三角形 D. 等腰直角三角形
3. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A＇OB＇，若∠AOB=15°，则∠AOB＇的度数是（ ）

A. 25° B. 30° C. 35° D. 40°
4. 下列说确的是 （ ）
A. “有交通信号的路口遇到红灯”是必然
B. 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次
C. 投掷一枚硬币正面朝上是随机
D. 明天太阳从东方升起是随机
5. 已知一元二次方程有一个根为2，则另一根为（　　）
A -4 B. -2 C. 4 D. 2
6. 若点M在抛物线的对称轴上，则点M的坐标可能是（　 　）
A （3，-4） B. （-3，0） C. （3，0） D. （0，-4）
7. 如图，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则∠A的度数为（ ）

A. 60° B. 70° C. 120° D. 140°
8. 将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度，得到的函数表达式是（　　）
A y=（x+3）2﹣2 B. y=（x+3）2+2
C. y=（x﹣1）2+2 D. y=（x﹣1）2﹣2
9. 如图，菱形ABCD中，∠B＝60°，AB＝4，以AD为直径的⊙O交CD于点E，则的长为（　　）

A. B. C. D.
10. 如图，直线的解析式为，它与轴和轴分别相交于两点，平行于直线的直线从原点出发，沿轴的正方向以每秒1个单位长度的速度运动.它与轴和轴分别相交于两点，运动时间为秒（），以为斜边作等腰直角三角形（两点分别在两侧），若和的重合部分的面积为，则与之间的函数关系的图象大致是（ ）


A. B. C. D.
二、填 空 题（本大题共6小题，每小题4分，共24分）
11. 已知点P（a+1，1）关于原点的对称点在第四象限，则a的取值范围是_____．
12. 若一元二次方程ax2﹣bx﹣2018＝0有一个根为x＝﹣1，则a+b＝____．
13. 若关于的一元二次方程(m-1)x2-4x+1=0有两个没有相等的实数根，则m的取值范围为_____________．
14. 如图，在△ABC中，AB=4，BC=7，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为__________．


15. 如图，中，，以点为圆心的圆与相切，则的半径为________.

16. 有一个二次函数图象，三位同学分别说了它的一些特点：
甲：与轴只有一个交点；
乙：对称轴是直线；
丙：与y轴的交点到原点的距离为3．
满足上述全部特点的二次函数的解析式为______________________．
三、解 答 题（一）（本大题共3小题，每小题6分，共18分）
17. 解一元二次方程：．
18. 已知抛物线y＝ax2+bx+c点A（1，0），B（﹣1，0），C（0，﹣2）．求此抛物线的函数解析式和顶点坐标．
19. 如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC=3．
（1）以BC边上一点O为圆心作⊙O，使⊙O分别与AC、AB都相切 (要求：尺规作图，保留作图痕迹，没有写作法) ；
（2）求⊙O的面积．

四、解 答 题（二）（本大题共3小题，每小题7分，共21分）
20. 车辆润扬大桥收费站时，4个收费通道 A．B、C、D中，可随机选择其中的一个通过．
（1）一辆车此收费站时，选择 A通道通过概率是 ；
（2）求两辆车此收费站时，选择没有同通道通过的概率．
21. 某小区在绿化工程中有一块长为，宽为的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为，两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．

22. 正方形ABCD的边长为3，E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.
（1）求证：EF=FM
（2）当AE=1时，求EF的长．

五、解 答 题（三）（本大题共3小题，每小题9分，共27分）
23. 某商场购进一批单价为4元的日用品．若按每件5元的价格，每月能卖出3万件；若按每件6元的价格，每月能卖出2万件，假定每月件数y（件）与价格x（元/件）之间满足函数关系．
（1）试求y与x之间的函数关系式；
（2）当价格定为多少时，才能使每月的利润？每月的利润是多少？
24. 如图⊙O是△ABC的外接圆，∠ABC＝45°，延长BC于D，连接AD，使得AD∥OC，AB交OC于E．
（1）求证：AD与⊙O相切；
（2）若AE＝2，CE＝2．求⊙O的半径和AB的长度．

25. 如图，直线l： 与x轴、y轴分别交于点B、C，B、C两点的抛物线 与x轴的另一个交点为A．

（1）求该抛物线的解析式；
（2）若点P在直线l下方的抛物线上，过点P作轴交l于点D，轴交l于点E，求的值；
（3）设F为直线l上的点，点P仍在直线l下方的抛物线上，以A、B、P、F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若没有能，请说明理由．





2022-2023学年江苏省南京市九年级上册数学期末专项突破模拟卷（B卷）
一、选一选（本大题共10小题，每小题3分，共30分）
1. 方程的解为(　 　)
A. B. C. ， D. ，
【正确答案】C

【详解】试题解析：
分解因式得：x(x+1)=0，
∴x=0，x+1=0，
解方程得：
故选C.
2. 下列图形中，既是轴对称图形又是对称图形的是（ ）
A. 平行四边形 B. 菱形 C. 等边三角形 D. 等腰直角三角形
【正确答案】B

【详解】试题解析：A. 没有是轴对称图形，是对称图形，故此选项错误，没有合题意；
B. 是轴对称图形，也是对称图形，故此选项正确，符合题意；
C. 轴对称图形，没有是对称图形，故此选项错误，没有合题意；
D. 无法确定是轴对称图形，也没有是对称图形，故此选项错误，没有合题意.
故选B.
3. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A＇OB＇，若∠AOB=15°，则∠AOB＇的度数是（ ）


A. 25° B. 30° C. 35° D. 40°
【正确答案】B

【详解】解：∵将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′，
∴∠A′OA=45°，∠AOB=∠A′OB′=15°，
∴∠AOB′=∠A′OA-∠A′OB′=45°-15°=30°，
故选B．
4. 下列说确的是 （ ）
A. “有交通信号的路口遇到红灯”是必然
B. 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次
C. 投掷一枚硬币正面朝上是随机
D. 明天太阳从东方升起是随机
【正确答案】C

【详解】试题解析：A. “有交通信号的路口遇到红灯”是随机, 说法错误.
B. 已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次,说法错误.
C. 投掷一枚硬币正面朝上是随机,说确.
D. 明天太阳从东方升起是必然.说法错误.
故选C.
5. 已知一元二次方程有一个根为2，则另一根为（　　）
A. -4 B. -2 C. 4 D. 2
【正确答案】D

【详解】试题解析: 设关于x的一元二次方程的另一个根为t，则
解得t=2.
故选D.
点睛：一元二次方程两根分别是

6. 若点M在抛物线的对称轴上，则点M的坐标可能是（　 　）
A. （3，-4） B. （-3，0） C. （3，0） D. （0，-4）
【正确答案】B

【详解】试题解析:
∴对称轴为x=-3，
∵点M在对称轴上,
∴M点横坐标为-3，
故选B.
7. 如图，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则∠A的度数为（ ）

A. 60° B. 70° C. 120° D. 140°
【正确答案】A

【详解】试题解析:设
则



解得:
故选A.
点睛:圆内接四边形的对角互补.
8. 将二次函数y=x2+2x﹣1的图象沿x轴向右平移2个单位长度，得到的函数表达式是（　　）
A. y=（x+3）2﹣2 B. y=（x+3）2+2
C. y=（x﹣1）2+2 D. y=（x﹣1）2﹣2
【正确答案】D

【分析】根据题目中的函数解析式，可以先化为顶点式，然后再根据左加右减的方法进行解答即可得到平移后的函数解析式．
【详解】解：∵y=x2+2x-1=（x+1）2-2，
∴二次函数y=x2+2x-1的图象沿x轴向右平移2个单位长度，得到的函数表达式是：y=（x+1-2）2-2=（x-1）2-2，
故选D．
本题考查二次函数的图象与几何变换，解答本题的关键是明确二次函数平移的特点，左加右减、上加下减，注意一定将函数解析式化为顶点式之后再平移．
9. 如图，菱形ABCD中，∠B＝60°，AB＝4，以AD为直径的⊙O交CD于点E，则的长为（　　）

A. B. C. D.
【正确答案】B

【分析】连接OE，由菱形的性质得出∠D＝∠B＝60°，AD＝AB＝4，得出OA＝OD＝2，由等腰三角形的性质和三角形内角和定理求出∠DOE＝60°，再由弧长公式即可得出答案．
【详解】解：连接OE，如图所示：

∵四边形ABCD是菱形，
∴∠D＝∠B＝60°，AD＝AB＝4，
∴OA＝OD＝2，
∵OD＝OE，
∴∠OED＝∠D＝60°，
∴∠DOE＝180°﹣2×60°＝60°，
∴ 的长＝＝；
故选B．
本题考查弧长公式、菱形的性质、等腰三角形的性质等知识；熟练掌握菱形的性质，求出∠DOE的度数是解决问题的关键．
10. 如图，直线的解析式为，它与轴和轴分别相交于两点，平行于直线的直线从原点出发，沿轴的正方向以每秒1个单位长度的速度运动.它与轴和轴分别相交于两点，运动时间为秒（），以为斜边作等腰直角三角形（两点分别在两侧），若和的重合部分的面积为，则与之间的函数关系的图象大致是（ ）


A B. C. D.
【正确答案】C

【分析】分别求出0＜t≤2和2＜t≤4时，S与t的函数关系式即可爬判断．
【详解】解：当0＜t≤2时，S=t2，
当2＜t≤4时，S=t2﹣（2t﹣4）2=﹣t2+8t﹣8，
观察图象可知，S与t之间的函数关系的图象大致是C．
故答案为C．
二、填 空 题（本大题共6小题，每小题4分，共24分）
11. 已知点P（a+1，1）关于原点的对称点在第四象限，则a的取值范围是_____．
【正确答案】

【详解】试题解析: ∵P（，1关于原点对称的点在第四象限，
∴P点在第二象限，
∴a+1<0,
解得：a<−1，
故答案为: a<−1.
12. 若一元二次方程ax2﹣bx﹣2018＝0有一个根为x＝﹣1，则a+b＝____．
【正确答案】2018

【分析】把x=-1代入方程，整理即可求出a+b的值．
【详解】解：把x=-1代入方程有：
a+b-2018=0，
即a+b=2018．
故答案是：2018．
本题考查的是一元二次方程的解，把方程的解代入方程，可以求出代数式的值．
13. 若关于的一元二次方程(m-1)x2-4x+1=0有两个没有相等的实数根，则m的取值范围为_____________．
【正确答案】且

【详解】试题解析: ∵一元二次方程有两个没有相等的实数根，
∴m−1≠0且△=16−4(m−1)>0，解得m<5且m≠1，
∴m的取值范围为m<5且m≠1.
故答案为:m<5且m≠1.
点睛:一元二次方程
方程有两个没有相等的实数根时:
14. 如图，在△ABC中，AB=4，BC=7，∠B=60°，将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为__________．


【正确答案】3

【详解】由旋转的性质可得：AD=AB，
，
∴△ABD是等边三角形，
∴BD=AB，
∵AB=4，BC=7，
∴CD=BC−BD=7−4=3.
故3.
15. 如图，中，，以点为圆心的圆与相切，则的半径为________.

【正确答案】

【详解】试题解析: 在△ABC中，

∵AB=5，BC=3，AC=4，


如图：设切点为D，连接CD，
∵AB是C的切线，
∴CD⊥AB，

∴AC⋅BC=AB⋅CD，
即
∴的半径为
故答案为:
点睛:如果三角形两条边的平方和等于第三条边的平方,那么这个三角形是直角三角形.
16. 有一个二次函数的图象，三位同学分别说了它的一些特点：
甲：与轴只有一个交点；
乙：对称轴是直线；
丙：与y轴的交点到原点的距离为3．
满足上述全部特点的二次函数的解析式为______________________．
【正确答案】或

【详解】试题解析: ∵二次函数的对称轴为直线x=3，
∴k=3，
∴二次函数的解析式为
∵与y轴的交点到原点的距离为3，
∴与y轴交于点(0,3)或(0,−3)，
把(0,3)代入得，

把(0,−3)代入得，

∴解析式为：或.
故答案为或.
三、解 答 题（一）（本大题共3小题，每小题6分，共18分）
17. 解一元二次方程：．
【正确答案】

【分析】用直配方法解方程即可.
【详解】解:原方程可化为：
，
∴，
解得：．
18. 已知抛物线y＝ax2+bx+c点A（1，0），B（﹣1，0），C（0，﹣2）．求此抛物线的函数解析式和顶点坐标．
【正确答案】抛物线顶点坐标为（0，-2）

【分析】利用待定系数法即可求出二次函数解析式，化为顶点式即可求出抛物线的顶点坐标．
【详解】把点A（1，0）、B（-1，0）、C（0，-2）的坐标,
分别代入得：，
解得：，
∴二次函数的解析式为．
∴抛物线顶点坐标为（0，-2）．
本题考查了二次函数的图像和性质，掌握待定系数法求解析式和化为顶点式是解二次函数题目的关键.
19. 如图，在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC=3．
（1）以BC边上一点O为圆心作⊙O，使⊙O分别与AC、AB都相切 (要求：尺规作图，保留作图痕迹，没有写作法) ；
（2）求⊙O的面积．

【正确答案】（1）图形见解析（2）3π

【分析】（1）直接利用角平分线的作法得出∠CAB的角平分线，进而得出答案；
（2）利用勾股定理得出⊙O的半径，进而利用圆的面积求法得出答案．
【详解】解:（1）如图所示：⊙O为所求的图形．

（2）在Rt△ABC中，
∵∠ABC＝30°，
∴∠CAB＝60°，
∵AO平分∠CAB，
∴∠＝30°，
设，则，
∵在Rt△ACO中，，
∴,
解得：或（负值没有合题意，舍去），
∴⊙O的面积为．
此题主要考查了复杂作图以及勾股定理，正确掌握角平分线的性质是解题关键．
四、解 答 题（二）（本大题共3小题，每小题7分，共21分）
20. 车辆润扬大桥收费站时，4个收费通道 A．B、C、D中，可随机选择其中的一个通过．
（1）一辆车此收费站时，选择 A通道通过的概率是 ；
（2）求两辆车此收费站时，选择没有同通道通过的概率．
【正确答案】（1）；（2）．

【详解】试题分析：（1）根据概率公式即可得到结论；
（2）画出树状图即可得到结论．
试题解析：（1）选择 A通道通过的概率=，
故答案为；
（2）设两辆车为甲，乙，如图，两辆车此收费站时，会有16种可能的结果，其中选择没有同通道通过的有12种结果，∴选择没有同通道通过的概率==．

21. 某小区在绿化工程中有一块长为，宽为的矩形空地，计划在其中修建两块相同的矩形绿地，使它们的面积之和为，两块绿地之间及周边留有宽度相等的人行通道（如图所示），求人行通道的宽度．

【正确答案】人行道的宽度是．

【分析】设人行道的宽度为x米，利用平移法，可得出矩形绿地的长为(18-3x)m，宽为（6-2x）m，再根据绿地的面积=60，列方程求出符合题意的x的值，即可解答．
【详解】解：设人行道的宽度为米，根据题意得



，（没有合题意，舍去）
答：人行道的宽度是．
考查一元二次方程的应用，读懂题目，找出题目中的等量关系列出方程是解题的关键.
22. 正方形ABCD的边长为3，E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°，得到△DCM.
（1）求证：EF=FM
（2）当AE=1时，求EF的长．

【正确答案】(1)见解析；（2）.

【分析】（1）由折叠可得DE=DM，∠EDM为直角，可得出∠EDF+∠MDF=90°，由∠EDF=45°，得到∠MDF为45°，可得出∠EDF=∠MDF，再由DF=DF，利用SAS可得出三角形DEF与三角形MDF全等，由全等三角形的对应边相等可得出EF=MF；
（2）由问的全等得到AE=CM=1，正方形的边长为3，用AB-AE求出EB的长，再由BC+CM求出BM的长，设EF=MF=x，可得出BF=BM-FM=BM-EF=4-x，在直角三角形BEF中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，即为EF的长．
【详解】(1)∵△DAE逆时针旋转90°得到△DCM，
∴DE=DM ，∠EDM=90°，
∴∠EDF + ∠FDM=90°，
∵∠EDF=45°，
∴∠FDM =∠EDM=45°，
∵ DF= DF，
∴△DEF≌△DMF，
∴ EF=MF
（2） 设EF=x，
∵AE=CM=1 ，
∴ BF=BM-MF=BM-EF=4-x，
∵ EB=2，
在Rt△EBF中，由勾股定理得，
即，
解得，.
五、解 答 题（三）（本大题共3小题，每小题9分，共27分）
23. 某商场购进一批单价为4元日用品．若按每件5元的价格，每月能卖出3万件；若按每件6元的价格，每月能卖出2万件，假定每月件数y（件）与价格x（元/件）之间满足函数关系．
（1）试求y与x之间的函数关系式；
（2）当价格定为多少时，才能使每月的利润？每月的利润是多少？
【正确答案】（1）（2）当价格定为6元时，每月的利润，每月的利润为40000元

【详解】试题分析：（1）设y=kx+b，再由题目已知条件没有难得出解析式；（2）设利润为W，将W用含x的式子表示出来，W为关于x的二次函数，要求最值，将解析式化为顶点式即可求出.
试题解析：
解：（1）设y=kx+b，
根据题意得：，
解得：k=－1，b=8，
所以，y与x的函数关系式为y=－x+8；
（2）设利润为W，则W=（x－4）（－x+8）=－（x－6）2+4，
因为a=－1＜0，所以当x=6时，W为4万元.
当价格定为6元时，才能使每月的利润，每月的利润是4万元.
点睛：要求最值，一般讲二次函数解析式写成顶点式.

24. 如图⊙O是△ABC的外接圆，∠ABC＝45°，延长BC于D，连接AD，使得AD∥OC，AB交OC于E．
（1）求证：AD与⊙O相切；
（2）若AE＝2，CE＝2．求⊙O的半径和AB的长度．

【正确答案】（1）见解析；（2）AB＝．

【分析】（1）连接OA，要证明切线，只需证明OA⊥AD，根据AD∥OC，只需得到OA⊥OC，根据圆周角定理即可证明；
（2）设⊙O半径为R，则OA=R，OE=R-2，AE=2，在Rt△OAE中根据勾股定理可计算出R=4；作OH⊥AB于H，根据垂径定理得AH=BH，再利用面积法计算出OH=，然后根据勾股定理计算出AH=，再利用垂径定理得出AB=2AH═．
【详解】（1）连接OA，

∵∠ABC＝45°，
∴∠AOC＝2∠ABC＝90°，
∴OA⊥OC；
又∵AD∥OC，
∴OA⊥AD，
∴AD是⊙O的切线．
（2）设⊙O的半径为R，则OA＝R，OE＝R﹣2，AE＝2，
在Rt△OAE中，∵AO2+OE2＝AE2，
∴R2+（R﹣2）2＝（2）2，解得R＝4，
作OH⊥AB于H，如图，

OE＝OC﹣CE＝4﹣2＝2，
则AH＝BH，
∵OH•AE＝•OE•OA，
∴OH＝＝＝，
在Rt△AOH中，AH＝＝，
∵OH⊥AB，
∴AB＝2AH＝．
本题考查了切线的判定定理．综合运用了圆周角定理、等腰直角三角形的性质、等腰三角形的性质、30度的直角三角形的性质得到有关线段之间的关系，综合性较强，是中考常考体型.
25. 如图，直线l： 与x轴、y轴分别交于点B、C，B、C两点的抛物线 与x轴的另一个交点为A．

（1）求该抛物线的解析式；
（2）若点P在直线l下方的抛物线上，过点P作轴交l于点D，轴交l于点E，求的值；
（3）设F为直线l上的点，点P仍在直线l下方的抛物线上，以A、B、P、F为顶点的四边形能否构成平行四边形？若能，求出点F的坐标；若没有能，请说明理由．
【正确答案】（1）
（2）值是3 （3）能，或

【分析】（1）先确定出点B、C坐标，用待定系数法即可得出结论；
（2）先设出点P的坐标，进而得出点D、E的坐标，即可得出的函数关系式，即可得出结论；
（3）分AB为边和对角线两种情况，利用平行四边形的性质即可得出结论．
【小问1详解】
解：∵直线与x轴、y轴分别交于点B、C，
∴、，
∵点、C在抛物线解上，
∴，
解得：，
∴抛物线的解析式为．
【小问2详解】
∵点P在直线l下方的抛物线上，设，
∵轴，轴，点D，E都在直线上，
∴，，
∴，
，
∴，
即：，
∴当时，的值是3．
【小问3详解】
能，理由如下：
∵抛物线的解析式为，
令，
解得：或，
∴，，
∴，
如图，若以A、B、P、F为顶点的四边形能构成平行四边形，
当以AB为边时，则且，
设，则，
∴，
解得：或与A重合，舍去，
∴，
当以AB为对角线时，
连接交AB于点G，则，，
设，
∵，，
∴，
∴，
∴，
作于点M，于点N，则，，
设，则，
∴，
解得：或与A重合，舍去，
∴，
综上所述，以A、B、P、F为顶点的四边形能构成平行四边形，此时点F的坐标为或．

本题是二次函数综合题，主要考查了待定系数法，二次函数极值的确定方法，平行四边形的性质，二元方程组，一元二次方程，中点坐标，两点间距离公式等知识．用分类讨论的思想解决问题是解本题的关键．