2023年中考数学第一轮基础知识专题练习 专题二十一 与圆有关的计算（无答案）

专题二十一　与圆有关的计算

命题点1　　扇形的相关计算

类型一　弧长的计算

1. (2022梧州)若扇形的半径为3，圆心角为60°，则此扇形的弧长是(　　)

A. π　　　B. π　　　C. π　　　D. 2π

2. (2022云南)如图，等边△ABC的三个顶点都在⊙O上，AD是⊙O的直径．若OA＝3，则劣弧BD的长是(　　)

A.      B. π     C.      D. 2π

第2题图

3. (2022广安)如图，公园内有一个半径为18米的圆形草坪，从A地走到B地有观赏路(劣弧AB)和便民路(线段AB)．已知A、B是圆上的点，O为圆心，∠AOB＝120°，小强从A走到B，走便民路比走观赏路少走(　　)米

A. 6π－6      B. 6π－9

C. 12π－9     D. 12π－18

第3题图

4. (2022长春)如图是圆弧形状的铁轨示意图，半径OA的长度为200米，圆心角∠AOB＝90°，则这段铁轨的长度为________米．(铁轨的宽度忽略不计，结果保留π)

第4题图

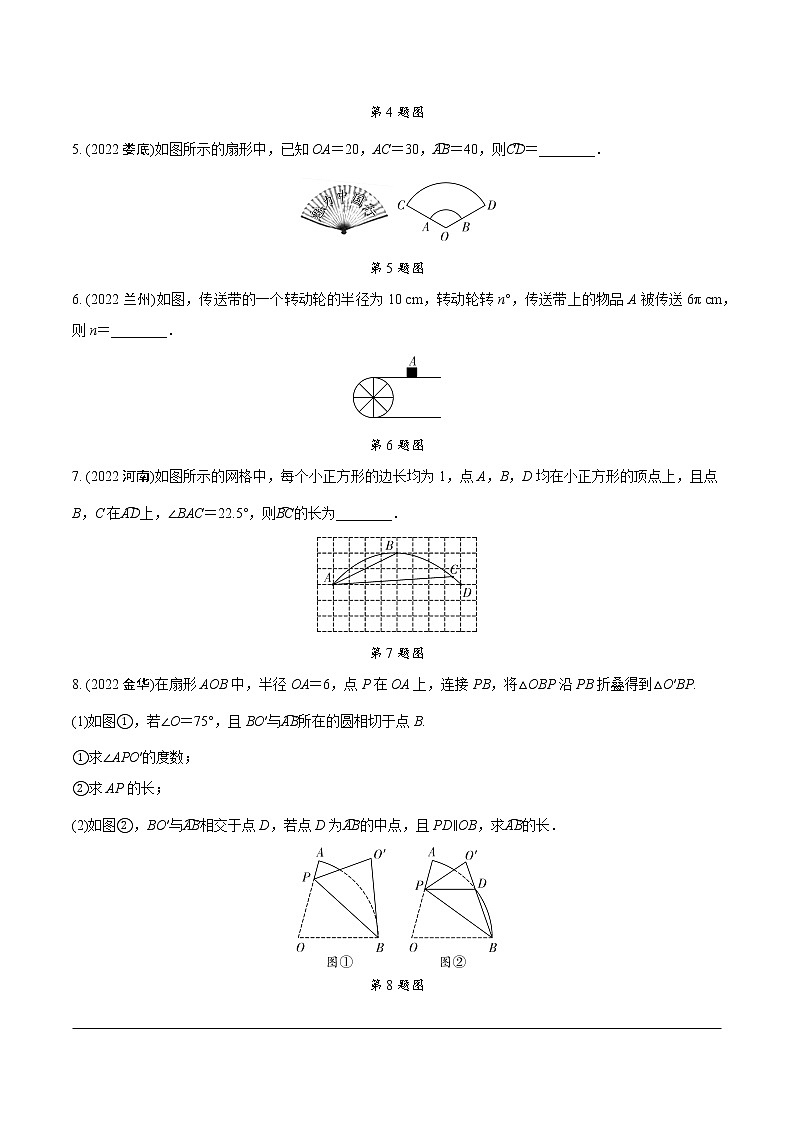
5. (2022娄底)如图所示的扇形中，已知OA＝20，AC＝30，＝40，则＝________．

第5题图

6. (2022兰州)如图，传送带的一个转动轮的半径为10 cm，转动轮转n°，传送带上的物品A被传送6π cm，则n＝________．

第6题图

7. (2022河南)如图所示的网格中，每个小正方形的边长均为1，点A，B，D均在小正方形的顶点上，且点B，C在上，∠BAC＝22.5°，则的长为________．

第7题图

8. (2022金华)在扇形AOB中，半径OA＝6，点P在OA上，连接PB，将△OBP沿PB折叠得到△O′BP.

(1)如图①，若∠O＝75°，且BO′与所在的圆相切于点B.

①求∠APO′的度数；

②求AP的长；

(2)如图②，BO′与相交于点D，若点D为的中点，且PD∥OB，求的长．

第8题图

类型二　扇形面积的计算

9. (2020福建)一个扇形的圆心角是90°，半径为4，则这个扇形的面积为________．(结果保留π)

10. (2022甘肃省卷)如图，从一块直径为4 dm的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为________dm2.

第10题图

11. (2022重庆A卷)如图，矩形ABCD的对角线AC，BD交于点O，分别以点A，C为圆心，AO长为半径画弧，分别交AB，CD于点E，F.若BD＝4，∠CAB＝36°，则图中阴影部分的面积为________．(结果保留π)

第11题图

命题点2　　与扇形有关的阴影部分面积计算

类型一　直接和差法

12. 全国视野　　新考法 (2022青海省卷)如图，一根5 m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A(羊只能在草地上活动) ，那么小羊A在草地上最大活动区域的面积是(　　)

A. π m2  　　　　　　B. π m2

C. π m2  　　　　　　D. π m2

第12题图

13. (2022怀化)如图，在⊙O中，OA＝3，∠C＝45°，则图中阴影部分的面积是________．(结果保留π)

第13题图

14. (2022广东省卷)如图，等腰直角三角形ABC中，∠A＝90°，BC＝4.分别以点B、点C为圆心，线段BC长的一半为半径作圆弧，交AB、BC、AC于点D、E、F，则图中阴影部分的面积为________．

第14题图

15. (2022宜昌)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形．如图，以边长为2厘米的等边三角形ABC的三个顶点为圆心，以边长为半径画弧，三段圆弧围成的图形就是“莱洛三角形”， 该“莱洛三角形”的面积为________平方厘米．(圆周率用π表示)

第15题图

类型二　构造和差法

16. (2022济宁)如图，在△ABC中，∠ABC＝90°，AB＝2，AC＝4，点O为BC的中点，以O为圆心，以OB为半径作半圆，交AC于点D，则图中阴影部分的面积是________．

第16题图

17. (2022资阳)如图，在矩形ABCD中，AB＝2 cm，AD＝ cm，以点B为圆心，AB长为半径画弧，交CD于点E，则图中阴影部分的面积为________cm2.

第17题图

类型三　等积转化法

18. (2022泰安)若△ABC为直角三角形，AC＝BC＝4，以BC为直径画半圆如图所示，则阴影部分的面积为________．

第18题图

19. (2020朝阳)如图，点A，B，C是⊙O上的点，连接AB，AC，BC，且∠ACB＝15°，过点O作OD∥AB交⊙O于点D，连接AD，BD，已知⊙O半径为2，则图中阴影面积为________．

第19题图

类型四　容斥原理法

20. (2022荆门)如图，正方形ABCD的边长为2，分别以B，C为圆心，以正方形的边长为半径的圆相交于点P，那么图中阴影部分的面积为________．

第20题图

命题点3　　圆切线与阴影部分求面积结合

21. (2022扬州)如图，四边形ABCD中，AD∥BC，∠BAD＝90°，CB＝CD，连接BD，以点B为圆心，BA长为半径作⊙B，交BD于点E.

(1)试判断CD与⊙B的位置关系，并说明理由；

(2)若AB＝2，∠BCD＝60°，求图中阴影部分的面积．

第21题图

22. (2022江西)如图①，四边形ABCD内接于⊙O, AD为直径，过点C作CE⊥AB于点E，连接AC.

(1)求证：∠CAD＝∠ECB；

(2)若CE是⊙O的切线，∠CAD＝30°，连接OC，如图②.

①请判断四边形ABCO的形状，并说明理由；

②当AB＝2时，求AD，AC与围成阴影部分的面积．

第22题图

命题点4　　圆锥、圆柱的相关计算

23. (2022聊城)用一块弧长16π cm的扇形铁片，做一个高为6cm的圆锥形工件侧面(接缝忽略不计)，那么这个扇形铁片的面积为________cm2.

24. (2022扬州)如图是某圆柱体果罐，它的主视图是边长为10 cm的正方形，该果罐侧面积为________cm2.

第24题图

25. 全国视野　　新考法 (2022呼和浩特)已知圆锥的母线长为10，高为8，则该圆锥的侧面展开图(扇形)的弧长为________(用含π的代数式表示)，圆心角为________度．

26. (2022黔东南州)如图，要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计)，若该圆锥的底面圆周长为20π cm，侧面积为240π cm2，则这个扇形的圆心角的度数是________度．

第26题图

27. (2022北部湾经济区)如图，从一块边长为2，∠A＝120°的菱形铁片上剪出一个扇形，这个扇形在以A为圆心的圆上(阴影部分)．且圆弧与BC，CD分别相切于点E，F，将剪下来的扇形围成一个圆锥．则圆锥的底面圆半径是________．

第27题图

28. (2022邵阳)某种冰激凌的外包装可以视为圆锥，它的底面圆直径ED与母线AD长之比为1∶2.制作这种外包装需要用如图所示的等腰三角形材料，其中AB＝AC，AD⊥BC.将扇形EAF围成圆锥时，AE，AF恰好重合．

(1)求这种加工材料的顶角∠BAC的大小；

(2)若圆锥底面圆的直径ED为5 cm，求加工材料剩余部分(图中阴影部分)的面积．(结果保留π)

第28题图

命题点5　　圆与正多边形的相关计算

29. (2022贵阳)如图，⊙O与正五边形ABCDE的两边AE，CD相切于A，C两点，则∠AOC的度数是(　　)

A. 144°　　  B. 130°　 　 C. 129°　 　 D. 108°

第29题图

30. (2022成都)如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画圆，则图中阴影部分的面积为(　　)

A. 4π    B. 6π    C. 8π    D. 12π

第30题图

31. (2022山西)如图，正六边形ABCDEF的边长为2，以A为圆心，AC的长为半径画弧，得，连接AC, AE，则图中阴影部分的面积为(　　)

A. 2π    B. 4π    C. π    D. π

第31题图

32. (2022绥化)边长为4 cm的正六边形，它的外接圆与内切圆半径的比值是________．

33. (2022大庆)如图，作⊙O的任意一条直径FC，分别以F，C为圆心，以FO的长为半径作弧，与⊙O相交于点E，A和D，B，顺次连接AB，BC，CD，DE，EF，FA，得到六边形ABCDEF.则⊙O的面积与阴影区域面积的比值为________．

第33题图

34. (2022河北)如图，⊙O的半径为6，将该圆周12等分后得到表盘模型，其中整钟点为An(n为1～12的整数)，过点A7作⊙O的切线交A1A11延长线于点P.

(1)通过计算比较直径和劣弧A7A11长度哪个更长；

(2)连接A7A11，则A7A11和PA1有什么特殊位置关系？请简要说明理由；

(3)求切线长PA7的值．

第34题图