2023年中考数学第一轮基础知识专题练习 专题十七 平行四边形与多边形（无答案）

专题十七　平行四边形与多边形

命题点1　　平行四边形的判定

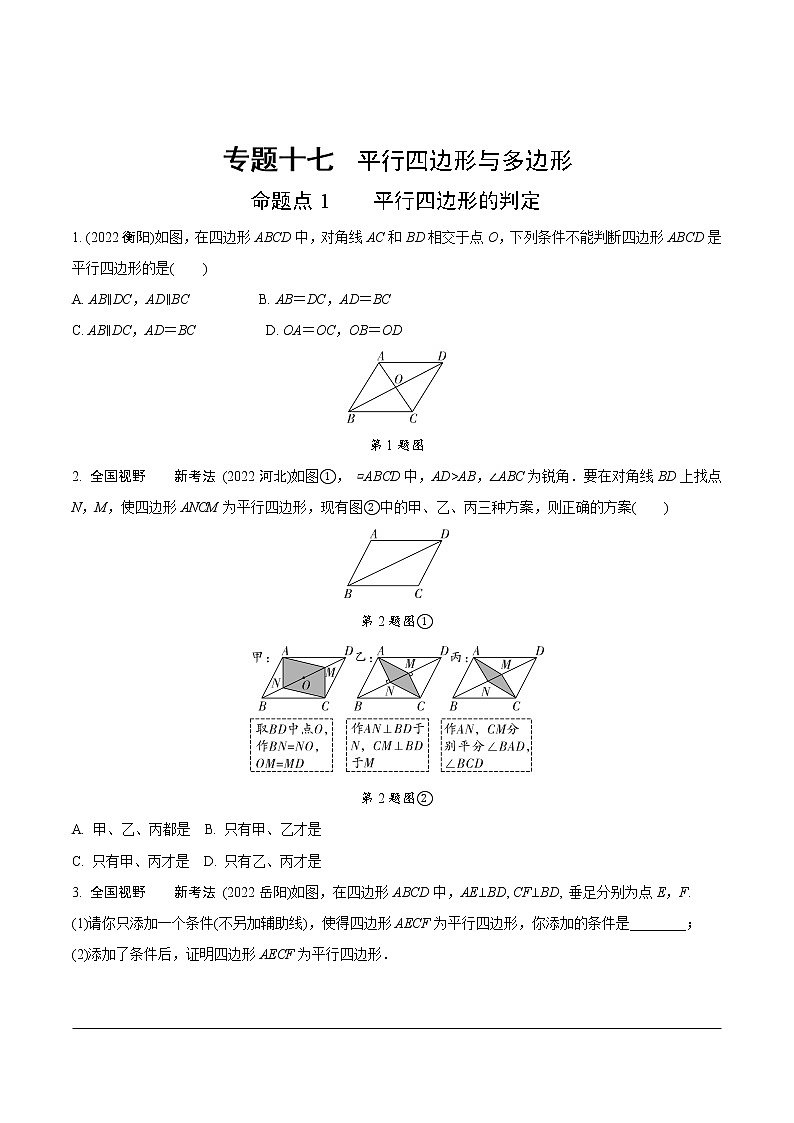
1. (2022衡阳)如图，在四边形ABCD中，对角线AC和BD相交于点O，下列条件不能判断四边形ABCD是平行四边形的是(　　)

A. AB∥DC，AD∥BC　　　　　B. AB＝DC，AD＝BC

C. AB∥DC，AD＝BC　　　　　D. OA＝OC，OB＝OD

第1题图

2. 全国视野　　新考法 (2022河北)如图①， ▱ABCD中，AD>AB，∠ABC为锐角．要在对角线BD上找点N，M，使四边形ANCM为平行四边形，现有图②中的甲、乙、丙三种方案，则正确的方案(　　)

第2题图①

第2题图②

A. 甲、乙、丙都是  B. 只有甲、乙才是

C. 只有甲、丙才是  D. 只有乙、丙才是

3. 全国视野　　新考法 (2022岳阳)如图，在四边形ABCD中，AE⊥BD, CF⊥BD, 垂足分别为点E，F.

(1)请你只添加一个条件(不另加辅助线)，使得四边形AECF为平行四边形，你添加的条件是________；

(2)添加了条件后，证明四边形AECF为平行四边形．

第3题图

4. (2022北京)如图，在四边形ABCD中，∠ACB＝∠CAD＝90°，点E在BC上，AE∥DC，EF⊥AB，垂足为F.

(1)求证：四边形AECD是平行四边形；

(2)若AE平分∠BAC，BE＝5，cosB＝，求BF和AD的长．

第4题图

5. (2022聊城)如图，在四边形ABCD中，AC与BD相交于点O，且AO＝CO，点E在BD上，满足∠EAO＝∠DCO.

(1)求证：四边形AECD是平行四边形；

(2)若AB＝BC，CD＝5，AC＝8，求四边形AECD的面积．

第5题图

命题点2　　平行四边形性质的相关证明与计算

6. (2022株洲)如图所示，四边形ABCD是平行四边形，点E在线段BC的延长线上，若∠DCE＝132°，则∠A＝(　　)

第6题图

A. 38° 

B. 48° 

C. 58° 

D. 66°

7. (2022宜宾)下列说法正确的是(　　)

A. 平行四边形是轴对称图形

B. 平行四边形的邻边相等

C. 平行四边形的对角线互相垂直

D. 平行四边形的对角线互相平分

8. (2022荆门)如图，将一副三角板在平行四边形ABCD中作如下摆放，设∠1＝30°，那么∠2＝(　　)

A. 55°　　　B. 65°　　　C. 75°　　　D. 85°

第8题图

9. (2022益阳)如图，▱ABCD的对角线AC，BD交于点O，若AC＝6，BD＝8，则AB的长可能是(　　)

A. 10    B. 8    C. 7    D. 6

10. (2022南充)如图，点O是▱ABCD对角线的交点，EF过点O分别交AD，BC于点E，F，下列结论成立的是(　　)

A. OE＝OF           B. AE＝BF 

C. ∠DOC＝∠OCD    D. ∠CFE＝∠DEF

第10题图

11. (2022天津)如图，▱ABCD的顶点A，B，C的坐标分别是(0，1)，(－2，－2)，(2，－2)，则顶点D的坐标是(　　)

A. (－4，1)  B. (4，－2)

C. (4，1)    D. (2，1)

第11题图

12. (2022陕西)如图，在▱ABCD中，AB＝5，BC＝8，E是边BC的中点，F是▱ABCD内一点，且∠BFC＝90°.连接AF并延长，交CD于点G.若EF∥AB，则DG的长为(　　)

A.      B.      C. 3     D. 2

第12题图

13. (2022贵阳)如图，在▱ABCD中，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，若AB＝3，AD＝4，则EF的长是(　　)

A. 1      B. 2      C. 2.5      D. 3

第13题图

14. (2022泰安)如图，在平行四边形ABCD中，E是BD的中点．则下列四个结论：

①AM＝CN；

②若MD＝AM，∠A＝90°，则BM＝CM；

③若MD＝2AM，则S△MNC＝S△BNE；

④若AB＝MN，则△MFN与△DFC全等．

其中正确结论的个数为(　　)

A. 1个　　　B. 2个　　　C. 3个　　　D. 4个

第14题图

15. (2022湘潭)如图，在▱ABCD中，对角线AC，BD相交于点O，点E是边AB的中点．已知BC＝10，则OE＝________．

第15题图

16. (2022扬州)如图，在▱ABCD中，点E在AD上，且EC平分∠BED，若∠EBC＝30°，BE＝10，则▱ABCD的面积为________．

第16题图

17. (2022嘉兴)如图，在▱ABCD中，对角线AC，BD交于点O，AB⊥AC，AH⊥BD于点H，若AB＝2，BC＝2，则AH的长为________．

第17题图

18. (2022青海省卷)如图，在▱ABCD中，对角线BD＝8 cm，AE⊥BD，垂足为E，且AE＝3 cm, BC＝4 cm.则AD与BC之间的距离为________．

第18题图

19. (2022陕西)如图，在四边形ABCD中，AD∥BC，∠B＝∠C.E是边BC上一点，且DE＝DC.求证：AD＝BE.

第19题图

20. (2022桂林)如图，在平行四边形ABCD中，点O是对角线BD的中点，EF过点O，交AB于点E，交CD于点F.

(1)求证：∠1＝∠2；

(2)求证：△DOF≌△BOE.

第20题图

21. 全国视野　　新考法 (2022宿迁)在①AE＝CF；②OE＝OF；③BE∥DF这三个条件中任选一个补充在下面横线上，并完成证明过程．

已知：如图，四边形ABCD是平行四边形，对角线AC、BD相交于点O，点E、F在AC上，________(填写序号)．

求证：BE＝DF.

注：如果选择多个条件分别解答，按第一个解答计分．

第21题图

22. (2022怀化)已知：如图，四边形ABCD为平行四边形，点E、A、C、F在同一直线上，AE＝CF.

求证：(1)△ADE≌△CBF；

(2)ED∥BF.

第22题图

23. (2022乐山)点P是平行四边形ABCD的对角线AC所在直线上的一个动点(点P不与点A、C重合)，分别过点A、C向直线BP作垂线，垂足分别为点E、F.点O为AC的中点．

(1)如图①，当点P与点O重合时，线段OE和OF的关系是________；

(2)当点P运动到如图②所示的位置时，请在图中补全图形并通过证明判断(1)中的结论是否仍然成立？

(3)如图③，点P在线段OA的延长线上运动，当∠OEF＝30°时，试探究线段CF，AE，OE之间的关系．

第23题图

命题点3　　多边形及其性质

类型一　多边形的计算

24. (2022云南)一个10边形的内角和等于(　　)

A. 1800°　　　　B. 1660°

C. 1440°        D. 1200°

25. (2022北京)下列多边形中，内角和最大的是(　　)

26. (2022扬州)如图，点A、B、C、D、E在同一平面内，连接AB、BC、CD、DE、EA，若∠BCD＝100°，则∠A＋∠B＋∠D＋∠E＝(　　)

第26题图

A. 220°    B. 240° 

C. 260°    D. 280°

27. (2022新疆)四边形的外角和等于________°.

28. (2022广安)一个多边形的内角和是外角和的3倍，则这个多边形的边数是________．

29. (2022金华)一个多边形过顶点剪去一个角后，所得多边形的内角和为720°，则原多边形的边数是________．

类型二　正多边形的性质及计算

30. (2022连云港)正五边形的内角和是(　　)

A. 360°　　　B. 540°　　　C. 720°　　　D. 900°

31. (2022眉山)正八边形中，每个内角与每个外角的度数之比为(　　)

A. 1∶3  B. 1∶2  C. 2∶1  D. 3∶1

32. (2022营口)如图，一束太阳光线平行照射在放置于地面的正六边形上．若∠1＝19°，则∠2的度数为(　　)

A. 41°  B. 51° 

C. 42°  D. 49°

第32题图

33. (2022福建)如图，点F在正五边形ABCDE的内部，△ABF为等边三角形，则∠AFC等于(　　)

A. 108°  B. 120° 

C. 126°  D. 132°

第33题图

34. (2022株洲)如图所示，在正六边形ABCDEF内，以AB为边作正五边形ABGHI，则∠FAI＝(　　)

第34题图

A．10°　 　B. 12°　 　C. 14°　 　D. 15°

35. (2022河北)如图，点O为正六边形ABCDEF对角线FD上一点，S△AFO＝8，S△CDO＝2, 则S正六边形ABCDEF的值是(　　)

A. 20　　　　B. 30

C. 40        D. 随点O位置而变化

第35题图　　

36. (2022衢州)如图，在正五边形ABCDE中，连接AC，BD交于点F，则∠AFB的度数为________．

第36题图

37. (2022湖州)为庆祝中国共产党建党100周年，某校用红色灯带制作了一个如图所示的正五角星(A，B，C，D，E是正五边形的五个顶点)，则图中∠A的度数是______度．

第37题图

38. (2022上海)六个带30度角的直角三角板拼成一个正六边形，直角三角板的最短边为1，求中间正六边形的面积________．

第38题图

类型三　平面镶嵌

39. (2022铜仁)用形状，大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌．工人师傅不能用下列哪种形状、大小完全相同的一种地砖在平整的地面上镶嵌(　　)

A. 等边三角形     B. 正方形     C. 正五边形   D. 正六边形