2022-2023学年浙江省湖州市九年级上册数学期末专项突破模拟题（AB卷）含解析

这是一份2022-2023学年浙江省湖州市九年级上册数学期末专项突破模拟题（AB卷）含解析，共50页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年浙江省湖州市九年级上册数学期末专项突破模拟题（A卷）
一、选一选（本题有10小题，每小题3分，共30分）
1. 如图，Rt△ABC中，∠C=90°，AB=7，∠B=35°，则AC的长为（ ）

A. 7cos35° B. 7tan35° C. 7sin35° D. 7sin55°
2. 若，则（ ）
A B. C. D.
3. 抛物线y=2(x+4)2-3的对称轴是 ( )
A. 直线x=4 B. 直线x=－4 C. 直线x=3 D. 直线x=－3
4. 若的每条边长增加各自的得,则的度数与其对应角的度数相比（ ）
A. 增加了 B. 减少了 C. 增加了 D. 没有改变
5. 如图，AB是⊙O的直径，C是⊙O上的一点，OD⊥BC于点D，AC=8，则OD的长为( )

A. 3 B. 4 C. 4.5 D. 5
6. 如图，在△ABC中，DE∥BC，且，则下列结论没有正确的是（　　）

A. B. C. D.
7. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则劣弧AC的长（　　）

A. 8 B. 4 C. 2π D. π
8. 已知二次函数的与的部分对应值如下表：

…
-1
0
1
3
…

…
-3
1
3
1
…
则下列判断中正确的是（ ）
A. 抛物线开口向上 B. 抛物线与轴的交点在轴负半轴上
C. 当时， D. 方程的正根在3与4之间
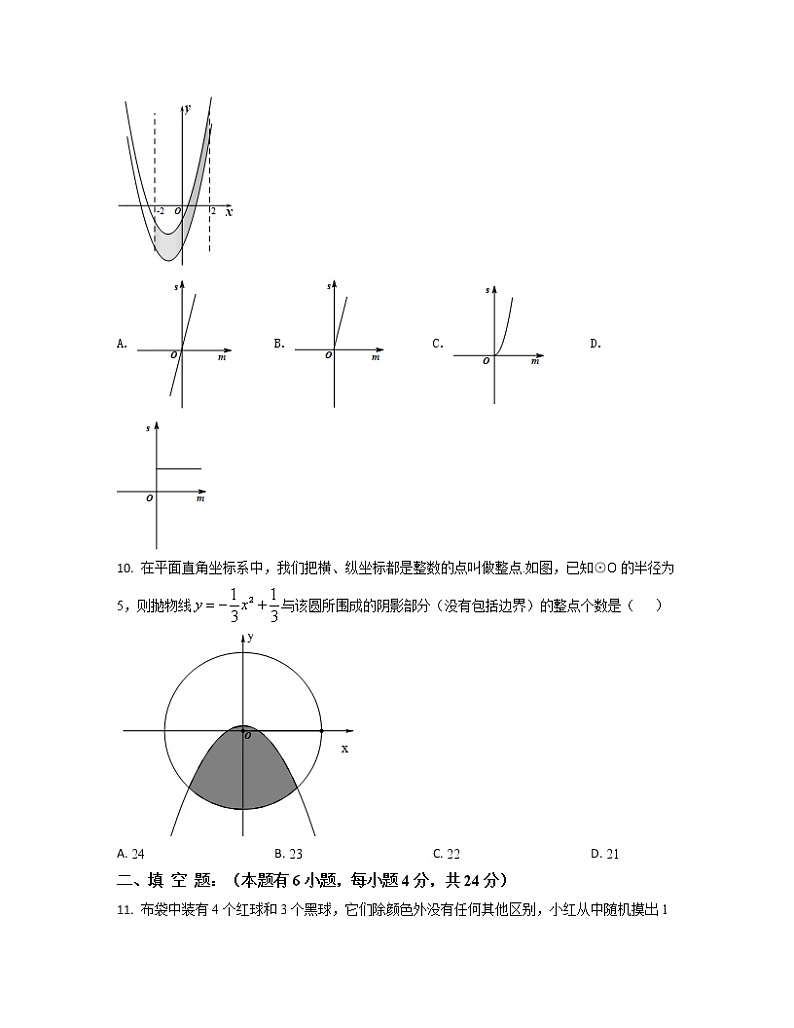
9. 如图，已知抛物线y=x2+3x-4，把此抛物线沿y轴向上平移，平移后抛物线和原抛物线与点(-2，0)，（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m,则下列图象中，能表示s与m的函数关系的图象大致是（　　）

A. B. C. D.
10. 在平面直角坐标系中，我们把横、纵坐标都是整数的点叫做整点.如图，已知⊙O的半径为5，则抛物线与该圆所围成的阴影部分（没有包括边界）的整点个数是（ ）

A. 24 B. 23 C. 22 D. 21
二、填 空 题：（本题有6小题，每小题4分，共24分）
11. 布袋中装有4个红球和3个黑球，它们除颜色外没有任何其他区别，小红从中随机摸出1个球，摸出红球的概率是________ ．
12. 若线段c是线段a，b的比例中项，且，，则_____________．
13. 如图，在Rt△ABC中，∠A=60°，AB=1，将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置，点A1刚好落在BC的延长线上，求点A从开始到结束所的路径长为（结果保留π）______．

14. 如图，在⊙O中，是⊙O的直径，，点是点关于的对称点，是上的一动点，下列结论：①；②；③；④的最小值是10．上述结论中正确的个数是_________．

15. 一个长方体木箱沿斜面下滑，当木箱滑至如图所示位置时，AB=3m，已知木箱高BD=1m，斜面坡角为30°，则木箱端点D距地面AC的高度为________．

16. 如图1，点D为直角三角形ABC的斜边AB上的中点，DE⊥AB交AC于E, 连EB、CD，线段CD与BF交于点F.若tanA=,则=_____.如图2，点D为直角三角形ABC的斜边AB上的一点，DE⊥AB交AC于E, 连EB、CD；线段CD与BF交于点F.若，tanA=，则=____.

三、解 答 题：（本题有8个小题，共66分）
17. 计算：
18. 如图所示，点D在△ABC的AB边上，AD=2，BD=4，AC=2．求证：△ACD∽△ABC．

19. 2017年11月11日，张杰参加了某网点“翻牌抽奖”.如图所示，4张牌上分别写有对应的为10元，15元，20元和“谢谢惠顾”的字样.
⑴如果随机翻1张牌，那么抽中有奖的概率为 ，抽中15元及以上的概率为 .
⑵如果随机翻2张牌，且次翻过的牌没有再参加下次翻牌，用画树状图或列表法列出抽奖的所有等可能性情况，并求出获总值没有低于30元的概率.

20. 小鹏学完解直角三角形知识后，给同桌小艳出了一道题：“如图所示，把一张长方形卡片ABCD放在每格宽度都为6mm的横格纸中，恰好四个顶点都在横格线上，已知a=36°，求长方形卡片的周长．”请你帮小艳解答这道题．（到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）

21. 如图，已知点O为半圆的圆心，直径AB=12，C是半圆上一点，OD⊥AC于点D，OD=3．
（1）求AC的长；
（2）求图中阴影部分的面积.

22. 元旦前夕，湖州吴兴某工艺厂设计了一款成本10元/件的工艺品投放市场试销.试销发现，每天量y（件）与单价x（元/件）之间的关系可近似地看作函数：y=-10x+700. （利润=总价-成本总价）
⑴ 如果该厂想要每天获得5000元的利润，那么单价应定为多少元/件？
⑵ 当单价定为多少时，工艺厂试销该工艺品每天获得利润？利润是多少？
⑶ 湖州市物价部门规定，该工艺品单价没有能超过38元/件，那么单价定为多少时，工艺厂试销该工艺品每天获得的利润？
23. 某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=2米，BC=1米；上部△CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑其形状变化的三角通风窗（阴影部分均没有通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆．
（1）当MN和AB之间的距离为0.5米时，求此时△EMN的面积；
（2）设MN与AB之间的距离为x 米，试将△EMN的面积S（平方米）表示成关于x的函数；
（3）请你探究△EMN的面积S（平方米）有无值，若有，请求出这个值；若没有，请说明理由．

24. 如图，在平面直角坐标系中，抛物线试纸y=ax2+bx+c与x轴交于点A,C，与y轴交于点B.已知点A坐标为(8，0)，点B为(0，8)，点D为（0，3），tan∠DCO=，直线AB和直线CD相交于点E.
⑴ 求抛物线的解析式，并化成y=a(x-m)2+h的形式；
⑵ 设抛物线顶点为G，请在直线AB上方的抛物线上求点P的坐标，使得S△ABP=S△ABG.
⑶ 点M为直线AB上的一点，过点M作x轴的平行线分别交直线AB，CD于点M，N，连结DM，DN，是否存在点M，使得△DMN为等腰三角形？若存在，请求出点M的坐标；若没有存在，请说明理由.











2022-2023学年浙江省湖州市九年级上册数学期末专项突破模拟题（A卷）
一、选一选（本题有10小题，每小题3分，共30分）
1. 如图，Rt△ABC中，∠C=90°，AB=7，∠B=35°，则AC的长为（ ）

A. 7cos35° B. 7tan35° C. 7sin35° D. 7sin55°
【正确答案】C

【分析】在直角三角形中，根据角的正弦值与边的关系，可求出AC的长.
【详解】∵在Rt△ABC中, ∠C=90°，
∴sin∠B=，即AC=AB sin∠B，
∵∠B=35°，AB=7，
∴AC=7sin35°.
故选：C.
本题考查了解直角三角形中三角函数的应用，熟练掌握直角三角形边角之间的关系是解题的关键.
2. 若，则（ ）
A. B. C. D.
【正确答案】A

【详解】试题分析：∵
∴
∴
故选A.
考点：分式的值.
3. 抛物线y=2(x+4)2-3的对称轴是 ( )
A. 直线x=4 B. 直线x=－4 C. 直线x=3 D. 直线x=－3
【正确答案】B

【详解】抛物线的顶点式方程为y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，所以抛物线y=2（x+4）2-3的对称轴是x=-4；
故选B．
4. 若的每条边长增加各自的得,则的度数与其对应角的度数相比（ ）
A. 增加了 B. 减少了 C. 增加了 D. 没有改变
【正确答案】D

【分析】根据两个三角形三边对应成比例，这两个三角形相似判断出两个三角形相似，再根据相似三角形对应角相等解答.
【详解】∵△ABC的每条边长增加各自的10%得，
∴△ABC与的三边对应成比例，
∴△ABC∽△
∴∠=∠B.
故选D.
本题考察了相似三角形性质的应用，解决本题的关键是确定两三角形相似.
5. 如图，AB是⊙O直径，C是⊙O上的一点，OD⊥BC于点D，AC=8，则OD的长为( )

A. 3 B. 4 C. 4.5 D. 5
【正确答案】B

【详解】∴CD=BD，
∵OA=OB，AC=8，
∴OD=AC=4.
故选B.
6. 如图，在△ABC中，DE∥BC，且，则下列结论没有正确的是（　　）

A. B. C. D.
【正确答案】C

【详解】∵，DE∥BC，
∴,A、B均正确；
∴△ADE∽△ABC，
∴,C错误；
∴，，正确.
故选：C.
7. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为4，∠B=135°，则劣弧AC的长（　　）

A. 8 B. 4 C. 2π D. π
【正确答案】C

【详解】连接OA、OC，如图：

∵∠B=135°，
∴∠D=180°−135°=45°，
∴∠AOC=90°，
则弧AC的长==2π.
故选C.
8. 已知二次函数的与的部分对应值如下表：

…
-1
0
1
3
…

…
-3
1
3
1
…
则下列判断中正确的是（ ）
A. 抛物线开口向上 B. 抛物线与轴的交点在轴负半轴上
C. 当时， D. 方程的正根在3与4之间
【正确答案】D

【分析】根据题意和表格中的数据可以得到该函数的对称轴、开口方向，从而可以判断各个选项中的说法是否正确，从而可以解答本题．
【详解】解：由图表可得，
该函数的对称轴是直线x=，有值，
∴抛物线开口向下，故选项A错误，
抛物线与y轴的交点为（0，1），故选项B错误，
x=-1和x=4时的函数值相等，则x=4时，y=-3＜0，故选项C错误，
x=3时，y=1，x=4时，y=-3，方程ax2+bx+c=0的正根在3与4之间，故选项D正确，
故选：D．
本题考查抛物线与x轴的交点、二次函数的性质，解答本题的关键是明确题意，找出所求问题需要的条件，利用二次函数的性质解答．
9. 如图，已知抛物线y=x2+3x-4，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线与点(-2，0)，（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m,则下列图象中，能表示s与m的函数关系的图象大致是（　　）

A. B. C. D.
【正确答案】B

【详解】试题解析：如图，

我们把抛物线沿y轴向上平移，平移后的抛物线和原抛物线及直线x=2，x=-2所围成的阴影部分的面积S可以看做和矩形BB′C′C等积，于是可以看出S与m是正比例函数关系
故选B．
考点：函数图象与几何变换.
10. 在平面直角坐标系中，我们把横、纵坐标都是整数的点叫做整点.如图，已知⊙O的半径为5，则抛物线与该圆所围成的阴影部分（没有包括边界）的整点个数是（ ）

A. 24 B. 23 C. 22 D. 21
【正确答案】D

【详解】∵抛物线顶点坐标为（0，），
半径为5的⊙O与y轴负半轴交点为（0，-5），
∴当y=0时，x=±1，∴整点（1，0），（0，0），（-1，0）；
当y=-1，x=±2，∴整点为（2，-1），（-1，-1），（0，-1），（1，-1），（2，-1）；
当y=-2，x=±，∴整点（2，-2），（-1，-2），（0，-2），（1，-2），（2，-2）；
当y=-3，x=±，∴整点为（3，-3），（2，-3），（1，-3），（0，-3），（-1，-3），（-2，-3），（-3，-3）；
当y=-4，x=±，∴整点为（3，-4），（2，-4），（1，-4），（0，-4），（-1，-4），（-2，-4），（-3，-4）；
当y=-5，x=±4，∴整点为（4，-5），（3，-5），（2，-5），（1，-5），（0，-5），（-1，-5），（-2，-5），（-3，-5），（4，-5）；
所以在阴影部分（没有包括边界）的整点为：（0，0），（-1，-1），（0，-1），（1，-1），（-1，-2），（0，-2），（1，-2），（3，-3），（2，-3），（1，-3），（0，-3），（-1，-3），（-2，-3），（-3，-3），（3，-4），（2，-4），（1，-4），（0，-4），（-1，-4），（-2，-4），（-3，-4），故整点为21个.
故选D.
点睛：本题考查了二次函数图象上点的坐标特征，解题是关键是二次函数和圆的图象找出整点的坐标，注意没有包含边界点这一条件.
二、填 空 题：（本题有6小题，每小题4分，共24分）
11. 布袋中装有4个红球和3个黑球，它们除颜色外没有任何其他区别，小红从中随机摸出1个球，摸出红球的概率是________ ．
【正确答案】

【详解】∵有4个红球3个黑球，
∴球的总数=4+3=7，
∴随机摸出一个球,摸到红球的概率=.
故答案为.
12. 若线段c是线段a，b的比例中项，且，，则_____________．
【正确答案】6

【分析】根据比例中项的定义可得c2=ab，从而易求c．
【详解】解：∵线段c是线段a，b的比例中项，
∴c2=ab，
∵a=4，b=9，
∴c2=36，
∴c=6（负数舍去），
故答案是：6．
本题考查了比例线段，解题的关键是理解比例中项的含义．
13. 如图，在Rt△ABC中，∠A=60°，AB=1，将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置，点A1刚好落在BC的延长线上，求点A从开始到结束所的路径长为（结果保留π）______．

【正确答案】．

【详解】在Rt△ABC中，∠A=60°，可得AC==2，∠ACB=30°，因此求得∠ACA1=150°，所以点A从开始到结束所的路径长为以C为圆心、2为半径的弧，即=，
故答案为 ．
点睛：本题考查的是点的轨迹以及弧长的计算，利用余弦的概念求出AC=2，根据弧长公式计算求出点A从开始到结束所的路径长即可．
14. 如图，在⊙O中，是⊙O的直径，，点是点关于的对称点，是上的一动点，下列结论：①；②；③；④的最小值是10．上述结论中正确的个数是_________．

【正确答案】3

【分析】①根据点是点关于的对称点可知，进而可得；
②根据一条弧所对的圆周角等于圆心角的一半即可得结论；
③根据等弧对等角，可知只有当和重合时，，；
④作点关于的对称点，连接，DF，此时的值最短，等于的长，然后证明DF是的直径即可得到结论．
【详解】解：，点是点关于的对称点，
，
，①正确；，∴②正确；
的度数是60°，
的度数是120°，
∴只有当和重合时，，

∴只有和重合时，，③错误；
作关于的对称点，连接，交于点，连接交于点，此时的值最短，等于的长．
连接，并且弧的度数都是60°，


是的直径，即，
∴当点与点重合时，的值最小，最小值是10，∴④正确．
故3．

本题考查了圆的综合知识，涉及圆周角、圆心角、弧、弦的关系、最短距离的确定等，掌握圆的基本性质并灵活运用是解题关键．
15. 一个长方体木箱沿斜面下滑，当木箱滑至如图所示位置时，AB=3m，已知木箱高BD=1m，斜面坡角为30°，则木箱端点D距地面AC的高度为________．

【正确答案】

【详解】连接AD，

∵∠A=30°，
∴∠BOD=∠AOE=60°，
则OD==，OB==，
∴OA=AB−OB=3-，
则OE=OA=-，
∴DE=OD+OE=m，
故m.
16. 如图1，点D为直角三角形ABC的斜边AB上的中点，DE⊥AB交AC于E, 连EB、CD，线段CD与BF交于点F.若tanA=,则=_____.如图2，点D为直角三角形ABC的斜边AB上的一点，DE⊥AB交AC于E, 连EB、CD；线段CD与BF交于点F.若，tanA=，则=____.

【正确答案】 ①. ②.

【详解】
设AC=8a，∵DE⊥AB，tanA═，
∴DE=AD，
∵Rt△ABC中,AC═a，,tanA═，
∴BC=,AB==，
又∵△AED沿DE翻折，A恰好与B重合，
∴AD=BD=,DE=，
∴Rt△ADE中,AE==，
∴CE=8a-5a=3a，
∴Rt△BCE中,BE==5a，
如图，过点C作CG⊥BE于G，作DH⊥BE于H，则
Rt△BDE中,DH==2a，
Rt△BCE中,CG==，
∵CG∥DH，
∴△CFG∽△DFH，
∴，
故答案为6：5.
（2）若，tanA=，
∴AD=, BD=，DE=，
∴Rt△ADE中,AE==，
∴CE=8a-=，
∴Rt△BCE中,BE==，
如图，过点C作CG⊥BE于G，作DH⊥BE于H，则
Rt△BDE中,DH==，
Rt△BCE中,CG==，
∵CG∥DH，
∴△CFG∽△DFH，
∴，
故答案为44：15.
点睛：此题考查了勾股定理、正切、三角形的面积、相似三角形的判定与性质等知识，解题的关键是作出辅助线构造出直角三角形的高以及相似三角形，利用相似三角形的对应边成比例来解决问题.
三、解 答 题：（本题有8个小题，共66分）
17. 计算：
【正确答案】

【详解】试题分析：根据二次根式的化简、角的三角函数值计算合并即可.
试题解析：===.
18. 如图所示，点D在△ABC的AB边上，AD=2，BD=4，AC=2．求证：△ACD∽△ABC．

【正确答案】证明见解析.

【详解】试题分析：首先利用已知得出=，进而利用相似三角形的判定方法得出即可．
试题解析：∵，
，
∴ ，
又∵∠A=∠A，
∴△ABC∽△ACD.
19. 2017年11月11日，张杰参加了某网点的“翻牌抽奖”.如图所示，4张牌上分别写有对应的为10元，15元，20元和“谢谢惠顾”的字样.
⑴如果随机翻1张牌，那么抽中有奖的概率为 ，抽中15元及以上的概率为 .
⑵如果随机翻2张牌，且次翻过的牌没有再参加下次翻牌，用画树状图或列表法列出抽奖的所有等可能性情况，并求出获总值没有低于30元的概率.

【正确答案】（1）；；（2）.

【详解】试题分析：（1）随机A的概率P（A）=A可能出现的结果数÷所有可能出现的结果数，据此计算，求出抽中有奖和15元以上的概率为多少即可；
（2）首先应用树状图法，列举出随机翻2张牌，所获的总值一共有多少种情况；然后用所获总值没有低于30元的情况的数量除以所有情况的数量，求出所获总值没有低于30元的概率为多少即可．
解：（1）3÷4=，1÷2=，
∴抽中奖的概率为，抽中15元及以上的概率为；
故答案为；；
（2） 画出树状图得：

∴由树状图可知，一共有12种等可能性的抽奖结果；其中总值没有低于30元的有4种情况. 所获总值没有低于30元的概率==.
20. 小鹏学完解直角三角形知识后，给同桌小艳出了一道题：“如图所示，把一张长方形卡片ABCD放在每格宽度都为6mm的横格纸中，恰好四个顶点都在横格线上，已知a=36°，求长方形卡片的周长．”请你帮小艳解答这道题．（到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）

【正确答案】100mm.

【详解】试题分析：作BE⊥l于点E，DF⊥l于点F，求∠ADF的度数，在Rt△ABE中，可以求得AB的值，在Rt△ADF中，可以求得AD的值，即可计算矩形ABCD的周长，即可解题．
试题解析：作BE⊥m于点，DF⊥m于点．




根据题意，得 BE=12mm， DF=24mm.
在Rt中，sin，
mm，
在Rt中，cos，
mm．
矩形的周长=2（20+30）=100mm．
21. 如图，已知点O为半圆的圆心，直径AB=12，C是半圆上一点，OD⊥AC于点D，OD=3．
（1）求AC的长；
（2）求图中阴影部分的面积.

【正确答案】（1）；（2）.

【详解】（1）∵OD⊥AC，
∴，
∴AC=2AD= ，
（2）连OC，

在Rt△ ADO中，OD=3，OA=6，
∴OD=AO，
∴∠=30° ，
又∵OA=OC，
∴∠OCA = ∠ =30°，
∴∠AOC=120° ，
∴=.
22. 元旦前夕，湖州吴兴某工艺厂设计了一款成本10元/件的工艺品投放市场试销.试销发现，每天量y（件）与单价x（元/件）之间的关系可近似地看作函数：y=-10x+700. （利润=总价-成本总价）
⑴ 如果该厂想要每天获得5000元的利润，那么单价应定为多少元/件？
⑵ 当单价定为多少时，工艺厂试销该工艺品每天获得的利润？利润是多少？
⑶ 湖州市物价部门规定，该工艺品单价没有能超过38元/件，那么单价定为多少时，工艺厂试销该工艺品每天获得的利润？
【正确答案】(1) 单价为20元/件或60元/件；（2）单价定为38元..

【详解】试题分析：（1）根据利润=总价-成本总价，得出函数关系式W=（x-10）（-10x+700），令w=5000，解得x值即可；
（2）根据利润=总价-成本总价，由（1）中函数关系式得出W=（x-10）（-10x+700），进而利用二次函数最值求法得出即可；
（3）利用二次函数的增减性，对称轴即可得出答案．
（1）由题意，得，
解得
∴单价为20元/件或60元/件；
（2）设每天的利润为W元，
则w= =，∴，此时W有值为9000，
∴当单价定为40元时，利润有值为9000元；
（3）∵k=-10