2022-2023学年河北省保定市九年级上册数学期末专项突破模拟题（AB卷）含解析

这是一份2022-2023学年河北省保定市九年级上册数学期末专项突破模拟题（AB卷）含解析，共49页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。

2022-2023学年河北省保定市九年级上册数学期末专项突破模拟题（A卷）
一、选一选（每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求）
1 若，则等于（　　）
A. B. C. D.
2. 对于二次函数，下列说法没有正确的是（　　）
A. 有最小值–3 B. 对称轴是直线x = 4
C. 顶点是（4，–3） D. 在对称轴的左侧y随x的增大而增大
3. 由6个大小相同正方体搭成的几何体如图所示，则关于它的视图说确的是（　　）

A. 正视图的面积 B. 左视图的面积
C. 俯视图的面积 D. 三个视图的面积一样大
4. 在Rt△ABC中，∠C=90°，AC=3，AB=5，那么的值是（　　）
A. B. C. D.
5. 已知圆锥的母线长为5，底面半径为3，则圆锥的表面积为（　　）
A. 15π B. 24π C. 30π D. 39π
6. 如图所示把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点，把平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的正三角形，那么剪出的正三角形全部展开铺平后得到的平面图形一定是（　　）

A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
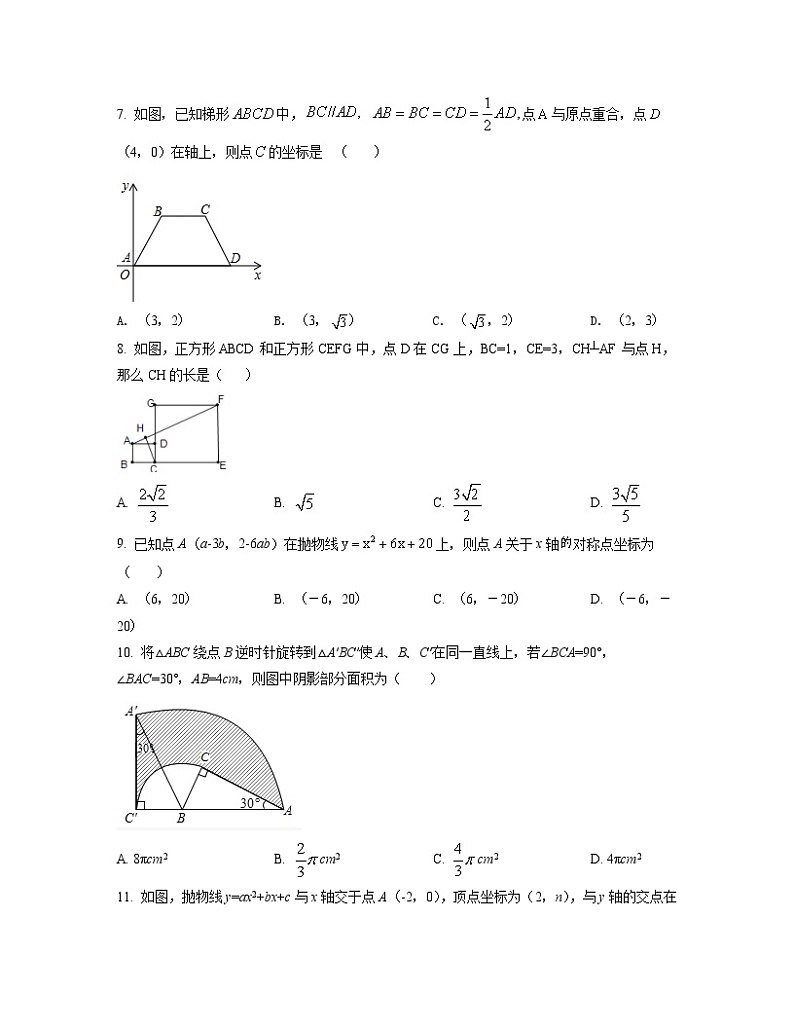
7. 如图，已知梯形中， 点与原点重合，点（4，0）在轴上，则点的坐标是 （　　）

A. （3，2） B. （3，） C. （，2） D. （2，3）
8. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，CH┴AF与点H，那么CH的长是（ ）

A. B. C. D.
9. 已知点A（a-3b，2-6ab）在抛物线上，则点A关于x轴对称点坐标为（　　）
A. （6，20） B. （－6，20） C. （6，－20） D. （－6，－20）
10. 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上，若∠BCA=90°，∠BAC=30°，AB=4cm，则图中阴影部分面积为（　　）

A. 8πcm2 B. cm2 C. cm2 D. 4πcm2
11. 如图，抛物线y=ax2+bx+c与x轴交于点A（-2，0），顶点坐标为（2，n），与y轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①当x＞6时，y＜0；②5a+b＞0；③≤a≤-，④4≤n＜5中，正确有（　　 ）

A. 1个 B. 2个 C. 3个 D. 4个
12. 如图，以 Rt△ABC的斜边 BC为一边在△ABC的同侧作正方形 BCEF,设正方形的为 O，连接 AO，如果 AB＝4，AO＝6，那么 AC 的长等于（ ）


A. 12 B. 16 C. 4 D. 8
二、填 空 题（每小题4分，共24分）
13. 已知△ABC与△DEF相似且面积比为4：25，则△ABC与△DEF的相似比为_____．
14. 将抛物线y=-x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为 __________________．
15. 如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD，若∠A=25°，则∠C =_______度.

16. 如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为_______．

17. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列三个结论：
①∠BOC=90°+∠A；②设OD＝m，AE＋AF＝n，则S△AEF＝mn；③EF是△ABC的中位线．其中正确的结论是________．

18. 如图，在△ABC中，已知AB=5，BC=8，AC=7，动点P、Q分别在边AB、AC上，使△APQ的外接圆与BC相切，则线段PQ的最小值等于_______________．

三、解 答 题（第19题6分，第20、21题8分，第22～24题各10分，第25题12分，第26题14分，共78分）
19. 计算：；
20. 一个没有透明的袋中装有除颜色外都相同的球，其中红球13个，白球7个、黑球10个．
（1）求从袋中摸一个球是白球的概率；
（2）现从袋中取出若干个红球，放入相同数量的黑球，使从袋中摸出一个球是黑球的概率没有超过40%，问至多取出多少个红球？
21. 如图所示，C城市在A城市正东方向，现计划在A，C两城市间修建一条高速铁路（即线段AC），经测量，森林保护区的P在城市A的北偏东60°方向上，在线段AC上距A城市120km的B处测得P在北偏东30°方向上，已知森林保护区是以点P为圆心，100km为半径的圆形区域，请问计划修建的这条高速铁路是否穿越保护区，为什么．
（参考数据：）

22. 有一批圆心角为90o，半径为3的扇形下脚料，现利用这批材料截取尽可能大的正方形材料，如图有两种截取方法：
方法一：如图1所示，正方形OPQR的顶点P、Q、R均在扇形的边界上；
方法二：如图2所示，正方形顶点C、D、E、F均在扇形边界上．
试分别求这两种截取方法得到的正方形面积，并说明哪种截取方法得到的正方形面积更大．

23. 如图，已知是直径，点在上，是的切线，于点，是延长线上一点，交于点，连接，．

（1）求证：平分；
（2）若，．
①求的度数；
②若的半径为，求线段的长．
24. 如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣x2+x+4A、B两点．

（1）写出点A、点B的坐标；
（2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的面积；
（3）在（2）的条件下，是否存在t，使得△PAM是直角三角形？若存在，请求出点P的坐标；若没有存在，请说明理由．
25. 三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心．按此说法，四边形的四个角平分线交于一点，我们也称为“四边形的内心”．
（1）试举出一个有内心的四边形．
（2）探究：对于任意四边形ABCD，如果有内心，则四边形的边长具备何种条件？为什么？
（3）探究：腰长为的等腰直角三角形ABC，∠C=90°，O是△ABC的内心，若沿图中虚线剪开，O仍然是四边形ABDE的内心，此时裁剪线有多少条？
（4）问题（3）中，O是四边形ABDE内心，且四边形ABDE是等腰梯形，求DE的长？

26. 如图，在平面直角坐标系中，抛物线与轴交于A、B两点（点A在点B的左侧），点B的坐标为（3，0），与轴交于点C（0，-3），顶点为D．
（1）求抛物线的解析式及顶点D的坐标．
（2）联结AC，BC，求∠ACB正切值．
（3）点P是x轴上一点，是否存在点P使得△PBD与△CAB相似，若存在，请求出点P的坐标；若没有存在，请说明理由．
（4）M是抛物线上一点，点N在轴上，是否存在点N，使得以点A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若没有存在，请说明理由．




























2022-2023学年河北省保定市九年级上册数学期末专项突破模拟题（A卷）
一、选一选（每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求）
1. 若，则等于（　　）
A. B. C. D.
【正确答案】B

【详解】由比例的基本性质可知a=，因此=.
故选B.
2. 对于二次函数，下列说法没有正确的是（　　）
A. 有最小值–3 B. 对称轴是直线x = 4
C. 顶点是（4，–3） D. 在对称轴的左侧y随x的增大而增大
【正确答案】D

【详解】根据二次函数的解析式，可知a=2＞0，函数有最小值-3，故A正确；对称轴为x=4，故B正确；顶点为（4，-3），故C正确；在对称轴的左侧y随x增大而减小，故D没有正确.
故选D.
3. 由6个大小相同的正方体搭成的几何体如图所示，则关于它的视图说确的是（　　）

A. 正视图的面积 B. 左视图的面积
C. 俯视图的面积 D. 三个视图的面积一样大
【正确答案】C

【详解】观察图形可知，几何体的正视图由4个正方形组成，俯视图由5个正方形组成，左视图由4个正方形组成，所以俯视图的面积．
故选C．
4. 在Rt△ABC中，∠C=90°，AC=3，AB=5，那么的值是（　　）
A. B. C. D.
【正确答案】B

【详解】根据勾股定理，由∠C=90°，AC=3，AB=5，可求得BC=4，然后根据∠A的正弦等于∠A的对边比斜边，可知sinA=.
故选B.
5. 已知圆锥的母线长为5，底面半径为3，则圆锥的表面积为（　　）
A. 15π B. 24π C. 30π D. 39π
【正确答案】B

【详解】底面半径为3cm，则底面周长=6πcm，圆锥的侧面面积=×6π×5=15πcm2，底面面积=9πcm2，
∴圆锥的表面积=15π+9π=24πcm2．
故选B．
6. 如图所示把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点，把平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的正三角形，那么剪出的正三角形全部展开铺平后得到的平面图形一定是（　　）

A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形
【正确答案】D

【详解】由第二个图形可知：∠AOB被平分成了三个角，每个角为60°，它将成为展开得到图形的角，那么所剪出的平面图形是360°÷60°=6边形．
故选D．
7. 如图，已知梯形中， 点与原点重合，点（4，0）在轴上，则点的坐标是 （　　）

A. （3，2） B. （3，） C. （，2） D. （2，3）
【正确答案】B

【分析】
【详解】解：过点B作BF⊥AD，于点F，过点C作CE⊥AD于点E，

由梯形ABCD中，，点A与原点重合，点D（4，0）在x轴上，



，

AF=1，EF=BC=AB=CD=2，
CE==．
则点C的坐标是：（3，）．
故选：B．
本题主要考查了梯形的性质以及坐标与图形的性质等知识，得出AE的长是解题关键．
8. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，CH┴AF与点H，那么CH的长是（ ）

A. B. C. D.
【正确答案】D

【分析】连接AC、CF，根据正方形性质求出AC、CF，∠ACD=∠GCF=45°，再求出∠ACF=90°，然后利用勾股定理列式求出AF，由直角三角形面积的两种表示法即可求得CH的长.
【详解】如图，连接AC、CF，

∵正方形ABCD和正方形CEFG中，BC=1，CE=3，
∴AC= ，CF=3，
∠ACD=∠GCF=45°，
∴∠ACF=90°，
由勾股定理得，AF=，
∵CH⊥AF，
∴，
即，
∴CH=.
故选D.
本题考查了正方形的性质、勾股定理及直角三角形的面积，熟记各性质并作辅助线构造出直角三角形是解题的关键．
9. 已知点A（a-3b，2-6ab）在抛物线上，则点A关于x轴的对称点坐标为（　　）
A. （6，20） B. （－6，20） C. （6，－20） D. （－6，－20）
【正确答案】D

【详解】根据点在曲线上点的坐标满足方程的关系，把点A坐标（a-3b，2-6ab）代入二次函数解析式y=x2+6x+20，并利用完全平方公式整理为a2+6a+9b2-18b+18=0，即（a+3）2+9（b-1）2=0，然后根据偶次幂的非负数的性质列式求出a=-3、b=1，再求出点A的坐标（-6，20），然后根据对称性求得点A关于x轴的对称点的坐标为（-6，-20）．
故选：D．
点睛：本题考查了二次函数图象上点的坐标特征，关于x轴、y轴对称点的坐标特征，难点在于因式分解整理出两个平方和等于0的形式．
10. 将△ABC绕点B逆时针旋转到△A′BC′使A、B、C′在同一直线上，若∠BCA=90°，∠BAC=30°，AB=4cm，则图中阴影部分面积为（　　）

A 8πcm2 B. cm2 C. cm2 D. 4πcm2
【正确答案】D

【详解】由图可得阴影部分面积为圆心角为120°，两个半径分别为4和2的圆环的面积的差．由∠BCA=90°，∠BAC=30°，AB=4cm，求得BC=2，AC=2，∠A′BA=120°，∠CBC′=120°，所以阴影部分面积=（S△A′BC′+S扇形BAA′）-S扇形BCC′-S△ABC=×（42-22）=4πcm2．
故选D

解题的关键是熟练掌握含30°角的直角三角形的性质：30°角所对的直角边等于斜边的一半.
11. 如图，抛物线y=ax2+bx+c与x轴交于点A（-2，0），顶点坐标为（2，n），与y轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①当x＞6时，y＜0；②5a+b＞0；③≤a≤-，④4≤n＜5中，正确有（　　 ）

A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】B

【详解】根据抛物线的对称性，由点A的坐标（-2，0）和对称轴x=2，得到与x轴的另一个交点为（6，0），然后根据图像可知当x＞6时，y＜0，故①正确；
根据图示知，抛物线开口方向向下，则a＜0．由对称轴x==2，解得b=-4a，所以5a+b=5a-4a=a＜0，即5a+b＜0．故②错误；
根据抛物线与y轴的交点在（0，3），（0，4）之间（包含端点），可得3≤c≤4，令x=-2，则4a-2b+c=0，又由于b=-4a，可得c=-12a，即3≤-12a≤4，解得-≤a≤-，故③正确；
根据抛物线的顶点坐标为，可得n==c-，然后根据b=-4a，3≤c≤4，-≤a≤-，可得n=c-4a，即4≤n≤，故④没有正确.
故选B.
12. 如图，以 Rt△ABC的斜边 BC为一边在△ABC的同侧作正方形 BCEF,设正方形的为 O，连接 AO，如果 AB＝4，AO＝6，那么 AC 的长等于（ ）


A. 12 B. 16 C. 4 D. 8
【正确答案】B

【分析】在上截取，连接，利用可证△ABO≌△GCO，根据全等三角形的性质可以得到：，，则可证△AOG是等腰直角三角形，利用勾股定理求出，从而可得的长度．
【详解】解：如下图所示，
在上截取，连接，
∵四边形是正方形，，
∴，，
∴点、、、四点共圆，
∴，
在△ABO和△GCO中，
，
∴△ABO≌△GCO，
∴，，
∵，
∴，
∴△AOG是等腰直角三角形，
∴，
∴．
故选：B．

本题考查正方形的性质；全等三角形的判定与性质；勾股定理；直角三角形的性质．
二、填 空 题（每小题4分，共24分）
13. 已知△ABC与△DEF相似且面积比为4：25，则△ABC与△DEF的相似比为_____．
【正确答案】2：5．

【详解】相似三角形的性质．
【分析】∵△ABC∽△DEF，∴△ABC与△DEF的面积比等于相似比的平方，
∵，∴△ABC与△DEF的相似比为2：5．
14. 将抛物线y=-x2先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为 __________________．
【正确答案】y=-(x-3) 2 -2 (或y=-x 2 +6x-11)

【详解】解：抛物线先向下平移2个单位，再向右平移3个单位后所得抛物线的解析式为即，
故答案为y=-(x-3) 2 -2 (或y=-x 2 +6x-11)．
本题考查二次函数图象与几何变换．
15. 如图，AB是⊙O的直径，点C在AB的延长线上，CD切⊙O于点D，连接AD，若∠A=25°，则∠C =_______度.

【正确答案】40.

【详解】解：如图，连接OD，
∵∠BOD和∠A是同弧所对的圆心角和圆周角，∠A=25°，
∴∠BOD=2∠A=50°.
∵CD切⊙O于点D，
∴OD⊥CD，即∠ODC=90°.
∴∠C =40°．
故40．

考点：1. 圆周角定理；2.切线的性质；3.直角三角形两锐角的关系.

16. 如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为_______．

【正确答案】

【分析】根据AAS可以证明△ABE≌△ECF，得AB=CE，BE=CF；根据两角对应相等，可以证明△ECF∽△FDG，则DF：CE=FG：EF=1：2．设BE=x，则AB=2x，根据勾股定理求得x的值，进而求得矩形的周长．
【详解】解：根据等角的余角相等，得
∠BAE=∠CEF=∠DFG．
又∠B=∠C=∠D=90°，AE=EF=4，FG=2，
∴△ABE≌△ECF，△ECF∽△FDG．
∴AB=CE，BE=CF，DF：CE=FG：EF=1：2．

设BE=x，则AB=2x，根据勾股定理，得
x2+4x2=16，
x=．
则矩形ABCD的周长为：
故
17. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列三个结论：
①∠BOC=90°+∠A；②设OD＝m，AE＋AF＝n，则S△AEF＝mn；③EF是△ABC的中位线．其中正确的结论是________．

【正确答案】①

【详解】∵在△ABC中，∠ABC和∠ACB的平分线相交于点O，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∵∠ABC+∠ACB=180°-∠A，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（∠ABC+∠ACB）=90°+∠A；故①正确；

连接AO，过点O作OH⊥AB于H，
∴AO是△ABC的角平分线，
∵OD⊥AC，
∴OH=OD=m，
∴S△AEF=S△AOE+S△AOF=AE•OH+AF•OD=OD•（AE+AF）=mn；故②错误；
若△ABC是等边三角形，则三线合一，此时EF是△ABC的中位线；故③错误.
故答案为①.
点睛：此题考查了角平分线的性质，等腰三角形的判定与性质，以及圆与圆的位置关系等知识．此题综合性较强，难度较大，解题的关键是注意数形思想的应用，注意辅助线的作法．
18. 如图，在△ABC中，已知AB=5，BC=8，AC=7，动点P、Q分别在边AB、AC上，使△APQ的外接圆与BC相切，则线段PQ的最小值等于_______________．

【正确答案】

【详解】如图，设点O是△APQ的外接圆的圆心，连接OP，OQ，作OH⊥PQ于点H，过点A作AD⊥BC于点D，

∴PH=QH=PQ，
∵OP=OQ，
∴∠POH=∠POQ，
∵∠POQ=2∠BAC，
∴∠POH=∠BAC，
在Rt△POH中，PH=OP•sin∠POH=OA•sin∠BAC，
∴PQ=2OA•sin∠BAC，
即当OA最小时，PQ最小，
∵当AD是直径时，即OA=AD时，PQ最小，
设BD=x，则CD=8-x，
∵在Rt△ABD中，AD2=AB2-AD2，
在Rt△ACD中，AD2=AC2-CD2，
∴25-x2=49-（8-x）2，
解得：x= ，
∴AD== ，
∴OA=，
设AC边上的高为h，
则AC•h=BC•AD，
∴h= ，
∴sin∠BAC==，
∴PQ=2OA•sin∠BAC=2××= ．
故答案为．
点睛：此题考查了切线的性质、三角形外接圆的性质、勾股定理以及三角函数等知识．此题难度较大，注意掌握辅助线的作法，注意数形思想与方程思想的应用．
三、解 答 题（第19题6分，第20、21题8分，第22～24题各10分，第25题12分，第26题14分，共78分）
19. 计算：；
【正确答案】解：原式＝2＋1＋1－2＝2

【详解】根据值、幂的性质及角的锐角三角函数值计算．
20. 一个没有透明的袋中装有除颜色外都相同的球，其中红球13个，白球7个、黑球10个．
（1）求从袋中摸一个球是白球的概率；
（2）现从袋中取出若干个红球，放入相同数量的黑球，使从袋中摸出一个球是黑球的概率没有超过40%，问至多取出多少个红球？
【正确答案】（1）；（2）2．

【详解】试题分析：（1）因为袋中共有30个球，其中白球7个，所以从袋中摸一个球是白球的概率；（2）设取出x个红球，然后根据：从袋中摸出一个球是黑球的概率没有超过40%,列没有等式可解决问题．
试题解析：(1）P(白）=
(2）设取出x个红球
由题意得≤40%
解得x≤2
答：至多取出2个红球．
考点：1．简单的概率；2．没有等式的应用．
21. 如图所示，C城市在A城市正东方向，现计划在A，C两城市间修建一条高速铁路（即线段AC），经测量，森林保护区的P在城市A的北偏东60°方向上，在线段AC上距A城市120km的B处测得P在北偏东30°方向上，已知森林保护区是以点P为圆心，100km为半径的圆形区域，请问计划修建的这条高速铁路是否穿越保护区，为什么．
（参考数据：）

【正确答案】这条高速公路没有会穿越保护区，理由见解析．

【分析】作PH⊥AC于H．求出PH与100比较即可解决问题．
【详解】解：结论；没有会．理由如下：
作PH⊥AC于H．

由题意可知：∠EAP=60°，∠FBP=30°，
∴∠PAB=30°，∠PBH=60°，
∵∠PBH=∠PAB+∠APB，
∴∠BAP=∠BPA=30°，
∴BA=BP=120，
Rt△PBH中，sin∠PBH=，
∴PH=PBsin60°=120×≈103.92，
∵103.80＞100，
∴这条高速公路没有会穿越保护区．
本题考查解直角三角形的应用．
22. 有一批圆心角为90o，半径为3的扇形下脚料，现利用这批材料截取尽可能大的正方形材料，如图有两种截取方法：
方法一：如图1所示，正方形OPQR的顶点P、Q、R均在扇形的边界上；
方法二：如图2所示，正方形顶点C、D、E、F均在扇形边界上．
试分别求这两种截取方法得到的正方形面积，并说明哪种截取方法得到的正方形面积更大．

【正确答案】方法一：S1=；方法二：S2=．方法一的面积更大．

【详解】试题分析：根据题意画出图形，分别连接PQ和过O作OG⊥DE，交CF于点H，连接OF，构造直角三角形求得正方形的边长，求得正方形的面积后比较即可．由于正方形内接于扇形，故应分两种情况进行讨论．
试题解析：解：方法一：如图1

连结OQ
∵OQ=3，四边形OPQR为正方形
∴S1=3×3÷2=
方法二：如图2
过O作OH⊥EF
设FH=a 则OH=3a
在Rt△OHF中
∴

解得：
∴EF=
∴S2==
∵S1＞S2 ∴方法一面积更大
点睛：本题考查的是垂径定理及勾股定理，解答此题的关键是根据题意画出图形，作出辅助线，构造出直角三角形，再进行解答．
23. 如图，已知是的直径，点在上，是的切线，于点，是延长线上一点，交于点，连接，．

（1）求证：平分；
（2）若，．
①求的度数；
②若的半径为，求线段的长．
【正确答案】（1）见解析；（2）①；②

【分析】（1）由切线性质知OC⊥CD，AD⊥CD得AD∥OC，即可知∠DAC＝∠OCA＝∠OAC，从而得证；
（2）①由AD∥OC知∠EOC＝∠DAO＝105°，∠E＝30°可得答案；
②作OG⊥CE，根据垂径定理及等腰直角三角形性质知CG＝FG＝OG，由得出CG＝FG＝OG＝2，在Rt△OGE中，由∠E＝30°可得答案．
【详解】（1）证明：∵直线与相切
∴．
又∵，
∴．
∴
又∵，
∴．
∴．
∴平分．
（2）①∵，，
∴
∵，
∴．
②作于点，可得
∵，
∴
∴
∵在中，，
∴
∴
本题主要考查圆的切线的性质、平行线的判定与性质、垂径定理及等腰直角三角形性质，熟练掌握切线的性质、平行线的判定与性质、垂径定理及等腰直角三角形性质是解题的关键．
24. 如图，在等腰三角形ABC中，AB=AC，以底边BC的垂直平分线和BC所在的直线建立平面直角坐标系，抛物线y=﹣x2+x+4A、B两点．

（1）写出点A、点B的坐标；
（2）若一条与y轴重合的直线l以每秒2个单位长度的速度向右平移，分别交线段OA、CA和抛物线于点E、M和点P，连接PA、PB．设直线l移动的时间为t（0＜t＜4）秒，求四边形PBCA的面积S（面积单位）与t（秒）的函数关系式，并求出四边形PBCA的面积；
（3）在（2）的条件下，是否存在t，使得△PAM是直角三角形？若存在，请求出点P的坐标；若没有存在，请说明理由．
【正确答案】（1）A（8，0）、B（0，4）;（2）S=﹣8t2+32t+32,S值为64．（3）存在符合条件的点P，坐标为（3，10）．

【详解】试题分析：（1）抛物线的解析式中，令x=0，能确定点B的坐标；令y=0，能确定点A的坐标．（2）四边形PBCA可看作△ABC、△PBA两部分；△ABC的面积是定值，关键是求出△PBA的面积表达式；若设直线l与直线AB的交点为Q，先用t表示出线段PQ的长，而△PAB的面积可由（PQ•OA）求得，在求出S、t的函数关系式后，由函数的性质可求得S的值．（3）△PAM中，∠APM是锐角，而PM∥y轴，∠AMP=∠ACO也没有可能是直角，所以只有∠PAC是直角一种可能，即 直线AP、直线AC垂直，此时两直线的斜率乘积为-1，先求出直线AC的解析式，联立抛物线的解析式后可求得点P的坐标．
试题解析：
（1）抛物线y=﹣0.5x2+3.5x+4中：令x=0，y=4，则 B（0，4）；
令y=0，0=﹣0.5x2+3.5x+4，解得 x1=﹣1、x2=8，则 A（8，0）；∴A（8，0）、B（0，4）．
（2）△ABC中，AB=AC，AO⊥BC，则OB=OC=4，∴C（0，﹣4）．
由A（8，0）、B（0，4），得：直线AB：y=﹣0.5x+4；
依题意，知：OE=2t，即 E（2t，0）；
∴P（2t，﹣2t2+7t+4）、Q（2t，﹣t+4），PQ=（﹣2t2+7t+4）﹣（﹣t+4）=﹣2t2+8t；
S=S△ABC+S△PAB=0.5×8×8+0.5×（﹣2t2+8t）×8=﹣8t2+32t+32=﹣8（t﹣2）2+64；
∴当t=2时，S有值，且值64．
（3）∵PM∥y轴，∴∠AMP=∠ACO＜90°；
而∠APM是锐角，所以△PAM若是直角三角形，只能是∠PAM=90°；
由A（8，0）、C（0，﹣4），得：直线AC：y=0.5x﹣4；
所以，直线AP可设为：y=﹣2x+h，代入A（8，0），得：﹣16+h=0，h=16
∴直线AP：y=﹣2x+16，联立抛物线的解析式，∴存在符合条件的点P，且坐标为（3，10）．

点睛：此题主要考查的是函数图象与坐标轴的交点坐标的求法、图形面积的解法以及直角三角形的判定；一题中，先将没有可能的情况排除掉，可的简化解答过程．
25. 三角形角平分线交点或三角形内切圆的圆心都称为三角形的内心．按此说法，四边形的四个角平分线交于一点，我们也称为“四边形的内心”．
（1）试举出一个有内心的四边形．
（2）探究：对于任意四边形ABCD，如果有内心，则四边形的边长具备何种条件？为什么？
（3）探究：腰长为的等腰直角三角形ABC，∠C=90°，O是△ABC的内心，若沿图中虚线剪开，O仍然是四边形ABDE的内心，此时裁剪线有多少条？
（4）问题（3）中，O是四边形ABDE内心，且四边形ABDE是等腰梯形，求DE的长？

【正确答案】（1）正方形，菱形（写出一个即可） ；（2）对边之和相等；（3）有无数条 ；（4）．

【详解】试题分析：（1）对角线平分每一对角的四边形都可以，如菱形、正方形；
（2）对于任意四边形ABCD，如果有内心，则四边形的边长具备条件是对边和相等；
（3）根据O到AB的距离等于O到DE的距离，即可得到答案；
（4）由勾股定理求出AB=2，过D作DF⊥AB于F，过E作EQ⊥AB于Q，得到平行四边形DEQF，推出DE=FQ，DF=EQ，根据等腰直角三角形得出AF=DF=BQ=QE，设DC=x，由勾股定理求出DE、AF、BQ的长，即AF+FQ+BQ=2，代入即可求出答案．
试题解析：（1）答：一个有内心的四边形是菱形．
（2）答：对于任意四边形ABCD，如果有内心，则四边形的边长具备条件是对边和相等．
（3）解：有无数条，
理由是根据角平分线的性质得到：O到AB的距离等于O到DE的距离，在△ABC内有无数条，如图：具备DE∥AB即可．

（4）解：等腰直角三角形ACB，AC=BC=2，由勾股定理得：AB=2，
过D作DF⊥AB于F，过E作EQ⊥AB于Q，

∴DF∥EQ，
∵DE∥AB，
∴四边形DEQF是平行四边形，
∴DE=FQ，DF=EQ，
∵∠A=∠B=45°，
∴AF=DF，
同理BQ=QE，
设DE=x，AB=2，过C作CM⊥BC，交DE与N点，
由AB=AC，根据三线合一可得CM=，
由三角形的面积有两种求法，S=AC•BC=（AC+BC+AB）•OM，
即4=（2+2+2）×OM，解得：OM=2-，
∴NM=2OM=4-2，CN=-（4-2）=3-4，
又△CDE∽△CAB，
∴=，即=，
解得：x=6-8，
则DE=6-8．
点睛：本题主要考查对平行四边形的性质和判定，勾股定理，角平分线的性质，三角形的内切圆与内心，等腰题型的性质等知识点的理解和掌握，此题是一个拔高的题目，有一定难度．
26. 如图，在平面直角坐标系中，抛物线与轴交于A、B两点（点A在点B的左侧），点B的坐标为（3，0），与轴交于点C（0，-3），顶点为D．
（1）求抛物线的解析式及顶点D的坐标．
（2）联结AC，BC，求∠ACB的正切值．
（3）点P是x轴上一点，是否存在点P使得△PBD与△CAB相似，若存在，请求出点P的坐标；若没有存在，请说明理由．
（4）M是抛物线上一点，点N在轴上，是否存在点N，使得以点A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若没有存在，请说明理由．

【正确答案】（1），D（1，-4）；（2）2；（3）P（，0）或P（－3，0）；（4）N（1，0）或（，0）或（－3，0）．

【分析】（1）利用待定系数法，把B、C点的坐标代入解析式即可求解，进一步即可求出点D的坐标；
（2）作AH⊥BC于点H，通过与x轴的交点y=0构成方程，解方程可得A点的坐标，然后解直角三角形可求解；
（3）作DG⊥OB于点G ，tan∠DBG=tan∠ACB，可得∠DBG=∠ACB，然后利用相似三角形的性质和判定讨论得到P点在点B的左侧，再根据相似三角形的对应边成比例求解即可；
（4）设N点的坐标为（x，0），然后根据A、C点和MZ在抛物线上，平行四边形的性质与判定求出N点的坐标即可．
【详解】解：（1）把 点B、C的坐标代入，得，
解得：b=-2，c=-3，
∴抛物线的解析式是y=x2-2x-3；
∵y=x2-2x-3=（x-1）2-4，
∴顶点D（1，-4）
（2）作AH⊥BC于点H，

由x2-2x-3=0，解得x=-1或x=3，
所以A点为（-1，0）
∵ OB=OC=3，∠BOC=90°，
∴∠OBC=45°，
∵AB=4，
∴AH=BH=2，
∵BC=3，
∴CH=，
∴tan∠ACB=CH：AH=2；
（3）作DG⊥OB于点G，
∵BG=2，DG=4，
∴tan∠DBG=2，
∵tan∠ACB=2，
∴∠DBG=∠ACB，
当点P在点B右侧时，∠PBD＞90°，△PBD是钝角三角形与△CAB没有相似，
所以点P在点B的左侧；
∵△PBD与△CAB相似，且∠DBG=∠ACB，
∴或
∵BD=2，
∴BP=或BP=6，
∴P（-，0）或P（-3，0）；

（4）设N点的坐标为（x，0），
若AC为边，则由平移的性质可得M的坐标可表示为（x+1，-3）或（x-1，3），
代入抛物线的解析式可得：（x+1）2-2（x+1）-3=-3，或（x-1）2-2（x-1）-3=3，
解得x=1，或x=，
若AC为对角线，则由AN∥CM可得点N的坐标为（-3，0）
∴点N存在，且N（1，0）或（，0）或（－3，0）．
本题是二次函数的综合题，主要考查了待定系数法求二次函数的解析式、解直角三角形、平行四边形的性质等知识，属于中考压轴题，熟练掌握相关知识、灵活应用数形的思想是解题的关键．







2022-2023学年河北省保定市九年级上册数学期末专项突破模拟题（B卷）
一、精心选一选，慧眼识金！（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中只需一项是正确的）
1. 若代数式有意义，则x取值范围是（ ）
A. B. ≥ C. ≤ D. ≠-
2. 下列一元二次方程中，有两个相等的实数根的是（ ）
A. B.
C. D.
3. 下列计算正确的是（　　）
A. B. C. D.
4. 如图，⊙O是△ABC的外接圆，∠A =40°，则∠OCB等于（ ）

A 60° B. 50° C. 40° D. 30°
5. 将抛物线y=x2平移得到抛物线y=x2+5，下列叙说正确的是（ ）
A. 向上平移5个单位 B. 向下平移5个单位
C. 向左平移5个单位 D. 向右平移5个单位
6. 如图，平面直角坐标系中的二次函数图象所对应的函数解析式可能为（ ）

A. B.
C. D.
7. 一件商品的原价是100元，两次降价后的价格为121元，如果每次降价的百分率都是x，根据题意，上面列出的方程正确的是（ ）
A. 100(1+x)=121 B. 100(1-x)=121 C. 100(1+x)2=121 D. 100(1-x)2=121
8. 某学校组织艺术摄影展，上交的作品要求如下：七寸照片（长7英寸，宽5英寸）；将照片贴在一张矩形衬纸的正，照片周围外露衬纸的宽度相反；矩形衬纸的面积为照片面积的3倍．设照片周围外露衬纸的宽度为x英寸（如图），上面所列方程正确的是（　　）

A. （7+x）（5+x）×3=7×5 B. （7+x）（5+x）=3×7×5
C. （7+2x）（5+2x）×3=7×5 D. （7+2x）（5+2x）=3×7×5

9. 如图，直线与轴、轴分别交于、两点，△绕点顺时针旋转90°后得到△，则点对应点坐标为（ ）

A. （3，4） B. （7，4）
C. （7，3） D. （3，7）
10. 在同一坐标系中，函数y=ax+1与二次函数y=x2+a的图象可能是（ ）
A. B. C. D.
二、填 空 题（简约的结果，表达的是你敏锐的思想，需求的是细心！每小题3分，共30分）
11. 一个图形无论平移还是旋转，以下说法：①对应线段平行；②对应线段相等；③对应角相等；④图形的外形和大小都没有发生变化．其中说确的是________．
12. 如图，⊙O的弦AB＝8，OD⊥AB于点D，OD＝3，则⊙O的半径等于_____．

13. 如图是二次函数y＝ax2＋bx＋c的部分图象，由图象可知方程ax2＋bx＋c＝0的解是_____，_____．

14. 如图，点B，A，C，D在⊙O上，OA⊥BC，∠AOB=50°，则∠ADC=__．

15. 若两圆的半径分别是2和3，圆心距是5，则这两圆的地位关系是_____．
16. 在一个不透明袋中装有五个除数字外其它完全相反的小球，球面上分别写有0，1，2，3，4这5个数字，玲玲从袋中任意摸出一个小球，球面数字的平方根是有理数的概率是_____．
17. 如图，AB是⊙O的直径，点C在⊙O上，∠BAC=43o，点P在线段OB上运动，设∠ACP=x，则x的取值范围是__________________．

18. 一个扇形的圆心角为120°，半径为3cm，则这个扇形的面积为_______cm2
19. 小红要过生日了，为了筹备生日聚会，预备本人动手用纸板制造一个底面半径为9cm，母线长为30cm的圆锥形生日礼帽，则这个圆锥形礼帽的侧面积为_____cm2 ．（结果保留）
20. 已知二次函数的图像如图所示，下列4个结论：①；②；③；④．其中正确的结论有__________．

三、解 答 题（耐心计算，认真推理，表露你萌动的智慧！共60分）
21. 计算：
22. 用配方法解方程：
23. 如图，点A、B、C分别是⊙O上的点，∠B=60°，CD是⊙O的直径，P是CD延伸线上的一点，且AP=AC.
求证：AP是⊙O切线.

24. 如图，AB是⊙O的直径，CD是⊙O的一条弦，且CO⊥AB于点E．
（1）求证：∠BCO＝∠D．
（2）若CD＝4，AE＝2，求⊙O的半径．

25. 某校举行以“助桀为虐，乐在其中”为主题的演讲比赛，比赛设一个名，一个第二名，两个并列第三名．前四名中七、八年级各有一名同窗，初三有两名同窗，小蒙同窗认为前两名是初三同窗的概率是，你赞成他的观点吗？请用列表法或画树形图法分析阐明．
26. 如图，矩形ABCD中，AB=16cm，AD=4cm，点P、Q分别从A、B同时出发，点P在边AB上沿AB方向以2cm/s的速度匀速运动，点Q在边BC上沿BC方向以1cm/s的速度匀速运动，当其中一点到达起点时，另一点也随之中止运动.设运动工夫为x秒，△PBQ的面积为y（cm2）.
（1）求y关于x函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的值.，并指出此时x的值.
















2022-2023学年河北省保定市九年级上册数学期末专项突破模拟题（B卷）
一、精心选一选，慧眼识金！（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中只需一项是正确的）
1. 若代数式有意义，则x的取值范围是（ ）
A. B. ≥ C. ≤ D. ≠-
【正确答案】B

【详解】试题分析：若代数式有意义，则二次根式上面的数为非负数，即
考点：代数式有意义
点评：本题考查代数式有有意义，考生要熟习代数式有意义的几种情况
2. 下列一元二次方程中，有两个相等的实数根的是（ ）
A. B.
C. D.
【正确答案】A

【详解】A.△=(−2)2−4×1×1=0，有两个相等的实数根，故本选项正确；
B.△=22−4×1×(−4)>0，有两个不相等实数根，故本选项错误；
C.△=(−2)2−4×1×(−5)>0，有两个不相等实数根，故本选项错误；
D.△=22−4×1×4<0，无实数根，故本选项错误.
故选A.
3. 下列计算正确的是（　　）
A. B. C. D.
【正确答案】C

【分析】根据合并二次根式的法则、二次根式的性质、二次根式的除法法则即可判定．
【详解】A、不能合并，故选项A错误；
B、，故选项B错误；
C、，故选项C正确；
D、，故选项D错误；
故选：C．
本题考查了二次根式的混合运算，纯熟掌握二次根式的运算法则是解题的关键．
4. 如图，⊙O是△ABC的外接圆，∠A =40°，则∠OCB等于（ ）

A. 60° B. 50° C. 40° D. 30°
【正确答案】B

【详解】∵∠A=40°，
∴∠BOC=80°，
∵BO=CO，
∴∠OCB=(180°−80°)÷2=50°，
故选B.
5. 将抛物线y=x2平移得到抛物线y=x2+5，下列叙说正确的是（ ）
A. 向上平移5个单位 B. 向下平移5个单位
C. 向左平移5个单位 D. 向右平移5个单位
【正确答案】A

【详解】试题分析：按照“左加右减，上加下减”．将抛物线y=x2向上平移5个单位得到抛物线y=x2+5，故选A．
【考点】二次函数图象与几何变换．
6. 如图，平面直角坐标系中的二次函数图象所对应的函数解析式可能为（ ）

A. B.
C. D.
【正确答案】D

【详解】由图象可得二次函数顶点坐标位于第三象限，所以
A.的顶点为（0，0），故错误；
B.的顶点为（-1，0），故错误；
C.的顶点为（1，-1），故错误；
D. 的顶点为（-1，-1），故正确.
故选D.
7. 一件商品原价是100元，两次降价后的价格为121元，如果每次降价的百分率都是x，根据题意，上面列出的方程正确的是（ ）
A. 100(1+x)=121 B. 100(1-x)=121 C. 100(1+x)2=121 D. 100(1-x)2=121
【正确答案】C

【详解】对于增长率的成绩的基本公式为：增长前的数量×=增长后的数量，
由题意，可列方程为：100(1+x)2=121，
故C
8. 某学校组织艺术摄影展，上交的作品要求如下：七寸照片（长7英寸，宽5英寸）；将照片贴在一张矩形衬纸的正，照片周围外露衬纸的宽度相反；矩形衬纸的面积为照片面积的3倍．设照片周围外露衬纸的宽度为x英寸（如图），上面所列方程正确的是（　　）

A. （7+x）（5+x）×3=7×5 B. （7+x）（5+x）=3×7×5
C. （7+2x）（5+2x）×3=7×5 D. （7+2x）（5+2x）=3×7×5
【正确答案】D

【分析】根据关键语句“矩形衬纸的面积为照片面积的3倍”列出方程求解即可．
【详解】解：设照片周围外露衬纸的宽度为x英寸，根据题意得：（7+2x）（5+2x）=3×7×5，
故选：D
找到题中的等量关系，根据两个矩形的面积3倍的关系得到方程，留意的是矩形的间距都为等量的，从而得到大矩形的长于宽，用未知数x的代数式表示，而列出方程，属于基础题．

9. 如图，直线与轴、轴分别交于、两点，△绕点顺时针旋转90°后得到△，则点的对应点坐标为（ ）

A. （3，4） B. （7，4）
C. （7，3） D. （3，7）
【正确答案】C

【详解】当x=0时，y=−x+4=4，则B点坐标(0，4)；
当y=0时，−x+4=0，解得x=3，则A点坐标为(3，0)，
则OA=3，OB=4，
∵△AOB绕点A顺时针旋转90°后得到△AO′B′，
∴∠OAO′=90°，∠AO′B′=∠AOB=90°，AO′=AO=3，O′B′=OB=4，
即AO′⊥x轴，O′B′∥x轴，
∴点B′坐标为(7，3).
故选C.
10. 在同一坐标系中，函数y=ax+1与二次函数y=x2+a的图象可能是（ ）
A. B. C. D.
【正确答案】C

【分析】本题可先由函数y=ax+1图象得到字母系数的正负，再与二次函数y=x2+a的图象相比较，看能否分歧．
【详解】A．由抛物线y轴的交点在y轴的负半轴上可知，a＜0，由直线可知，a＜0，错误；
B．由抛物线与y轴的交点在y轴的正半轴上可知，a＞0，二次项系数为负数，与二次函数y=x2+a矛盾，错误；
C．由抛物线与y轴的交点在y轴的负半轴上可知，a＜0，由直线可知，a＜0，正确；
D．由直线可知，直线（0，1），错误．
故选：C．
正确理解函数和二次函数的性质是解答本题的关键.
二、填 空 题（简约的结果，表达的是你敏锐的思想，需求的是细心！每小题3分，共30分）
11. 一个图形无论平移还是旋转，以下说法：①对应线段平行；②对应线段相等；③对应角相等；④图形的外形和大小都没有发生变化．其中说确的是________．
【正确答案】②③④

【分析】根据平移和旋转的性质解答即可．
【详解】解：根据平移的性质可知：平移变换对应线段平行或共线；对应线段相等；对应角相等；图形的外形和大小没有发生变化；
根据旋转的性质可知：旋转后对应线段不平行；对应线段相等；对应角相等；图形的外形和大小没有发生变化，
所以②③④正确．
本题次要考查了图形平移的性质和图形旋转的性质，熟记平移和旋转的性质是解题的关键．
12. 如图，⊙O的弦AB＝8，OD⊥AB于点D，OD＝3，则⊙O的半径等于_____．

【正确答案】5

【详解】试题分析：解：连接OA,由于弦与半径垂直，构建直角三角形，由勾股定理求得，∵OD⊥AB，OD= 3, AB=8∴AD=4.AO2=AD2+OD2，即AO2=42+32∴AO=5
考点：垂径定理，勾股定理．
点评：熟知以上两定理，由已知易得，本题属于基础题，难度小，易做得．
13. 如图是二次函数y＝ax2＋bx＋c的部分图象，由图象可知方程ax2＋bx＋c＝0的解是_____，_____．

【正确答案】 ①. -1 ②. 5

【分析】根据抛物线的对称轴的定义、抛物线的图象来求该抛物线与x轴的两交点的横坐标．
【详解】解：由图象可知对称轴x=2，与x轴的一个交点横坐标是5，它到直线x=2的距离是3个单位长度，所以另外一个交点横坐标是-1．
所以x1=-1，x2=5．
故答案是：x1=-1，x2=5．
本题考查了抛物线与x轴的交点，抛物线与x轴两个交点的横坐标的和除以2后等于对称轴．
14. 如图，点B，A，C，D在⊙O上，OA⊥BC，∠AOB=50°，则∠ADC=__．

【正确答案】25°

【详解】解：∵OA⊥BC，
∴，
∴∠ADC=∠AOB= ×50°=25°
15. 若两圆的半径分别是2和3，圆心距是5，则这两圆的地位关系是_____．
【正确答案】外切.

【详解】试题分析：根据两圆的地位关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），外离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）．因此，
∵两圆的半径分别是2和3，圆心距是5，
∴2+3=5，即两圆圆心距离等于两圆半径之和.
∴这两圆的地位关系是外切.
考点：两圆的地位关系.
16. 在一个不透明袋中装有五个除数字外其它完全相反的小球，球面上分别写有0，1，2，3，4这5个数字，玲玲从袋中任意摸出一个小球，球面数字的平方根是有理数的概率是_____．
【正确答案】

【详解】球面上的数字1，2，3，4，5的平方根分别为：0，±1，±，±，±2，.
其中0、±1、±2是有理数，即0、1、4这3个数的平方根是有理数，
则概率公式，可得任意摸出1个小球，球面数字的平方根是有理数的概率是.
17. 如图，AB是⊙O的直径，点C在⊙O上，∠BAC=43o，点P在线段OB上运动，设∠ACP=x，则x的取值范围是__________________．

【正确答案】43°≤x≤90°

【详解】试题分析：分别从若点P与点O重合与若点P与点B重合去分析求解即可求得答案
解：若点P与点O重合，
∵OA=OC，
∴x=∠ACP=∠BAC=43°；
若点P与点B重合，
∵AB是直径，
∴x=∠ACB=90°，
∴x的取值范围是：43°≤x≤90°
考点：圆周角定理
点评：此题考查了圆周角定理与等腰三角形的性质．此题难度适中，留意掌握数形思想与分类讨论思想的运用
18. 一个扇形的圆心角为120°，半径为3cm，则这个扇形的面积为_______cm2
【正确答案】3π

【详解】试题分析：此题考查扇形面积计算，熟记扇形面积公式，即可求解.
根据扇形面积公式，计算这个扇形的面积为.
考点：扇形面积的计算

19. 小红要过生日了，为了筹备生日聚会，预备本人动手用纸板制造一个底面半径为9cm，母线长为30cm的圆锥形生日礼帽，则这个圆锥形礼帽的侧面积为_____cm2 ．（结果保留）
【正确答案】270π．

【详解】试题分析：求圆锥侧面积需求知道圆的半径，母线长，∵半径=9cm，母线=30cm，∴侧面积=9×30．
考点：圆锥侧面积公式．
点评：熟知圆锥侧面积公式，由已知易求，本题属于基础题．
20. 已知二次函数图像如图所示，下列4个结论：①；②；③；④．其中正确的结论有__________．

【正确答案】①②④

【分析】根据抛物线的开口方向可判断a的符号，根据图象与y轴的交点可判断c的符号，根据a的符号及对称轴的地位可判断b的符号，即可对①进行判断；根据x=-1和x=2时y值的大小可对②③进行判断；根据图象与x轴的交点个数可对④进行判断；综上即可得答案．
【详解】∵抛物线的开口向上，
∴a＞0，
∵图象与y轴交于y轴正半轴，
∴c＞0，
∵对称轴在y轴右侧，
∴a、b异号，
∴b＜0，
∴abc＜0，故①正确，
由图象可知，当x=-1时，a-b+c＞0，
∴b＜a+c，故②正确，
当x=2时，4a+2b+c＜0，故③错误，
∵抛物线与x轴有2故交点，
∴b2-4ac＞0，故④正确，
综上所述：正确的结论有①②④．
故①②④
本题考查二次函数y=ax2+bx+c（a≠0）的图象与系数的关系，①二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|还可以决定开口大小，|a|越大开口就越小；②项系数b和二次项系数a共同决定对称轴的地位：当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右，（简称：左同右异）；③常数项c决定抛物线与y轴交点，抛物线与y轴交于（0，c）；④抛物线与x轴交点个数：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．纯熟掌握相关知识是解题关键．
三、解 答 题（耐心计算，认真推理，表露你萌动的智慧！共60分）
21. 计算：
【正确答案】

【分析】先把各二次根式化为最简二次根式，再利用多项式除以单项式的法则进行计算.
【详解】解：原式=


22. 用配方法解方程：
【正确答案】

【详解】试题分析：直接利用配方法解方程得出答案．
试题解析：x2+4x=−2，
x2+4x+4=2，
(x+2)2=2，
x+2=±，
解得：
23. 如图，点A、B、C分别是⊙O上的点，∠B=60°，CD是⊙O的直径，P是CD延伸线上的一点，且AP=AC.
求证：AP是⊙O的切线.

【正确答案】详见解析.

【详解】试题分析：首先连接OA，由∠B=60°，利用圆周角定理，即可求得∠AOC的度数，又由OA=OC，即可求得∠OAC与∠OCA的度数，利用三角形外角的性质，求得∠AOP的度数，又由AP=AC，利用等边对等角，求得∠P，则可求得∠PAO=90°，则可证得AP是 O的切线.
试题解析：连接OA，
∵∠B=60°，
∴∠AOC=2∠B=120°，
∵OA=OC，
∴∠ACP==30°，
又∵AP=AC.
∴∠P=∠ACP=30°，
∴∠PAC =120°，
∴∠OAP=90°，
即OA⊥AP，
∴AP是⊙O的切线.
24. 如图，AB是⊙O的直径，CD是⊙O的一条弦，且CO⊥AB于点E．
（1）求证：∠BCO＝∠D．
（2）若CD＝4，AE＝2，求⊙O的半径．

【正确答案】（1）证明见解析；（2）3

【分析】（1）由，利用等边对等角得到，再由同弧所对的圆周角相等得到，等量代换即可得证；
（2）由弦与直径垂直，利用垂径定理得到为的中点，求出的长，在直角三角形中，设圆的半径，，表示出，利用勾股定理列出关于的方程，求出方程的解即可得到圆的半径的值．
【详解】解：（1），
．
，
；
（2）是的直径，且于点，
，
在中，，
设的半径为，则，，
，
解得：，
的半径为3．
此题考查了垂径定理，勾股定理，以及同弧所对的圆周角相等，纯熟掌握定理是解本题的关键．
25. 某校举行以“助桀为虐，乐在其中”为主题的演讲比赛，比赛设一个名，一个第二名，两个并列第三名．前四名中七、八年级各有一名同窗，初三有两名同窗，小蒙同窗认为前两名是初三同窗的概率是，你赞成他的观点吗？请用列表法或画树形图法分析阐明．
【正确答案】不赞同，.

【分析】首先记七、八年级两名同窗为A，B，初三两名同窗为C，D，然后根据题意画出树状图，由树状图求得一切等可能的结果与前两名是初三同窗的情况，再利用概率公式即可求得答案．
【详解】解：不赞成小蒙同窗的观点．
记七、八年级两名同窗为A，B，初三两名同窗为C，D．
画树形图分析如下：

由上图可知一切的结果有12种，它们出现的可能性相等，满足前两名是初三同窗的结果有2种，所以前两名是初三同窗的概率为．
26. 如图，矩形ABCD中，AB=16cm，AD=4cm，点P、Q分别从A、B同时出发，点P在边AB上沿AB方向以2cm/s的速度匀速运动，点Q在边BC上沿BC方向以1cm/s的速度匀速运动，当其中一点到达起点时，另一点也随之中止运动.设运动工夫为x秒，△PBQ的面积为y（cm2）.
（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的值.，并指出此时x的值.

【正确答案】（1）y=-x2+8x，自变量取值范围0
【详解】试题分析：（1）根据矩形的对边相等表示出BC，然后表示出PB、QB，再根据三角形的面积列式整理即可得解，根据点Q先到达起点确定出x的取值范围即可；
（2）利用二次函数的最值成绩解答．
试题解析：（1）∵四边形ABCD是矩形，
∴BC=AD=4，
根据题意，AP=2x，BQ=x，
∴PB=16−2x，
∵S△PBQ=PB⋅QB，
∴y=−x2+8x，
∵点P的速度是2cm/s，点Q的速度是1cm/s，
∴点P到达起点的工夫是16÷2=8秒，
点Q到达起点的工夫是4÷1=4秒，
∵一点到达起点时，另一点也随之中止运动，
∴自变量取值范围：0 （2）∵y=−x2+8x=−(x−4)2+16，
∴当x=4时，y有值，值为16，
∴△PBQ的面积的值为16cm2.
点睛：本题考查了矩形的性质，二次函数的最值成绩，次要利用了矩形的对边相等的性质，三角形的面积，用x表示出PB、QB是解题的关键.