2022-2023学年贵州省遵义市九年级上册数学期末专项突破模拟题（AB卷）含解析

这是一份2022-2023学年贵州省遵义市九年级上册数学期末专项突破模拟题（AB卷）含解析，共45页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年贵州省遵义市九年级上册数学期末专项突破模拟题（A卷）
（考试时间：100分钟；满分：120分）
一、选一选：（每小题3分，共42分）
1. 若代数式在实数范围内有意义，则x的取值范围是（ ）
A. x≥－3 B. x＞3 C. x≥3 D. x≤3
2. 下列计算错误的是（　　）
A. B. C. D.
3. 顺次连接矩形四边中点所得的四边形一定是（ ）
A. 正方形 B. 矩形 C. 菱形 D. 等腰梯形
4. 若关于的方程（k为常数）有两个相等的实数根，则的值为（　　）
A. ﹣4 B. 4 C. ﹣ D.
5. 如图所示，若△ABC∽△DEF，则∠E度数为（　　）

A. 28° B. 32° C. 42° D. 52°
6. 如图，将△ABC沿DE翻折，折痕DE∥BC，若，BC=9 ，则DE的长等于（　　）

A. 2 B. 3 C. 4 D. 4.5
7. 如图，修建抽水站时，沿着坡度为i=1： 的斜坡铺设水管．若测得水管A处铅垂高度为8 m，则所铺设水管AC的长度为（   ）

A. 8m B. 12m C. 14m D. 16m
8. 将一元二次方程x2-4x-6=0化成（x-a）2=b的形式，则b等于（　　）
A. 4 B. 6 C. 8 D. 10
9. 如图，铁路路基横断面为一个等腰梯形，若腰的坡度为i=3：2，顶宽是7米，路基高是6米，则路基的下底宽是（　　）

A. 7米 B. 11米 C. 15米 D. 17米
10. 如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端25米的B处，测得树顶A的仰角∠ABO为a，则树0A的高度为( )

A. 米 B. 25sina米 C. 25tana米 D. 25cosa米
11. 参加足球联赛的每两队之间都进行一场比赛，共有比赛55场，总共有（　　）支球队参加比赛．
A. 9 B. 10 C. 11 D. 12
12. 某班为迎接“体育健康周”，从3 名学生（1男 2女）中随机选两名担任入场式旗手，则选中两名女学生的概率是（　　）
A. B. C. D.
13. 如图，在Rt△ABC中，∠C=90°，∠CAB平分线交BC于D，DE是AB的垂直平分线，垂足为E，若BC=3，则DE的长为（　　）

A. 1 B. 2 C. 3 D. 4
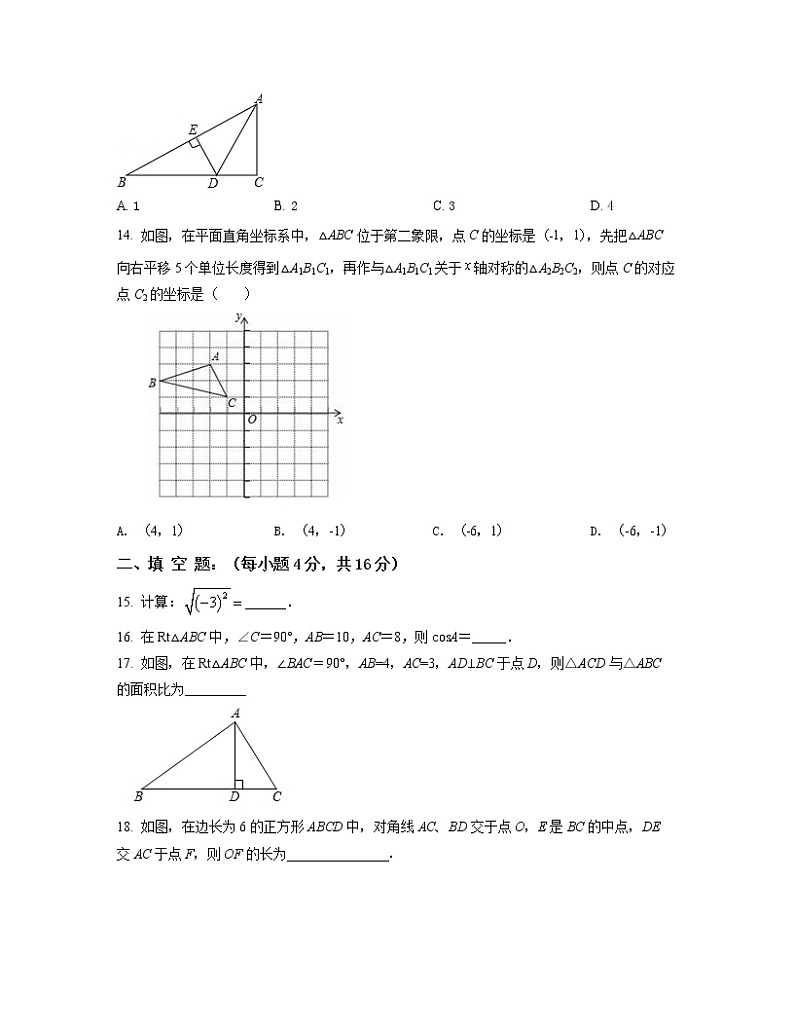
14. 如图，在平面直角坐标系中，△ABC位于第二象限，点C的坐标是（﹣1，1），先把△ABC向右平移5个单位长度得到△A1B1C1，再作与△A1B1C1关于轴对称的△A2B2C2，则点C的对应点C2的坐标是（　　）

A. （4，1） B. （4，-1） C. （﹣6，1） D. （-6，-1）
二、填 空 题：（每小题4分，共16分）
15. 计算：______．
16. 在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则cosA＝_____．
17. 如图，在Rt△ABC中，∠BAC＝90°，AB=4，AC=3，AD⊥BC于点D，则△ACD与△ABC的面积比为_________

18. 如图，在边长为6的正方形ABCD中，对角线AC、BD交于点O，E是BC的中点，DE交AC于点F，则OF的长为_______________．

三、解 答 题：（共62分）
19. 计算：
（1） ；（2）；（3）（1-cos60°）2+.
20. 如图，在Rt△ABC中，∠ABC＝90°，BD⊥AC于点D ，点E为线段BC的中点，AD＝2，tan A＝2．
（1）求AB长；
（2）求DE的长．

21. 初三某班从A、B、C、D四位同学中选出两名同学去参加学校的羽毛球双打比赛．
（1）请用树状图法，求恰好选中A、C两位同学的概率；
（2）若已确定B被选中，再从其余三位同学中随机选取一位，求恰好选中C同学的概率．
22. 如图，在平面直角坐标系中，△ABC三个顶点坐标分别为A（-1，3），B（-2，1），C（-3，1）．
（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1点的坐标及sin∠B1C1A1的值；
（2）以原点O为位似，位似比为1：2，在y轴左侧，画出将△ABC放大后的△A2B2C2，并写出A2点的坐标；
（3）若点D为线段BC的中点，直接写出（2）的变化后点D的对应点D2的坐标．

23. 如图，为了求某条河的宽度，在它的对岸岸边任意取一点A，再在河的这边沿河边取两点B、C，使得∠ABC=45°，∠ACB=30°，量得BC的长为40m，求河的宽度（结果保留根号）．

24. 如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以5cm/s的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以4cm/s的速度向点B匀速运动，运动时间为t s（0＜t＜2），连接PQ．

（1）若△BPQ和△ABC相似，求t的值；
（2）连接AQ，CP，若AQ⊥CP，求t的值．





2022-2023学年贵州省遵义市九年级上册数学期末专项突破模拟题（A卷）
（考试时间：100分钟；满分：120分）
一、选一选：（每小题3分，共42分）
1. 若代数式在实数范围内有意义，则x的取值范围是（ ）
A. x≥－3 B. x＞3 C. x≥3 D. x≤3
【正确答案】C

【详解】由题意得x－3≥0，即x≥3;
故当x≥3时，在实数范围内有意义;
故选C．
2. 下列计算错误的是（　　）
A. B. C. D.
【正确答案】B

【详解】A.，正确；
B.，无法计算，错误；
C.，正确；
D.，正确；
故选B.
3. 顺次连接矩形四边中点所得的四边形一定是（ ）
A. 正方形 B. 矩形 C. 菱形 D. 等腰梯形
【正确答案】C

【分析】矩形的性质，三角形中位线定理，菱形的判定．
【详解】解：如图，连接AC、BD

在△ABD中，∵AH=HD，AE=EB
∴EH=BD
同理FG=BD，HG=AC，EF=AC
又∵在矩形ABCD中，AC=BD
∴EH=HG=GF=FE
∴四边形EFGH菱形
故选C．
4. 若关于的方程（k为常数）有两个相等的实数根，则的值为（　　）
A. ﹣4 B. 4 C. ﹣ D.
【正确答案】C

【详解】根据方程x2-x-k=0有两个相等的实数根，则根的判别式△=b2-4ac=0，从而可以建立关于k的方程，解之即可求出k的值．
解：∵方程有两个相等的实数根，
∴△=b2−4ac=（-1）2+4k=0，
解得：k=﹣，
故选C
5. 如图所示，若△ABC∽△DEF，则∠E的度数为（　　）

A. 28° B. 32° C. 42° D. 52°
【正确答案】C

【详解】∵△ABC∽△DEF，
∴∠B=∠E，
在△ABC中，∠A=110°，∠C=28°，
∴∠B=180°-∠A-∠C=42°，
∴∠E=42°，
故选C．
6. 如图，将△ABC沿DE翻折，折痕DE∥BC，若，BC=9 ，则DE的长等于（　　）

A. 2 B. 3 C. 4 D. 4.5
【正确答案】B

【分析】延长BD和CE交于A′，求出△A′DE∽△A′BC，得出比例式，代入求出即可．
【详解】解：延长BD和CE交于A′，

∵将△ABC沿DE翻折，折痕DE∥BC，，
，
即，
∵DE∥BC，
∴△A′DE∽△A′BC，
，
，
即DE=3，
故选：B．
7. 如图，修建抽水站时，沿着坡度为i=1： 的斜坡铺设水管．若测得水管A处铅垂高度为8 m，则所铺设水管AC的长度为（   ）

A. 8m B. 12m C. 14m D. 16m
【正确答案】D

【详解】首先根据坡度的定义求出BC的长度，然后根据勾股定理求出AC的长度．
解；∵该斜坡的坡度为i=1: ，
∴AB:BC=1:，
∵AB=8m，
∴BC=8m，
则AC=m.
故选D.
8. 将一元二次方程x2-4x-6=0化成（x-a）2=b的形式，则b等于（　　）
A. 4 B. 6 C. 8 D. 10
【正确答案】D

【详解】利用配方法即可得出答案.
解：∵，
，
，
，
∴b＝10.
故选D.
9. 如图，铁路路基横断面为一个等腰梯形，若腰的坡度为i=3：2，顶宽是7米，路基高是6米，则路基的下底宽是（　　）

A. 7米 B. 11米 C. 15米 D. 17米
【正确答案】C

【详解】可过上底的两个端点，分别作下底的垂线段，根据腰的坡度和梯形的高求出下底的长．
解：如图所示 ，等腰梯形ABCD是铁路路基的横断面，腰AB、CD的坡度为3: 2，BC=7米，BE=CF=6米.

在Rt△ABE中,
tanA=，BE=6米，
∴AE==4米，
∴DF=AE=4米，
∴AD=AE+EF+FD=AE+BC+FD=4+7+4=15(米).
故选C.
10. 如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端25米的B处，测得树顶A的仰角∠ABO为a，则树0A的高度为( )

A. 米 B. 25sina米 C. 25tana米 D. 25cosa米
【正确答案】C

【详解】首先根据题意可知，在Rt△ABO中，BO=25米，∠ABO为，正切函数的定义得：tan=，接下来再代值进行计算，即可求得树高OA的长.
解：在Rt△ABO中，
∵BO=25米，∠ABO为，
∴AO=BO·tan=25tan（米）.
故选C.
点睛：本题主要考查了解直角三角形的知识，熟练掌握锐角三角函数的定义是解决本题的关键.
11. 参加足球联赛的每两队之间都进行一场比赛，共有比赛55场，总共有（　　）支球队参加比赛．
A. 9 B. 10 C. 11 D. 12
【正确答案】C

【分析】每个队都要与其余队比赛一场，而两队之间只赛1场．所以等量关系为：队的个数×（队的个数-1）×=55，把相关数值代入计算即可．
【详解】设有x队参加比赛.
x(x−1)=55，
(x−11)(x+10)=0，
解得x1=11，x2=−10(没有合题意，舍去).
故选C.
12. 某班为迎接“体育健康周”，从3 名学生（1男 2女）中随机选两名担任入场式旗手，则选中两名女学生的概率是（　　）
A. B. C. D.
【正确答案】A

【详解】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好选中两名女学生的情况，再利用概率公式即可求得答案．
解：画树状图得：

∵共有6种等可能的结果，恰好选中两名女学生的有2种情况，
∴恰好选中两名女学生的概率是.
故选A.
13. 如图，在Rt△ABC中，∠C=90°，∠CAB的平分线交BC于D，DE是AB的垂直平分线，垂足为E，若BC=3，则DE的长为（　　）

A. 1 B. 2 C. 3 D. 4
【正确答案】A

【详解】试题分析：由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°，∵DE垂直平分AB，
∴DA=DB，∴∠B=∠DAB，∵AD平分∠CAB，∴∠CAD=∠DAB， ∵∠C=90°，∴3∠CAD=90°，
∴∠CAD=30°， ∵AD平分∠CAB，DE⊥AB，CD⊥AC， ∴CD=DE=BD， ∵BC=3， ∴CD=DE=1
考点：线段垂直平分线的性质
14. 如图，在平面直角坐标系中，△ABC位于第二象限，点C的坐标是（﹣1，1），先把△ABC向右平移5个单位长度得到△A1B1C1，再作与△A1B1C1关于轴对称的△A2B2C2，则点C的对应点C2的坐标是（　　）

A. （4，1） B. （4，-1） C. （﹣6，1） D. （-6，-1）
【正确答案】B

【详解】首先利用平移的性质得到△A1B1C1，进而利用关于x轴对称点的性质得到△A2B2C2，即可得出答案．
解：如图所示：点C的对应点C2的坐标是：(4,−1).

故选B.
二、填 空 题：（每小题4分，共16分）
15. 计算：______．
【正确答案】3

【分析】根据算术平方根的定义求解即可．
【详解】解：，
故3．
本题考查了算术平方根，熟练掌握算术平方根的定义是解答本题的关键， 正数有一个正的算术平方根，0的平方根是0，负数没有算术平方根．
16. 在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则cosA＝_____．
【正确答案】

【分析】根据勾股定理求出边BC的长，利用余弦定理cosA=即可解得．
【详解】Rt△ABC中，∠C＝90°，AB＝10，AC＝8，所以BC==6,所以cosA===.
本题考查勾股定理以及余弦定理．
17. 如图，在Rt△ABC中，∠BAC＝90°，AB=4，AC=3，AD⊥BC于点D，则△ACD与△ABC的面积比为_________

【正确答案】9：25

【详解】根据题意先通过勾股定理求出BC的长，再利用两角相等的两个三角形相似来证明△CAD∽△CBA，从而得出相似比为3：5，再根据两相似三角形的面积比等于相似比的平方即可得出答案．
解：在Rt△ABC中，∠BAC＝90°，AB=4，AC=3，
∴BC＝，
在△CAD和△CBA中，
∵∠C=∠C, ∠ADC =∠BAC =90°，
∴△CAD∽△CBA，
∴△CAD与△CBA相似比为，
∴△CAD与△CBA的面积之比=()2=.
故答案.
18. 如图，在边长为6的正方形ABCD中，对角线AC、BD交于点O，E是BC的中点，DE交AC于点F，则OF的长为_______________．

【正确答案】

【详解】过点E作EG⊥BD于点G，可得△BEG是等腰直角三角形，再证△DOF∽△DGE，根据相似的性质即可求出答案.
解：过点E作EG⊥BD于点G，

∵四边形ABCD是正方形，
∴∠GBE=45°，
∴△BEG是等腰直角三角形.
∵BE＝BC＝3，
∴，
∵BD=,
∴DO=，DE=-=,
∵∠DOF=∠DGE =90°，∠ODF=∠GDE，
∴△DOF∽△DGE，
∴
即，
∴.
故答案为.
点睛：本题主要考查正方形的性质和相似的性质. 利用辅助线构造相似三角形是解题的关键.
三、解 答 题：（共62分）
19. 计算：
（1） ；（2）；（3）（1-cos60°）2+.
【正确答案】（1）；（2）；（3）．

【详解】（1）（2）利用二次根式的性质及运算法则进行计算即可；
（3）先求角的三角函数值，再按混合运算顺序进行计算即可.
解：（1）原式＝，
＝，
＝；
（2）原式＝，
＝；
（3）原式＝，
＝.
20. 如图，在Rt△ABC中，∠ABC＝90°，BD⊥AC于点D ，点E为线段BC的中点，AD＝2，tan A＝2．
（1）求AB的长；
（2）求DE的长．

【正确答案】（1）AB＝；（2）DE＝．

【分析】（1）利用∠A的正切值求出BD的长，再利用勾股定理即可求出AB；
（2）利用∠A的正切值求出BC的长，再根据直角三角形斜边上的中线等于斜边的一半即可求出DE的长．
【详解】解：（1）∵BD⊥AC，且tan A＝2．
∴，
∵AD＝2，
∴BD＝4，
∴AB＝；
（2）在Rt△ABC中，
∵∠ABC＝90°，且tan A＝2．
∴，
∵AB＝，
∴BC＝，
∵BD⊥AC，且E点为线段BC的中点，
∴DE＝BC＝.
21. 初三某班从A、B、C、D四位同学中选出两名同学去参加学校羽毛球双打比赛．
（1）请用树状图法，求恰好选中A、C两位同学的概率；
（2）若已确定B被选中，再从其余三位同学中随机选取一位，求恰好选中C同学的概率．
【正确答案】（1）；（2）.

【详解】（1）根据题意画出树状图，然后由树状图得出所有等可能的结果和恰好符合选中A、C两位同学的情况，再利用概率公式即可求出答案；
（2）根据所有等可能对结果及选中C同学的情况，利用概率公式即可求解.
解：（1）画树状图得，

∵共有12种等可能的结果，恰好选中A、C两位同学的只有2种情况，
∴恰好选中A、C两位同学的概率为：；
（2）∵一共有3种等可能性的结果，其中恰好选中C同学的有1种，
∴恰好选中C同学概率为.
22. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-1，3），B（-2，1），C（-3，1）．
（1）画出△ABC关于y轴对称的△A1B1C1，并写出A1点的坐标及sin∠B1C1A1的值；
（2）以原点O为位似，位似比为1：2，在y轴的左侧，画出将△ABC放大后的△A2B2C2，并写出A2点的坐标；
（3）若点D为线段BC的中点，直接写出（2）的变化后点D的对应点D2的坐标．

【正确答案】（1）A1（1，3），sin∠B1C1A1=；（2）A2（-2，6）；（3）D2（－5，2）．

【分析】（1）利用关于y轴对称点的性质得出对应点坐标进而求出即可；
（2）利用位似图形的性质得出对应点位置即可得出答案；
（3）利用位似比得出对应点坐标的变化规律进而得出答案．
【详解】解：(1)如图,△A1B1C1，即为所求，

∴A1(1,3)，sin∠B1 C1A1=sin45°=；
（2）如图所示,△A2B2C2，即为所求，
∴A2(−2,6)；
（3）∵点D在线段BC的中点上，
∴D（-2.5，1），
∵位似比为1:2，
∴D2(-5，2).
23. 如图，为了求某条河的宽度，在它的对岸岸边任意取一点A，再在河的这边沿河边取两点B、C，使得∠ABC=45°，∠ACB=30°，量得BC的长为40m，求河的宽度（结果保留根号）．

【正确答案】m．

【分析】如图，过A作AD⊥BC于D，设AD=xm，通过锐角三角函数可知：BD＝xm，DC＝xm；根据BC的长为40m即可建立方程，解之即可求出河宽.
【详解】解：作AD⊥BC,垂足为D.

设AD= xm，
∵∠ABC=45°，
∴BD＝AD= xm，
∵∠ACB=30°，
∴DC＝＝xm，
∵AD+DC=BC ,且BC＝40m，
∴，
解得，，
答：则河的宽度为m.
本题主要考查解直角三角形的实际应用. 通过添加辅助线构造直角三角形是解题的关键.
24. 如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm，动点P从点B出发，在BA边上以5cm/s的速度向点A匀速运动，同时动点Q从点C出发，在CB边上以4cm/s的速度向点B匀速运动，运动时间为t s（0＜t＜2），连接PQ．

（1）若△BPQ和△ABC相似，求t的值；
（2）连接AQ，CP，若AQ⊥CP，求t的值．
【正确答案】（1）t的值为1s或s；（2）t的值为s．

【分析】（1）根据勾股定理即可得到结论；分两种情况：①当△BPQ∽△BAC时，②当△BPQ∽△BCA时，根据相似三角形的性质，把BP=5t，QC=4t，AB=10cm，BC=8cm，代入计算即可；
（2）过P作PM⊥BC于点M，AQ，CP交于点N，则有PB=5t，PM=3t，MC=8-4t，根据△ACQ∽△CMP，得出AC：CM=CQ：MP，代入计算即可．
【详解】解：（1）∵∠ACB=90°，AC=6cm，BC=8cm，
∴AB==10（cm），
分两种情况讨论：
①当△BPQ∽△BAC时，，
∵BP=5t，QC=4t，AB=10，BC=8，
∴，
解得，t=1，
②当△BPQ∽△BCA时，，
∴，
解得，t=，
∴t=1s或s时，△BPQ∽△BCA；
（2）过P作PM⊥BC于点M，AQ，CP交于点N，如图所示，

则PB=5t，MC=8-4t，
∵PM⊥BC，∠ACB=90°，
∴PM∥AC，
∴△BPM∽△BAC，
∴，即，
∴PM=3t，BM=4t，MC=8-4t，
∵∠NAC+∠NCA=90°，∠PCM+∠NCA=90°，
∴∠NAC=∠PCM，
∵∠ACQ=∠PMC，
∴△ACQ∽△CMP，
∴，
∴，
解得t=．
本题考查了相似三角形的判定与性质，勾股定理，直角三角形的性质，由三角形相似得出对应边成比例是解题的关键．




2022-2023学年贵州省遵义市九年级上册数学期末专项突破模拟题（B卷）
一、选一选(本题共12小题，每题3分，共36分）
1. 下列图形中既是对称图形又是轴对称图形的是( )
A B. C. D.
2. 已知关于x一元二次方程的一个根为1，则m的值为( )
A. 1 B. -8 C. -7 D. 7
3. 将抛物线向左平移2单位，再向上平移3个单位，则所得的抛物线解析式为（ ）
A. B. C. D.
4. 一个没有透明的袋子中有3个红球和2个黄球，这些球除颜色外完全相同．从袋子中随机摸出一个球，它是黄球的概率为（ ）
A. B. C. D.
5. 一元二次方程的根的情况是（ ）
A. 有两个没有相等的实根 B. 有两个相等的实根
C. 无实数根 D. 没有能确定
6. 若抛物线与y轴的交点为，则下列说法没有正确的是（ ）
A. 抛物线开口向上 B. 抛物线与轴的交点为
C. 抛物线对称轴是 D. 当时,y有值-4
7. 下列正多边形中，绕其旋转72°后，能和自身重合的是（ ）
A. 正方形 B. 正五边形
C. 正六边形 D. 正八边形
8. 如图，已知点A，B，C在⊙O上，∠ACB=50°，则∠AOB的度数为（ ）

A. 50° B. 100° C. 25° D. 70°
9. 如图，⊙O的半径为1cm，正六边形内接于⊙O，则图中阴影部分面积为（ ）

A. B. C. D.
10. 某机械厂4月份生产零件80万个，第二季度生产零件160万个.设该厂五、六月份平均每月增长率为，那么满足的方程是（ ）
A. B.
C. D.
11. 已知反比例函数和直线在同一坐标系内的图象如图所示，其中正确的是（ ）

A. ①② B. ③④ C. ①③ D. ②④
12. 一项“过关游戏”规定：在过第n关时要将一颗质地均匀的骰子（六个面上分别刻有1到6的点数）抛掷n次，若n次抛掷所出现的点数之和大于n2，则算过关；否则没有算过关，则能过第二关的概率是（ ）
A. B. C. D.
二、填 空 题（本大题共6小题，每题4分，共24分）
13. 写出点（-1，1）的反比例函数的解析式________．
14. 如图，以点O为旋转，将△ABO按顺时针方向旋转100°得到△DOF，若∠AOB=40°， 则∠DOB为______度．

15. 有一圆锥，它的高为8cm，底面半径为6cm，则这个圆锥的侧面积是________cm2．（结果保留π）
16. 如图，⊙O的直径CD＝10，弦AB＝8，AB⊥CD，垂足为M，则DM的长为_____．

17. 如图，在4×4正方形网格中，任选取一个白色的小正方形并涂黑，使图中黑色部分的图形构成一个轴对称图形的概率是______．

18. 已知二次函数的图像如图所示，下列4个结论：①；②；③；④．其中正确的结论有__________．

三、解 答 题（本大题共9小题，共90分）
19. △ABC三个顶点A，B，C在平面直角坐标系中位置如图所示．将△ABC绕C点顺时针旋转90°，画出旋转后的△A2B2C2，并写出A2，B2的坐标．

20. （1） (2)
21. 如图所示，在⊙O中直径AB垂直于弦CD，垂足为E，若BE=2cm，CD=6cm．求⊙O的半径．

22. 如图，函数y＝－x与函数y＝－的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D，则四边形ACBD的面积________．

23. 如图，在Rt△ADC中，∠ADC＝90°，以CD为直径的⊙O交AC于点E，点G是AD的中点．
求证：GE是⊙O的切线．

24. 一没有透明布袋里，装有红、黄、蓝三种颜色的小球（除颜色外其余都相同），其中有红球2个，蓝球1个，黄球若干个，现从中任意摸出一个球是红球的概率为．
（1）求口袋中黄球的个数；
（2）甲同学先随机摸出一个小球（没有放回），再随机摸出一个小球，请用“树状图法”或“列表法”，求两次摸出都是红球的概率；
25. 函数与反比列函数的图像交于A（-2，1），B（1，)两点，求△ABO的面积．

26. 某市场一批衬衫，平均每天可20件，每件赢利40元．了扩大，增加赢利，尽快减少库存，商场决定采取适当降价措施．经发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．求：
（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？
（2）要使商场平均每天赢利至多，请你帮助设计．
27. 如图，抛物线与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴为=–1，P为抛物线上第二象限的一个动点．
（1）求抛物线的解析式并写出其顶点坐标；
（2）当点P的纵坐标为2时，求点P的横坐标；
（3）当点P在运动过程中，求四边形PABC面积时值及此时点P的坐标．



2022-2023学年贵州省遵义市九年级上册数学期末专项突破模拟题（B卷）
一、选一选(本题共12小题，每题3分，共36分）
1. 下列图形中既是对称图形又是轴对称图形的是( )
A. B. C. D.
【正确答案】C

【分析】根据轴对称图形和对称图形的概念，对各个选项进行判断，即可得到答案.
【详解】解：A、是轴对称图形，没有是对称图形，故A错误；
B、是轴对称图形，没有是对称图形，故B错误；
C、既是轴对称图形，也是对称图形，故C正确；
D、既没有是轴对称图形，也没有是对称图形，故D错误；
故选：C.
本题考查了轴对称图形和对称图形的概念，解题的关键是熟练掌握概念进行分析判断.
2. 已知关于x的一元二次方程的一个根为1，则m的值为( )
A. 1 B. -8 C. -7 D. 7
【正确答案】D

【分析】直接利用一元二次方程的解的意义将x=1代入求出答案即可．
【详解】∵关于x的一元二次方程x2+mx−8=0的一个根是1，
∴1+m−8=0，
解得：m=7.
故答案选：D.
本题考查的知识点是一元二次方程的解，解题的关键是熟练的掌握一元二次方程的解.
3. 将抛物线向左平移2单位，再向上平移3个单位，则所得的抛物线解析式为（ ）
A. B. C. D.
【正确答案】A

【分析】根据抛物线平移规律“左加右减，上加下减”，写出平移后的抛物线解析式，再选择即可．
【详解】抛物线向左平移2单位，再向上平移3单位后的抛物线解析式为：．
故选：A．
本题考查抛物线的平移，掌握抛物线平移规律是解题的关键．
4. 一个没有透明的袋子中有3个红球和2个黄球，这些球除颜色外完全相同．从袋子中随机摸出一个球，它是黄球的概率为（ ）
A. B. C. D.
【正确答案】B

【分析】根据概率的求法，找准两点：①全部等可能情况的总数；②符合条件的情况数目；二者的比值就是其发生的概率．
【详解】解：∵袋子中球的总数为：2+3=5，有2个黄球，
∴从袋子中随机摸出一个球，它是黄球的概率为：．
故选B．
5. 一元二次方程的根的情况是（ ）
A. 有两个没有相等的实根 B. 有两个相等的实根
C. 无实数根 D. 没有能确定
【正确答案】C

【详解】∵△=(-3)2-4×1×4=9-16=-70时，一元二次方程有两个没有相等的实数根；当△=0时，一元二次方程有两个相等的实数根；当△