北师大版九年级下册1 锐角三角函数示范课ppt课件

这是一份北师大版九年级下册1 锐角三角函数示范课ppt课件，共24页。PPT课件主要包含了生活中的梯子，陡意味着倾斜程度大，铅直高度，水平宽度，相关概念，一样陡，倾斜角的对边，倾斜角的邻边，想一想，比值不变等内容，欢迎下载使用。

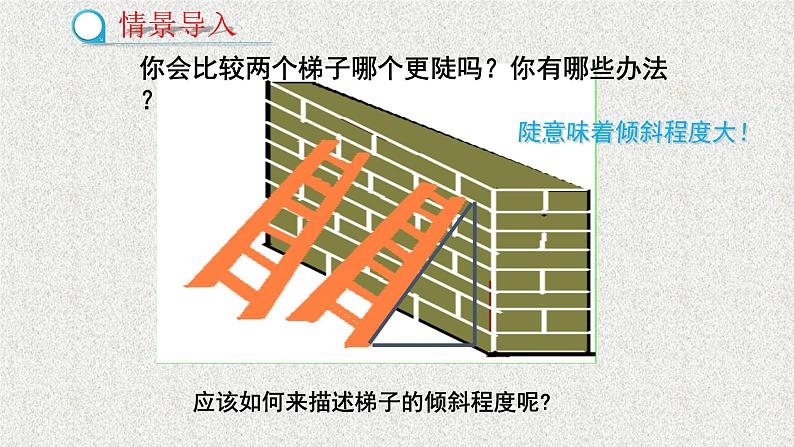
梯子是我们日常生活中常见的物体.
你会比较两个梯子哪个更陡吗？你有哪些办法？
应该如何来描述梯子的倾斜程度呢?
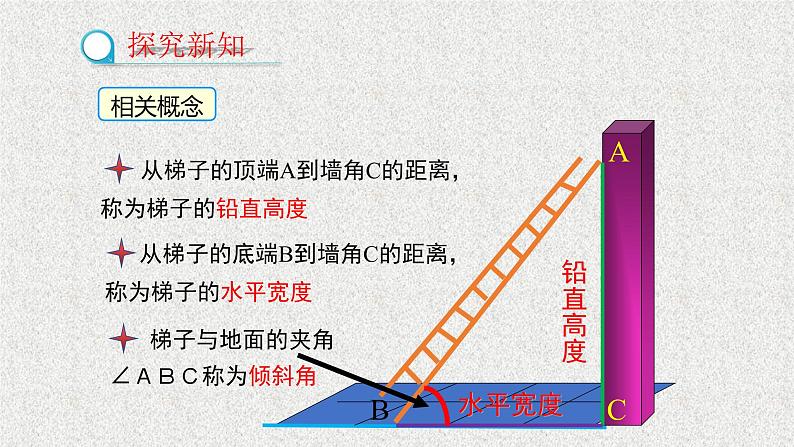
梯子与地面的夹角∠ＡＢＣ称为倾斜角
从梯子的顶端A到墙角C的距离，称为梯子的铅直高度
从梯子的底端B到墙角C的距离，称为梯子的水平宽度
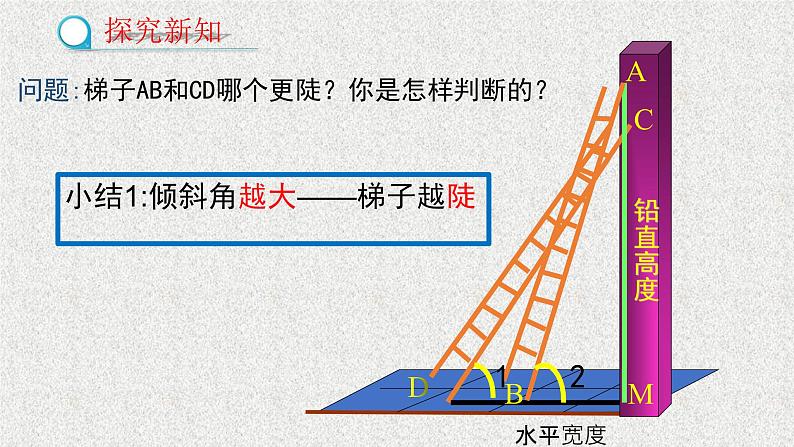
小结1:倾斜角越大——梯子越陡
问题:梯子AB和CD哪个更陡？你是怎样判断的？
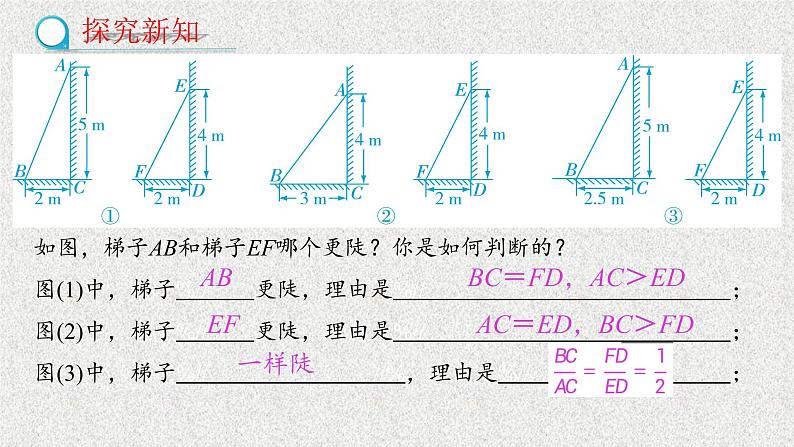
如图，梯子AB和梯子EF哪个更陡？你是如何判断的？图(1)中，梯子%//更陡，理由是%//；图(2)中，梯子%//更陡，理由是%//；图(3)中，梯子%////%，理由是%//；
AC＝ED，BC＞FD
BC＝FD，AC＞ED
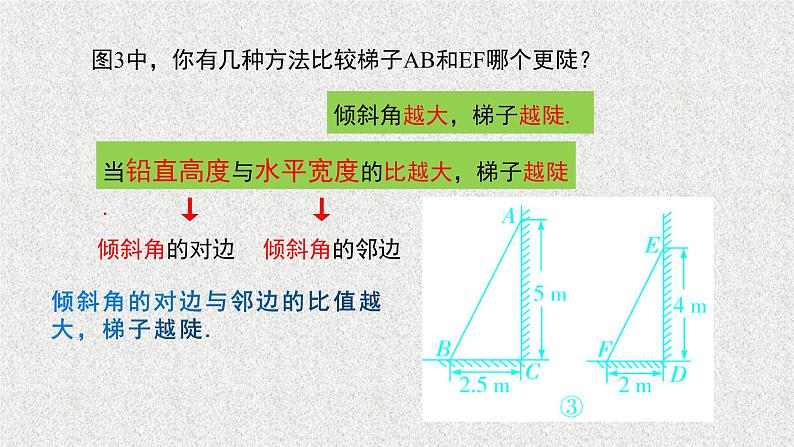
图3中，你有几种方法比较梯子AB和EF哪个更陡？
当铅直高度与水平宽度的比越大，梯子越陡.
倾斜角越大，梯子越陡.
倾斜角的对边与邻边的比值越大，梯子越陡.
判断梯子是否更陡，有如下方法：
1.可以利用倾斜角的大小比较，倾斜角越大，梯子越陡. 2.可以利用倾斜角的对边与邻边的比值大小来判断，比值越大，梯子越陡.
例2.若小明因身高原因不能顺利测量梯子顶端到墙脚的距离B1 C1 ,进而无法刻画梯子的倾斜程度，他该怎么办？你有什么锦囊妙计？
(1)Rt△AB1C1和Rt△AB2C2有什么关系?
Rt△AB1C1∽Rt△AB2C2
∵Rt△AB1C1∽Rt△AB2C2
(3)如果改变B2在梯子上的位置(如B3C3 )呢?
思考：由此你得出什么结论?
当直角三角形中的锐角确定之后，它的对边与邻边之比也随之确定．
我们把∠A的对边与∠A的邻边的比，叫做∠A的////%/(tangent)，记作%////%，即
请同学们思考，梯子的倾斜程度与tanA(倾斜角∠A的正切)的值有关吗？关系是：%//_______\
tanA的值越大，梯子越陡
1.下图表示甲、乙两个自动扶梯,哪一个自动扶梯比较陡?
∵ tanα> tanβ∴甲梯更陡
有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度 (即tanα)就是:
坡角：坡面与水平面的夹角α称为坡角；坡度i（也叫坡比）：坡面的铅直高度与水平宽度的比称为坡度(或坡比) 即坡度等于坡角的正切.
坡角越大，坡度越大，坡面就越陡.
例3 如图，梯形护坡石坝的斜坡AB的坡度i =1∶3，坝高BC＝2米，则斜坡AB的长是(　　)
解析：∵∠ACB＝90°，坡度i =1∶3，
方法总结：坡度等于坡角的正切.理解坡度的概念是解决与坡度有关的计算题的关键．
∵BC＝2米，∴AC＝3BC＝3×2＝6(米)．
例4. 如图，拦河坝的横断面为梯形ABCD，斜坡AB的坡度为2:3，坝高BE＝4 m，坝顶BC＝3 m，斜坡CD＝5 m．(1)比较斜坡AB和CD哪个更陡；(2)求坝底AD的长．
(2)∵BC＝3米，∴FE的长为3米，∵斜坡AB的坡度为2:3，∴AE＝6，∴AD＝6＋3＋3＝12m．
∠A越大，tanA越大,梯子越陡
1. 在Rt△ABC中，∠C=90°，AC=7，BC=5，则 tan A=______，tan B =______．
互余两锐角的正切值互为倒数.
(1) 在Rt△ABC中∠C=90°，BC=5, AB=13, tanA= , tanB= .
(2)在Rt△ABC中∠C=90°，BC=5,tanA= , AC= .
3.如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA= （ ）
A. B.C. D.
4.如图，在△ABC中，AC＝AB＝10，BC＝16，则tanB＝%////%．