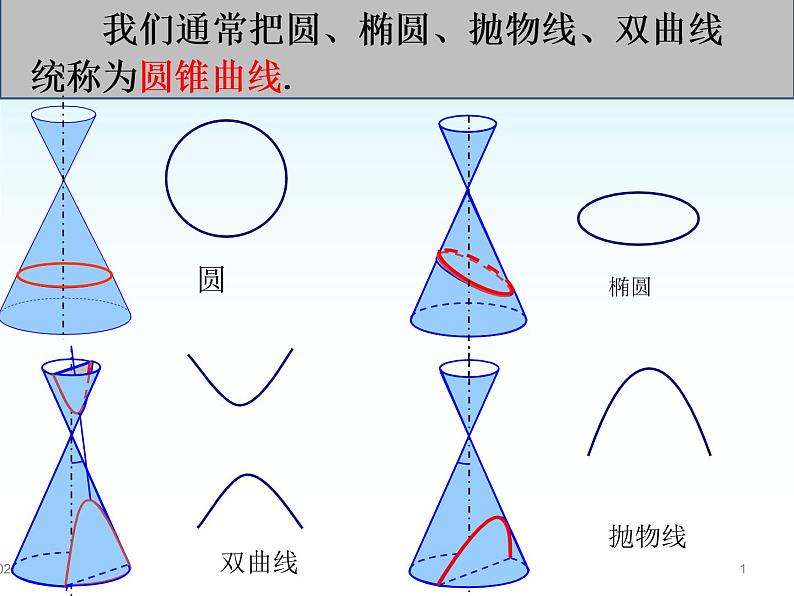
选择性必修 第一册第三章 圆锥曲线的方程3.1 椭圆集体备课课件ppt

这是一份选择性必修 第一册第三章 圆锥曲线的方程3.1 椭圆集体备课课件ppt，共44页。PPT课件主要包含了“传说中的”飞碟，1在平面内，椭圆的定义，步骤三化简方程，求曲线方程的步骤，椭圆方程的建立，方程的推导，椭圆标准方程分析，1形式，定义法等内容，欢迎下载使用。

3.1.1 椭圆及其标准方程
圆:平面内到定点距离等于定长的动点的轨迹.
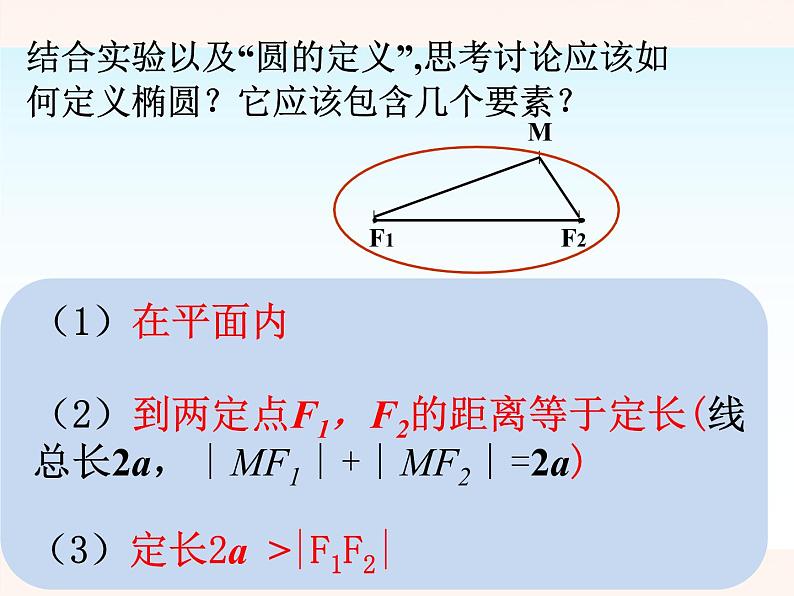
椭圆是满足什么几何条件的点的轨迹呢？
观察并思考下面两个问题：(1)动点运动出的轨迹是什么？(2)动点满足怎样的几何条件？
（2）到两定点F1，F2的距离等于定长(线总长2a，∣MF1∣+∣MF2∣=2a)
（3）定长2a >|F1F2|
结合实验以及“圆的定义”,思考讨论应该如何定义椭圆？它应该包含几个要素？
※当∣MF1∣+∣MF2∣=∣F1F2∣，动点M轨迹为线段
※当∣MF1∣+∣MF2∣<∣F1F2∣，动点M轨迹不存在
说明：※当∣MF1∣+∣MF2∣＞∣F1F2∣，动点M轨迹为椭圆
平面内到两定点F1、F2的距离之和等于常数(2a，大于|F1F2|)的点的轨迹叫做椭圆．
※这两个定点F1，F2叫做椭圆的焦点
※两焦点的距离（∣F1F2∣=2c）叫做焦距
步骤一：建立适当的直角坐标系, 设动点坐标
步骤二：找关系式，列方程
由椭圆的定义, 可知：|MF1|+|MF2|=2a
由两点间的距离公式，可知：
因2a>2c，即a>c，故a2-c2>0，令a2-c2=b2，其中b>0，代入上式, 可得：
两边同时除以a2(a2-c 2) 得：
方程 叫做椭圆的标准方程
※焦点在x轴上※焦点坐标是F1(-c，0)、 F2(c，0)※b2=a2－c2．
如果椭圆的焦点在y轴上，焦点是F1(0,-c)、F2(0,c)．方程是怎样呢？
这个也是椭圆的标准方程
设|F1F2|=2c(c＞0)，M(x，y)为椭圆上任意一点，则有F1(0,-c)，F2(0,c)，
又由椭圆 的定义可得： |MF1|+ |MF2|=2a
椭圆的标准方程的再认识：
（2）三个参数满足a2=b2+c2
（3）椭圆的标准方程中，x2与y2的分母哪一个大，则焦点在哪一个轴上
1.判定下列椭圆的焦点在哪个轴，并指明a2、b2，写出焦点坐标
答：在 x 轴.（-3，0）和（3，0）
答：在 y 轴.（0，-5）和（0，5）
答：在y 轴.（0，-1）和（0，1）
焦点在分母大的那个轴上
从椭圆标准方程判断焦点位置：
哪个分母大，焦点就在哪个轴上
平面内到两个定点的距离之和为常数(大于|F1F2|)的点的轨迹是椭圆.
问题：根据表格比较两种标准方程结构之间的异同？
例1 已知椭圆的两个焦点坐标分别是(-2,0), (2,0), 并且经过点 .求它的标准方程.
解:因为椭圆的焦点在x轴上,所以设它的标准方程为
因此, 所求椭圆的标准方程为
另解:因为椭圆的焦点在x轴上,所以设它的标准方程为:
因此, 所求椭圆的标准方程为:
(3)(方法一)①当椭圆的焦点在x轴上时,
利用待定系数法求椭圆的标准方程:当焦点位置不确定时,可设椭圆方程为mx2+ny2=1(m≠n,m>0,n>0).因为它包括焦点在x轴上(mn)两类情况,所以可以避免分类讨论,从而简化了运算.
【变式训练1】 求适合下列条件的椭圆的标准方程:(1)中心在原点,焦点在坐标轴上,且经过两点(2,0)和(0,1);
在本例中,把“∠F1PF2=60°”改为“∠F1PF2=90°”,其余条件不变,试求△PF1F2的面积.解:在△PF1F2中,|F1F2|2=|PF1|2+|PF2|2,∴25=(|PF1|+|PF2|)2-2|PF1|·|PF2|,由椭圆的定义可知|PF1|+|PF2|=10,
例2 如图，在圆 上任取一点P，过点P作x轴的垂线段PD，D为垂足.当点P在圆上运动时，线段PD的中点M的轨迹是什么？为什么？
解：设点M的坐标为（x,y）,点P的坐标为（x0,y0）,则
因为点P（x0,y0）在圆
把点ｘ0=x，y0=2y代入方程①，得
所以点M的轨迹是一个椭圆.
例3 如图，设点A，B的坐标分别是(-5，0)和(5，0),直线AM,BM相交于点M，且它们的斜率之积是 ,求点M的轨迹方程.
解：设点M的坐标（x,y）,因为点A的坐标是（-5,0）,所以,直线AM的斜率为
化简，得点M的轨迹方程为
反思感悟 利用椭圆定义求动点轨迹方程的三个步骤
忽略椭圆方程中的条件a>b而致误
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?提示:错误的原因是没有注意椭圆的标准方程中a>b这个条件,当a=b时,方程并不表示椭圆.
A.4B.5C.8D.10解析:|PF1|+|PF2|=2a=10.答案:D
A.(±4,0)B.(0,±4)C.(±3,0)D.(0,±3)解析:椭圆的焦点在y轴上,且c=3,故焦点坐标为(0,±3).答案:D
答案:a>0,且a≠1
5.已知B,C是两个定点,|BC|=8,且△ABC的周长为18,求这个三角形顶点A的轨迹方程.解:以过B,C两点的直线为x轴,线段BC的中点为原点,建立平面直角坐标系.由|BC|=8,可知点B(-4,0),C(4,0).由|AB|+|BC|+|AC|=18,得|AB|+|AC|=10>|BC|=8.因此,点A的轨迹是以B,C为焦点的椭圆,这个椭圆上的点与两个焦点的距离之和为2a=10,即a=5,且点A不能在x轴上.由a=5,c=4,得b2=9.