北师大版数学八上第7章 测试卷（2）

这是一份北师大版数学八上第7章 测试卷（2），共20页。试卷主要包含了填空题，选择题，解答题等内容，欢迎下载使用。
第七章 章末测试卷
一、填空题（18分）
1．命题“任意两个直角都相等”的条件是　　，结论是　　，它是　　（真或假）命题．
2．已知，如图，直线AB、CD相交于O，OE平分∠BOD且∠AOE=150°，∠AOC的度数为　　．

3．如图，如果∠B=∠1=∠2=50°，那么∠D=　　．

4．如图，直线l1、l2分别与直线l3、l4相交，∠1与∠3互余，∠3的余角与∠2互补，∠4=125°，则∠3=　　．

5．如图，已知AB∥CD，∠C=75°，∠A=25°，则∠E的度数为　　度．

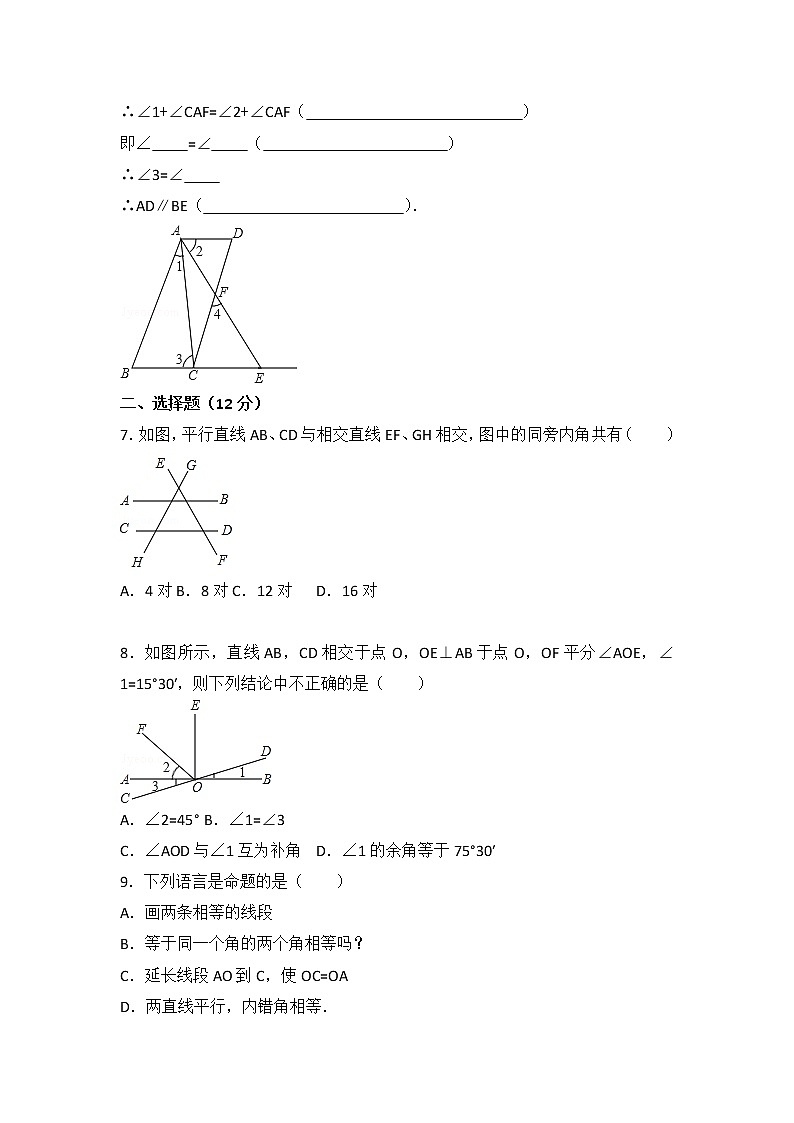
6．如图，AB∥CD，∠1=∠2，∠3=∠4，试说明AD∥BE
解：∵AB∥CD（已知）
∴∠4=∠　 　（　 　）
∵∠3=∠4（已知）
∴∠3=∠　　（　 　）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（　 　）
即∠　 　=∠　 　（　 　）
∴∠3=∠　 　
∴AD∥BE（　 　）．

二、选择题（12分）
7．如图，平行直线AB、CD与相交直线EF、GH相交，图中的同旁内角共有（　　）

A．4对 B．8对 C．12对 D．16对

8．如图所示，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是（　　）

A．∠2=45° B．∠1=∠3
C．∠AOD与∠1互为补角 D．∠1的余角等于75°30′
9．下列语言是命题的是（　　）
A．画两条相等的线段
B．等于同一个角的两个角相等吗？
C．延长线段AO到C，使OC=OA
D．两直线平行，内错角相等．
10．下列命题是假命题的是（　　）
A．对顶角相等 B．﹣4是有理数
C．内错角相等 D．两个等腰直角三角形相似
三、解答题（70分）
11．（4分）已知如图，指出下列推理中的错误，并加以改正．
（1）∵∠1和∠2是内错角，∴∠1=∠2，
（2）∵∠1=∠2，∴AB∥CD（两直线平行，内错角相等）

12．（6分）已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DFE的平分线相交于点P．求证：∠P=90°．

13．（6分）如图，∠1=∠2，∠3=∠4，试问EF是否与GH平行？


14．（6分）如图写出能使AB∥CD成立的各种条件．


15．（6分）如图，已知AB∥CD，∠1=∠3，试说明AC∥BD．


16．（6分）已知：如图，∠1=∠2，且BD平分∠ABC．求证：AB∥CD．


17．（6分）如图，已知直线a，b，c被直线d所截，若∠1=∠2，∠2+∠3=180°，求证：a∥c．


　
18．（6分）如图，已知BE∥CF，BE、CF分别平分∠ABC和∠BCD，求证：AB∥CD．


19．（6分）已知：如图，AB∥CD，BC∥DE，∠B=70°，求∠D的度数．


　
20．（6分）已知：BC∥EF，∠B=∠E，求证：AB∥DE．


21．（6分）如图，已知AB∥CD，∠A=100°，CB平分∠ACD，求∠ACD、∠ABC的度数．


22．（6分）如图，已知：DE⊥AO于点E，BO⊥AO于点O，∠CFB=∠EDO，
证明：CF∥DO．


参考答案
一、填空题（18分）
1．命题“任意两个直角都相等”的条件是　两个角都是直角　，结论是　相等　，它是　真　（真或假）命题．
【考点】命题与定理．
【分析】任何一个命题都是由条件和结论组成．
【解答】解：“任意两个直角都相等”的条件是：两个角是直角，结论是：相等．
它是真命题．
【点评】本题考查了命题的条件和结论的叙述．
　
2．已知，如图，直线AB、CD相交于O，OE平分∠BOD且∠AOE=150°，∠AOC的度数为　60°　．

【考点】对顶角、邻补角；角平分线的定义．
【分析】根据两直线相交，对顶角相等，可推出∠AOC=∠DOB，又根据OE平分∠BOD，∠AOE=150°，可求∠BOE，从而可求∠BOD．
【解答】解：∵AB、CD相交于O，
∴∠AOC与∠DOB是对顶角，即∠AOC=∠DOB，
∵∠AOE=150°，
∴∠BOE=180°﹣∠AOE=30°，
又∵OE平分∠BOD，∠AOE=30°，
∴∠BOD=2∠BOE=2×30°=60°，
∴∠BOD=∠AOC=60°，
故答案为：60°．
【点评】本题主要考查对顶角的性质以及角平分线的定义、邻补角，解决本题的关键是求出∠BOE．
　
3．如图，如果∠B=∠1=∠2=50°，那么∠D=　50°　．

【考点】平行线的判定与性质．
【分析】根据平行线的判定得出AD∥BC，根据平行线的性质得出∠D=∠1，代入求出即可．
【解答】解：∵∠B=∠2=50°，
∴AD∥BC，
∴∠D=∠1，
∵∠1=50°，
∴∠D=50°．
故答案为：50°．
【点评】本题考查了平行线的性质和判定的应用，能推出AD∥BC是解此题的关键．
　
4．如图，直线l1、l2分别与直线l3、l4相交，∠1与∠3互余，∠3的余角与∠2互补，∠4=125°，则∠3=　55°　．

【考点】平行线的判定与性质；余角和补角．
【分析】求出∠5的度数，根据∠1与∠3互余和∠3的余角与∠2互补求出∠1+∠2=180°，根据平行线的判定得出l1∥l2，根据平行线的性质求出即可．
【解答】解：∵∠4=125°，
∴∠5=180°﹣125°=55°，
∵∠1与∠3互余，∠3的余角与∠2互补，
∴∠1+∠2=180°，
∴l1∥l2，
∴∠3=∠5=55°，
故答案为：55°．
【点评】本题考查了平行线的性质和判定的应用，能求出l1∥l2是解此题的关键，注意：两直线平行，内错角相等．
　
5．如图，已知AB∥CD，∠C=75°，∠A=25°，则∠E的度数为　50　度．

【考点】平行线的性质；三角形的外角性质．
【专题】计算题．
【分析】本题主要利用两直线平行，同位角相等和三角形的外角等于与它不相邻的两内角之和作答．
【解答】解：∵AB∥CD，
∴∠BFE=∠C=75°，
又∠A=25°，
∴∠E=75°﹣∠A=50°．
【点评】本题重点考查了平行线的性质及三角形的外角性质，是一道较为简单的题目．
　
6．如图，AB∥CD，∠1=∠2，∠3=∠4，试说明AD∥BE
解：∵AB∥CD（已知）
∴∠4=∠　EAB　（　两直线平行，同位角相等　）
∵∠3=∠4（已知）
∴∠3=∠　EAB　（　等量代换　）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（　等式的性质　）
即∠　BAE　=∠　CAD　（　角的和差　）
∴∠3=∠　CAD　
∴AD∥BE（　内错角相等，两直线平行　）．

【考点】平行线的判定与性质．
【专题】推理填空题．
【分析】由平行线的性质可得到∠4=∠EAB，由∠3=∠4可得到∠3=∠EAB，由等式的性质可知∠BAE=∠CAD，从而得到∠3=∠CAD由平行线的判定定理可得到AD∥BE．
【解答】解：∵AB∥CD（已知）
∴∠4=∠EAB（两直线平行，同位角相等）
∵∠3=∠4（已知）
∴∠3=∠EAB（等量代换）
∵∠1=∠2（已知）
∴∠1+∠CAF=∠2+∠CAF（等式的性质）．
即∠BAE=∠CAD（角的和差）
∴∠3=∠CAD．
∴AD∥BE （内错角相等，两直线平行）．
【点评】本题主要考查的是平行线的性质和平行线的判定，掌握平行线的性质和判定定理是解题的关键．
　
二、选择题（12分）
7．如图，平行直线AB、CD与相交直线EF、GH相交，图中的同旁内角共有（　　）

A．4对 B．8对 C．12对 D．16对
【考点】同位角、内错角、同旁内角．
【专题】几何图形问题．
【分析】每一个“三线八角”基本图形都有两对同旁内角，从对原图形进行分解入手可知同旁内角共有对数．
【解答】解：直线AB、CD被EF所截有2对同旁内角；
直线AB、CD被GH所截有2对同旁内角；
直线CD、EF被GH所截有2对同旁内角；
直线CD、GH被EF所截有2对同旁内角；
直线GH、EF被CD所截有2对同旁内角；
直线AB、EF被GH所截有2对同旁内角；
直线AB、GH被EF所截有2对同旁内角；
直线EF、GH被AB所截有2对同旁内角．
共有16对同旁内角．
故选D．
【点评】本题考查了同旁内角的定义．注意在截线的同旁找同旁内角．要结合图形，熟记同旁内角的位置特点．两条直线被第三条直线所截所形成的八个角中，有两对同旁内角．
　
8．如图所示，直线AB，CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是（　　）

A．∠2=45° B．∠1=∠3
C．∠AOD与∠1互为补角 D．∠1的余角等于75°30′
【考点】垂线；角平分线的定义；对顶角、邻补角．
【分析】根据角平分线性质、对顶角性质、互余、互补角的定义，逐一判断．
【解答】解：A、由OE⊥AB，可知∠AOE=90°，OF平分∠AOE，则∠2=45°，正确；
B、∠1与∠3互为对顶角，因而相等，正确；
C、∠AOD与∠1互为邻补角，正确；
D、∵∠1+75°30′=15°30′+75°30′=91°，
∴∠1的余角等于75°30′，不成立．
故选D．
【点评】本题主要考查邻补角以及对顶角的概念，和为180°的两角互补，和为90°的两角互余．
　
9．下列语言是命题的是（　　）
A．画两条相等的线段
B．等于同一个角的两个角相等吗？
C．延长线段AO到C，使OC=OA
D．两直线平行，内错角相等．
【考点】命题与定理．
【分析】根据命题的定义解答，命题是对事情做出正确或不正确的判断的句子叫做命题，分别判断得出答案即可．
【解答】解：根据命题的定义：
只有答案D、两直线平行，内错角相等．对事情做出正确或不正确的判断，故此选项正确；
故选：D．
【点评】本题考查了命题的定义，利用定义得出是解题关键．
　
10．下列命题是假命题的是（　　）
A．对顶角相等 B．﹣4是有理数
C．内错角相等 D．两个等腰直角三角形相似
【考点】命题与定理．
【分析】根据对顶角的性质对A进行判断；根据有理数的分类对B进行判断；根据平行线的性质对C进行判断；根据等腰直角三角形的性质和相似的判定方法对D进行判断．
【解答】解：A、对顶角相等，所以A选项的命题为真命题；
B、﹣4是有理数，所以B选项的命题为真命题；
C、两直线平行，内错角相等，所以C选项的命题为假命题；
D、两个等腰直角三角形相似，所以D选项的命题为真命题．
故选C．
【点评】本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
　
三、解答题（70分）
11．（4分）已知如图，指出下列推理中的错误，并加以改正．
（1）∵∠1和∠2是内错角，∴∠1=∠2，
（2）∵∠1=∠2，∴AB∥CD（两直线平行，内错角相等）

【考点】平行线的判定．
【分析】（1）内错角不一定相等，只有在平行线中才能推出相等；
（2）根据平行线的判定得出此推理正确．
【解答】解：（1）错误：内错角不一定相等，
改正：∵∠1和∠2是内错角，DC∥AB，
∴∠1=∠2；

（2）正确，∵∠1=∠2，
∴AB∥CD（两直线平行，内错角相等）．
【点评】本题考查了平行线的判定的应用，能正确根据平行线的判定定理进行推理是解此题的关键，注意：内错角相等，两直线平行．
　
12．（6分）已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，∠BEF的平分线与∠DFE的平分线相交于点P．求证：∠P=90°．

【考点】三角形内角和定理；平行线的性质．
【专题】证明题．
【分析】由AB∥CD，可知∠BEF与∠DFE互补，由角平分线的性质可得∠PEF+∠PFE=90°，由三角形内角和定理可得∠P=90°．
【解答】证明：∵AB∥CD，
∴∠BEF+∠DFE=180°．
又∵∠BEF的平分线与∠DFE的平分线相交于点P，
∴∠PEF=∠BEF，∠PFE=∠DFE，
∴∠PEF+∠PFE=（∠BEF+∠DFE）=90°．
∵∠PEF+∠PFE+∠P=180°，
∴∠P=90°．
【点评】考查综合运用平行线的性质、角平分线的定义、三角形内角和等知识解决问题的能力．
　
13．（6分）如图，∠1=∠2，∠3=∠4，试问EF是否与GH平行？

【考点】平行线的判定．
【分析】求出∠1=∠5，根据平行线的判定得出AB∥CD，根据平行线的性质得出∠AEG=∠CGN，求出∠FEG=∠HGN，根据平行线的判定得出即可．
【解答】解：EF∥GH，
理由是：∵∠1=∠2，∠2=∠5，
∴∠1=∠5，
∴AB∥CD，
∴∠AEG=∠CGN，
∵∠3=∠4，
∴∠AEG﹣∠3=∠CGN﹣∠4，
∴∠FEG=∠HGN，
∴EF∥GH．
【点评】本题考查了平行线的性质和判定的应用，能灵活运用定理进行推理是解此题的关键．
　
14．（6分）如图写出能使AB∥CD成立的各种条件．

【考点】平行线的判定．
【分析】根据平行线的判定（平行线的判定定理有：①同位角相等，两直线平行，②内错角相等，两直线平行，③同旁内角互补，两直线平行）得出即可．
【解答】解：AB∥CD的条件为∠7=∠8或∠3=∠4或∠BAD+∠ADC=180°或∠ABC+∠BCD=180°或∠FAB=∠FDC或∠EDC=∠EAB．
【点评】本题考查了平行线的判定的应用，能熟记平行线的判定定理是解此题的关键，注意：平行线的判定定理有：①同位角相等，两直线平行，②内错角相等，两直线平行，③同旁内角互补，两直线平行．
　
15．（6分）如图，已知AB∥CD，∠1=∠3，试说明AC∥BD．

【考点】平行线的判定与性质．
【专题】推理填空题．
【分析】首先根据两直线平行内错角相等得到∠1=∠2，再根据∠1=∠3得到∠3=∠2，从而判定AC∥BD．
【解答】证明：因为AB∥CD，
所以∠1=∠2，
又因为∠1=∠3，
所以∠3=∠2．
所以AC∥BD．
【点评】本题考查了平行线的判定与性质，解题的关键是牢记平行线的判定与性质定理．
　
16．（6分）已知：如图，∠1=∠2，且BD平分∠ABC．求证：AB∥CD．

【考点】平行线的判定．
【专题】证明题．
【分析】根据平行线的判定方法得出∠1=∠DBA的位置关系即可得出答案．
【解答】证明：∵BD平分∠ABC，
∴∠2=∠DBA，
∵∠1=∠2，
∴∠1=∠DBA，
∴AB∥CD．
【点评】此题主要考查了平行线的判定，熟练掌握平行线的判定得出角之间的关系是解题关键．
　
17．（6分）如图，已知直线a，b，c被直线d所截，若∠1=∠2，∠2+∠3=180°，求证：a∥c．

【考点】平行线的判定与性质．
【专题】证明题．
【分析】求出∠2=∠7，根据平行线的判定推出a∥b，b∥c，即可得出答案．
【解答】证明：∵∠1=∠2，
∴a∥b，
∵∠2+∠3=180°，∠3+∠7=180°，
∴∠2=∠7，
∴b∥c，
∴a∥c．
【点评】本题考查了平行线的判定的应用，能正确根据平行线的判定定理进行推理是解此题的关键，注意：平行于同一直线的两直线平行．
　
18．（6分）如图，已知BE∥CF，BE、CF分别平分∠ABC和∠BCD，求证：AB∥CD．

【考点】平行线的判定与性质；角平分线的定义．
【专题】证明题．
【分析】根据BE∥CF，得∠1=∠2，根据BE、CF分别平分∠ABC和∠BCD，得∠ABC=2∠1，∠BCD=2∠2，则∠ABC=∠BCD，从而证明AB∥CD．
【解答】证明：∵BE∥CF，
∴∠1=∠2．
∵BE、CF分别平分∠ABC和∠BCD，
∴∠ABC=2∠1，∠BCD=2∠2，
即∠ABC=∠BCD，
∴AB∥CD．
【点评】此题综合运用了平行线的性质和判定以及角平分线的定义．
　
19．（6分）已知：如图，AB∥CD，BC∥DE，∠B=70°，求∠D的度数．

【考点】平行线的性质．
【分析】根据平行线的性质即可得到结论．
【解答】解：∵AB∥CD，
∴∠C=∠B=70°，
∵BC∥DE，
∠C+∠D=180°，
∴∠D=110°
【点评】此题主要考查了平行线的判定与性质，关键是掌握平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．
　
20．（6分）已知：BC∥EF，∠B=∠E，求证：AB∥DE．

【考点】平行线的判定与性质．
【专题】证明题．
【分析】根据平行线的性质证得同位角∠E=∠1；然后由等量代换知同位角∠B=∠1；最后根据平行线的判定定理证得结论．
【解答】证明：∵BC∥EF，
∴∠E=∠1．
又∵∠B=∠E，
∴∠B=∠1，
∴AB∥DE．

【点评】本题考查了平行线的判定与性质．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．
　
21．（6分）如图，已知AB∥CD，∠A=100°，CB平分∠ACD，求∠ACD、∠ABC的度数．

【考点】平行线的性质．
【分析】根据平行线的性质求出∠ACD，根据角平分线定义求出∠1、∠2，根据平行线的性质即可求出∠ABC．
【解答】解：∵AB∥CD，∠A=100°，
∴∠ACD=180°﹣∠A=80°，
∵CB平分∠ACD，
∴∠1=∠2=∠ACD=40°，
∵AB∥CD，
∴∠ABC=∠2=40°．
【点评】本题考查了平行线性质的应用，注意：两直线平行，内错角相等，两直线平行，同旁内角互补．
　
22．（6分）如图，已知：DE⊥AO于点E，BO⊥AO于点O，∠CFB=∠EDO，
证明：CF∥DO．

【考点】平行线的判定与性质．
【专题】证明题．
【分析】先由垂直的定义可得：∠AED=∠AOB=90°，然后根据同位角相等，两条直线平行，可得：DE∥BO，进而根据两直线平行，内错角相等，可得∠EDO=∠BOD，然后由等量代换可得：∠BOD=∠CFB，进而由同位角相等，两条直线平行可得：CF∥DO．
【解答】证明：∵DE⊥AO，BO⊥AO，
∴∠AED=∠AOB=90°，
∴DE∥BO（同位角相等，两条直线平行），
∴∠EDO=∠BOD（两直线平行，内错角相等），
∵∠EDO=∠CFB，
∴∠BOD=∠CFB，
∴CF∥DO（同位角相等，两条直线平行）．
【点评】本题考查了平行线的性质和判定的应用，能运用平行线的性质和判定进行推理是解此题的关键，难度适中．