第一章 空间向量与立体几何章末重点题型大总结（精讲）-高二数学上学期同步精讲精练（人教A版2019选择性必修第一册）

第一章 空间向量与立体几何 章末总结（精讲）

目录

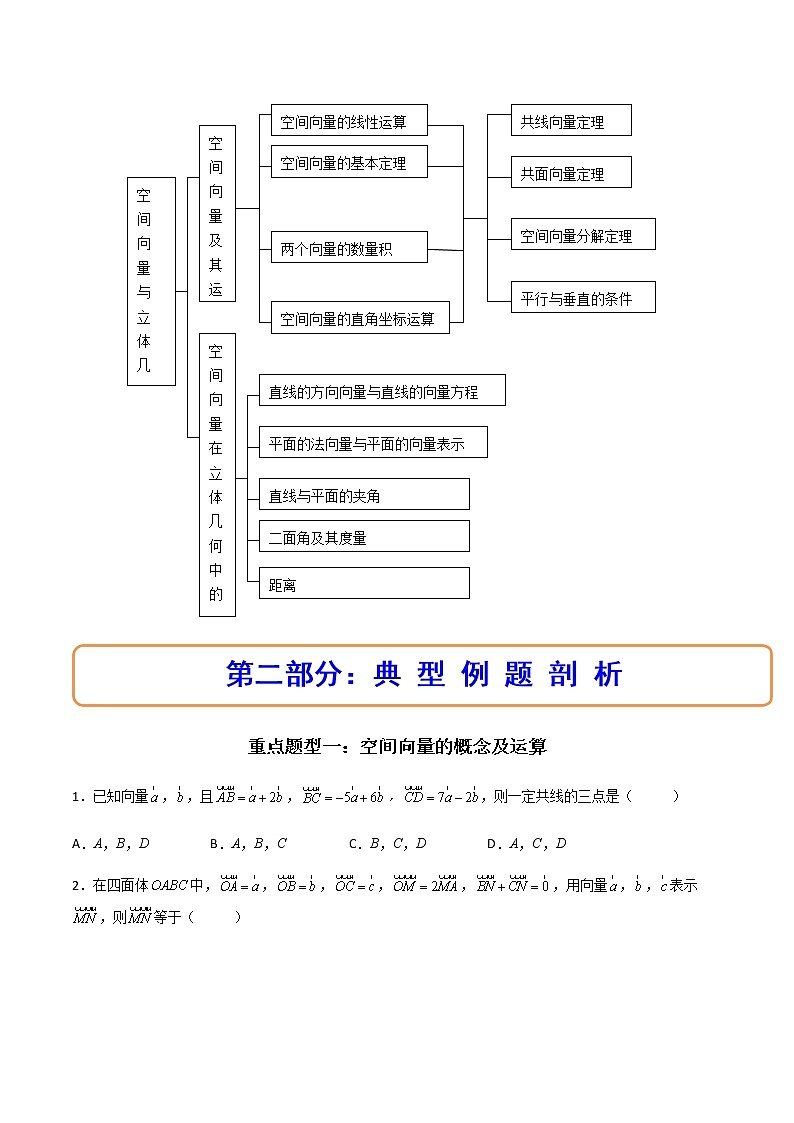
第一部分：本章知识框架

第二部分：典 型 例 题 剖 析

重点题型一：空间向量的概念及运算

重点题型二：利用空间向量证明位置关系

重点题型三：利用空间向量计算距离

重点题型四：利用空间向量求空间角

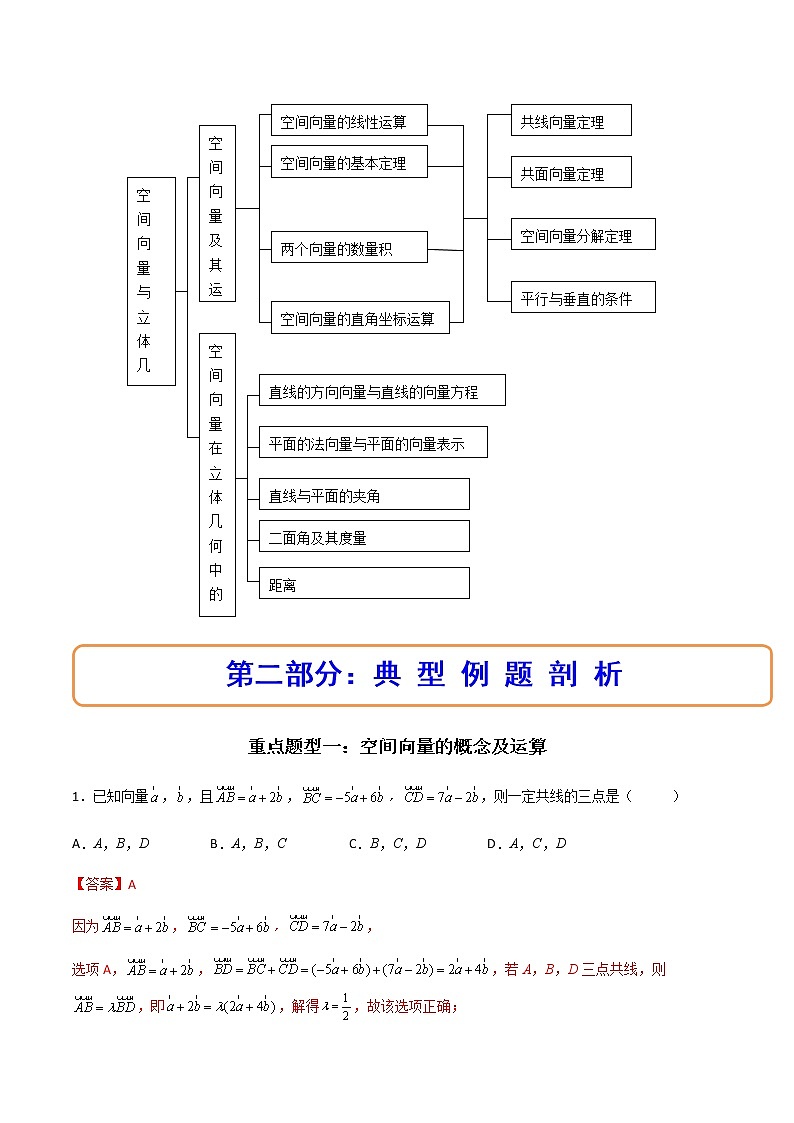
重点题型一：空间向量的概念及运算

1．已知向量，，且，，，则一定共线的三点是（       ）

A．A，B，D B．A，B，C C．B，C，D D．A，C，D

2．在四面体中，，，，，，用向量，，表示，则等于（       ）

A． B．

C． D．

3．如图，在三棱锥中，平面，，，点在三棱锥的表面上运动，则的取值范围是（       ）

A． B． C． D．

4．已知向量，，则下列向量中，使能构成空间的一个基底的向量是（       ）

A． B． C． D．

5．（多选）对空间任意一点和不共线三点，，，能得到，，，四点共面的是（       ）

A． B．

C． D．

6．已知，，若向量，则实数的取值范围为____．

7．已知A，B，C三点不共线，对平面ABC外的任一点O，若点M满足.

（1）判断，，三个向量是否共面；

（2）若三棱锥为棱长为2正四面体，求.

重点题型二：利用空间向量证明位置关系

1．在四棱锥中，，，，，M是AC的中点,若平面平面BCDE，则下列三个结论：①；②；③中，正确的是（       ）

A．①② B．①③ C．②③ D．①②③

2．已知正方体是直线上一点，（       ）

A．若，则直线平面

B．若，则直线平面

C．若，则直线平面

D．若，则直线平面

3．如图正方体中，，，则下列说法不正确的是（       ）

A．时，平面平面

B．时，平面平面

C．面积最大时，

D．面积最小时，

4．已知正方体，是棱的中点，则在棱上存在点，使得（       ）

A． B．

C．平面 D．平面

5．如图，正方体中，点，是上的两个三等分点，点，是上的两个三等分点，点，，分别为，和的中点，点是上的一个动点，下面结论中正确的是___________.

①与异面且垂直；

②与相交且垂直；

③平面；

④，，，四点共面.

6．在平行六面体中，面面，底面为矩形，，，面为菱形，，是的中点，为的中点，问_______时，面面．

7．如图在平行六面体中，，.

(1)求证：直线平面；

8．如图，在长方体中，，，为中点，为中点.求证：平面；

9．如图，在四棱锥中，底面是矩形，平面，，，若M，N分别为棱，的中点，为中点.求证：平面平面

10．已知直三棱柱中，，E，F分别为AC和的中点，D为棱上的点，．

证明：；

重点题型三：利用空间向量计算距离

1．如图所示，ABCD—EFGH为边长等于1的正方体，若P点在正方体的内部且满足，则P点到直线BC的距离为（       ）

A． B． C． D．

2．在三棱锥中，，，，点是的中点，底面，则点到平面的距离为（       ）

A． B． C． D．

3．如图，在棱长为1的正方体中，P为的中点，Q为上任意一点，E，F为CD上两个动点，且EF的长为定值，则点Q到平面PEF的距离（       ）

A．等于 B．和EF的长度有关

C．等于 D．和点Q的位置有关

4．如图所示的多面体，底面ABCD为长方形，DF⊥平面ABCD，DFCC1BE，AB=4，BC=2，CC1=3，BE=1，则点C到平面AEC1F的距离为（       ）

A． B．

C． D．

5．若正方体ABCD­A1B1C1D1的棱长为1，则直线A1C1到平面ACD1的距离为（　　）

A．1 B．

C． D．

6．在棱长为的正方体中，则平面与平面之间的距离为

A． B．

C． D．

7．如图，已知四边形是边长为4的正方形，E，F分别是的中点， 垂直于正方形所在的平面，且，则点B到平面的距离为___________.

8．如图，在长方体中，，，点在棱上移动．

(1)证明：；

(2)当为的中点时，求点到面的距离．

重点题型四：利用空间向量求空间角

角度1：异面直线所成角

1．已知三棱柱的侧棱与底面边长都相等，的中点为，底面，则异面直线与所成角的余弦值为（       ）

A． B． C． D．

2．三棱锥中，，，则异面直线与所成的角可能是（       ）

A．30° B．45° C．60° D．75°

3．如图，在四棱锥中，底面ABCD为矩形，底面，，E为PC的中点，则异面直线PD与BE所成角的余弦值为（       ）

A．  B． C． D．

4．如图，在三棱锥中，平面平面，，，，点是线段上的动点，若线段上存在点，使得异面直线与成30°的角，则线段长的取值范围是（       ）

A． B． C． D．

5．已知动点P在正方体的对角线(不含端点)上.设，若为钝角，则实数的取值范围为（       ）

A． B． C． D．

6．在正方体ABCD—A1B1C1D1中，异面直线和分别在上底面A1B1C1D1和下底面ABCD上运动，且，若与所成角为60°时，则与侧面ADD1A1所成角的大小为（     ）

A．30° B．45° C．60° D．90°

7．如图，在正四棱锥中，二面角为60°，E为的中点.已知F为直线上一点，且F与A不重合，若异面直线与所成角为60°，则=_____________.

8．如图，在长方体中，，，在棱上是否存在一点，使得异面直线与所成角为？若存在，求出点的位置；若不存在，请说明理由．

角度2：线面角

1．在所有棱长都相等的直三棱柱中，、分别为棱、的中点，则直线与平面所成角的余弦值为（       ）

A． B． C． D．

2．如图，在棱长为1的正方体中，为的中点，则直线与平面的夹角为（       ）

A． B． C． D．

3．如图，在四棱柱中，底面为正方形，侧棱底面，，，是侧面内的动点，且，记与平面所成的角为，则的最大值为（       ）

A． B． C．2 D．

4．已知四面体中，，，两两垂直，，与平面所成角的正切值为，则点到平面的距离为（       ）

A． B． C． D．

5．2020年初，新冠肺炎疫情袭击全国，给人民生命财产安全和生产生活造成了严重影响.在党和政府强有力的领导下，全国人民众志成城，取得了抗击疫情战争的重大胜利，社会生产、生活全面恢复正常.某中学结合抗疫组织学生到一工厂开展劳动实习，加工制作临时隔离帐篷.将一块边长为6m的正方形材料先按如图1所示的阴影部分截去四个全等的等腰三角形（其），然后，将剩余部分沿虚线折叠并拼成一个四棱锥型的帐篷（如图2），该四棱锥底面是正方形，从顶点向底面作垂线，垂足恰好是底面的中心.则直线与平面所成角的正弦值为______.

6．如图，菱形ABCD中，∠ABC＝60°，AC与BD相交于点O，AE⊥平面ABCD，CF//AE，AB＝2，CF＝3．若直线OF与平面BED所成的角为45°，则AE＝________．

7．如图，在正四棱柱中，底面边长为2，直线与平面所成角的正弦值为，则正四棱柱的高为_____．

8．如图，四棱锥中，底面为平行四边形，底面，M是棱的中点，且．

(1)求证：平面；

(2)棱上是否存在一点N，使得直线与平面所成角的余弦值为，若存在，求的值；若不存在，说明理由．

9．在正四棱柱中，，E为的中点.（用向量的方法证明）

(1)求证：平面.（用向量的方法证明）

(2)若F为上的动点，使直线与平面所成角的正弦值是，求BF的长.

10．三棱锥中，三角形为等腰直角三角形，，侧面为等边三角形，.

(1)求证：；

(2)若侧棱上有一动点，设，当为何值时，直线与平面所成的角最大？

角度3：二面角

1．已知是各棱长均等于的正三棱柱，是侧棱的中点，则平面与平面所成的锐二面角为（       ）

A．45° B．60° C．75° D．30°

2．如图，在空间直角坐标系中，四棱柱为长方体， ，点为的中点，则二面角的余弦值为（ ）

A． B． C． D．

3．如图，四边形，，，现将沿折起，当二面角的大小在时，直线和所成角为，则的最大值为

A． B． C． D．

4．如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=AA1=2BC=2，D为AA1上一点.若二面角B1-DC-C1的大小为30°，则AD的长为____. 

5．如图，在四棱柱中，底面ABCD和侧面都是矩形，E是CD的中点，，若平面与平面所成的锐二面角的大小为，则线段的长度为__________．

6．如图，平面平面是边长为4的正三角形，分别为的中点.

(1)求证：；

(2)求平面与平面的夹角的大小.

7．如图，四棱柱中，侧棱底面ABCD，，，，，E为棱的中点．

(1)证明：；

(2)求平面与平面夹角的正弦值；

(3)设点M在线段上，且直线AM与平面所成角的正弦值为，求线段AM的长．

8．如图，在四棱锥中，侧面为等边三角形，底面为等腰梯形，且

(1)证明：平面平面；

(2)若点在棱上，且二面角的大小为，求的值.

9．如图，在四棱锥中，底面是等腰梯形，，与交点为，且，．

（1）证明：平面；

（2）若且，，则在线段上是否存在一点﹐使得二面角的余弦值为，若存在，求出点的位置；若不存在，请说明理由．

10．如图①，在等腰梯形中，，.将沿折起，使得，如图②.

（1）求证：平面平面.

（2）在线段上是否存在点，使得二面角的平面角的大小为？若存在，指出点的位置；若不存在，请说明理由.