人教A版 (2019)2.5 直线与圆、圆与圆的位置精品课堂检测

这是一份人教A版 (2019)2.5 直线与圆、圆与圆的位置精品课堂检测，文件包含252圆与圆的位置关系精讲解析版docx、252圆与圆的位置关系精讲原卷版docx等2份试卷配套教学资源，其中试卷共52页， 欢迎下载使用。
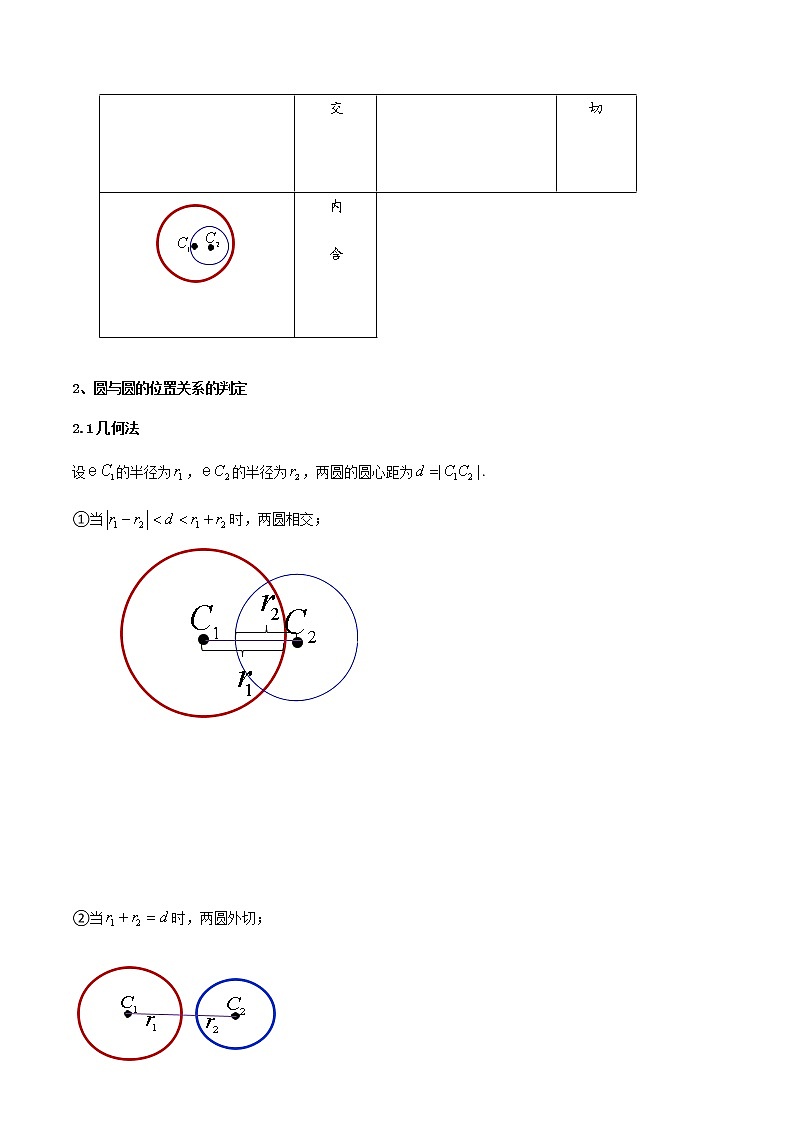
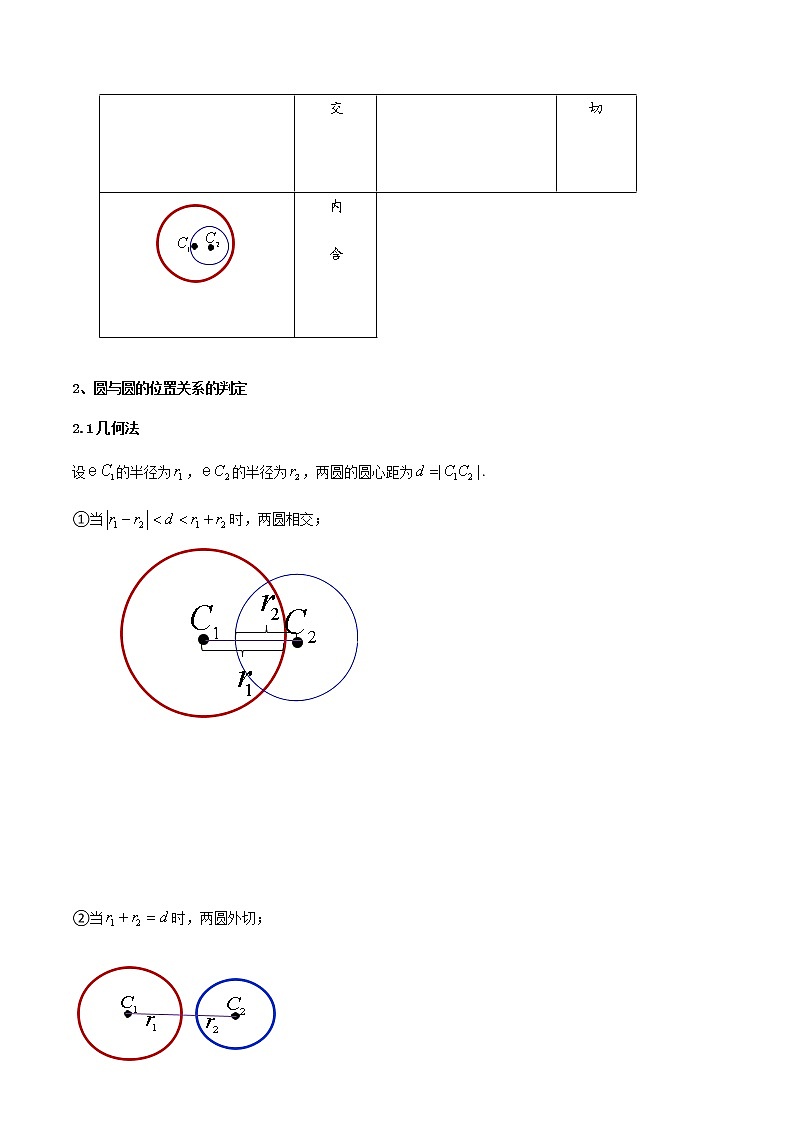
2.5.2圆与圆的位置关系（精讲）目录第一部分：思维导图（总览全局）第二部分：知识点精准记忆第三部分：课前自我评估测试第四部分：典 型 例 题 剖 析重点题型一：两圆的位置关系重点题型二：两圆相切问题重点题型三：两圆相交的公共弦所在直线的方程及弦长重点题型四：圆与圆的位置关系的应用第五部分：高考（模拟）题体验  知识点一：圆与圆的位置关系1、圆与圆的位置关系(1)圆与圆相交，有两个公共点；(2)圆与圆相切(内切或外切)，有一个公共点；(3)圆与圆相离(内含或外离)，没有公共点.图象位置关系图象位置关系   外离 外切   相交 内切   内含 2、圆与圆的位置关系的判定2.1几何法设的半径为，的半径为，两圆的圆心距为.①当时，两圆相交；         ②当时，两圆外切；     ③当时，两圆外离；     ④当时，两圆内切；      ⑤当时，两圆内含.     2.2代数法设::联立消去“”得到关于“”的一元二次方程，求出其①与设设相交②与设设相切（内切或外切）③与设设相离（内含或外离）知识点二：圆与圆的公共弦1、圆与圆的公共弦圆与圆相交得到的两个交点，这两点之间的线段就是两圆的公共弦.2、公共弦所在直线的方程设::联立作差得到：即为两圆共线方程3、公共弦长的求法代数法：将两圆的方程联立，解出两交点的坐标，利用两点间的距离公式求其长．几何法：求出公共弦所在直线的方程，利用勾股定理解直角三角形，求出弦长．知识点三：圆与圆的公切线1、公切线的条数与两个圆都相切的直线叫做两圆的公切线，圆的公切线包括外公切线和内公切线两种．（1）两圆外离时，有2条外公切线和2条内公切线，共4条；      （2）两圆外切时，有2条外公切线和1条内公切线，共3条；      （3）两圆相交时，只有2条外公切线；   （4）两圆内切时，只有1条外公切线；     （5）两圆内含时，无公切线．    2、公切线的方程核心技巧：利用圆心到切线的距离求解知识点四：圆系方程 以为圆心的同心圆圆系方程：； 与圆同心圆的圆系方程为； 过直线与圆交点的圆系方程为  过两圆，圆：交点的圆系方程为（，此时圆系不含圆：）特别地，当时，上述方程为一次方程.两圆相交时，表示公共弦方程；两圆相切时，表示公切线方程.1．（2022·全国·高二课时练习）判断正误（1）若两圆没有公共点，则两圆一定外离．(      )（2）若两圆外切，则两圆有且只有一个公共点，反之也成立．(      )（3）若两圆有公共点，则．(      )2．（2022·江西·贵溪市实验中学高二期末）圆：与圆：的位置关系是内切   (        ) 3．（2022·全国·高二课时练习）圆与圆的内公切线有且仅有(        )A．1条          B．2条          C．3条          D．4条4．（2022·全国·高二课时练习）若两圆的半径R，r分别为5和2，圆心距d为3，则两圆的位置关系是_________．5．（2022·全国·高二课时练习）圆与圆的位置关系是(        )A．相交          B．外离          C．外切            D．内切重点题型一：两圆的位置关系角度1：判断两圆位置关系典型例题例题1．（2022·天津河北·高二期末）已知圆与圆，则两圆的位置关系是（   ）A．外切 B．内切 C．相交 D．相离例题2．（2022·福建福州·高二期末）圆与圆的公切线的条数为（  ）A．1 B．2 C．3 D．4例题3．（2022·江苏·高二）两圆与的公切线有（   ）A．1条 B．2条 C．3条 D．4条角度2：由圆的位置关系求参数典型例题例题1．（2022·全国·高三专题练习）已知圆：和圆：有且仅有4条公切线，则实数的取值范围是（  ）A． B．C． D． 例题2．（2022·全国·高三专题练习）“”是“与相切”的（  ）A．充分不必要条件 B．必要不充分条件 C．充分且必要条件 D．既不充分又不必要条件例题3．（2022·江苏·高二）若圆与圆相外切，则的值为（    ）A． B． C．1 D．例题4．（2022·江苏盐城·高二期末）若圆和圆有两个不同的公共点，则实数的取值范围是___________.  同类题型归类练1．（2022·全国·高二期中）若圆x2＋y2－2ax＋a2＝2和x2＋y2－2by＋b2＝1外离，则a，b满足的条件是________________．2．（2022·全国·高三专题练习）若圆与圆内切，则_________.3．（2022·安徽·合肥市第七中学高二期末）已知圆，圆，则两圆的公切线条数是___________.4．（2022·全国·高三专题练习）两圆与相交，则的取值范围是______.5．（2022·全国·高三专题练习（文））已知圆与圆外切,则的值为______.6．（2022·全国·高三专题练习）已知圆C1：x2＋y2＋4ax＋4a2－4＝0和圆C2：x2＋y2－2by＋b2－1＝0只有一条公切线，则4a2＋b2＝________． 重点题型二：两圆相切问题例题1．（2022·上海徐汇·高二期末）已知圆和圆内切，则的值为___________．例题2．（2022·全国·高三专题练习）已知圆与圆，若圆与圆相外切，则实数＝________.例题3．（2022·全国·高三专题练习）已知圆:与圆：相内切， 则 的最小值为__________．   同类题型归类练1．（2022·全国·高三专题练习）半径为6的圆与x轴相切，且与圆内切，则此圆的方程为______2．（2022·天津市西青区杨柳青第一中学高三阶段练习）已知圆与圆外切，则实数a的值为___________.3．（2022·江苏盐城·高二期末）已知圆C1：(x－a)2＋(y＋2)2＝4与圆C2：(x＋b)2＋(y＋2)2＝1外切，则ab的最大值为_____________．4．（2022·全国·高二课时练习）求以为圆心，且与圆相外切的圆C的方程．5．（2022·全国·高二课时练习）已知圆与圆外切，求实数a的值． 重点题型三：两圆相交的公共弦所在直线的方程及弦长角度1：求公共弦方程典型例题例题1．（2022·浙江·高三专题练习）圆与圆的公共弦所在直线方程______．例题2．（2022·全国·高二）已知圆，圆的圆心在轴上，且与的公共弦所在直线的方程为，则圆的方程为___________.   角度2：两圆公共弦长典型例题例题1．（2022·天津河北·二模）圆和圆的公共弦的长为___________．例题2．（2022·天津市第四十七中学高三开学考试）若圆与圆()的公共弦长为，则＝________.   同类题型归类练1．（2022·河北·张家口市宣化第一中学高二期末）若圆和圆的公共弦所在的直线方程为，则______．2．（2022·全国·高三专题练习）已知两圆C1：x2＋y2－2x＋10y－24＝0，C2：x2＋y2＋2x＋2y－8＝0，则两圆公共弦所在的直线方程是____________．3．（2022·黑龙江·鸡东县第二中学高二开学考试）已知圆与相交，它们公共弦所在直线的方程是________．4．（2022·广东汕头·高二阶段练习）圆与的公共弦长为（       ）A． B． C． D．5．（2022·山东威海·三模）圆与圆的公共弦长为______．6．（2022·四川省广安代市中学校高二阶段练习（理））若圆x2＋y2＝4与圆x2＋y2＋2x＋2ay－6＝0( )的公共弦长为，则a＝________.7．（2022·贵州毕节·模拟预测（理））已知圆与圆（t，m，）相交于P，Q两点（点M与点N在直线PQ两侧），且，则的最大值是（       ）A． B． C． D． 重点题型四：圆与圆的位置关系的应用角度1：圆的公切线条数典型例题例题1．（2022·陕西·西安中学一模（理））在平面直角坐标系中，圆：与圆：，则两圆的公切线的条数是（   ）A．4条 B．3条 C．2条 D．1条例题2．（2022·四川宜宾·高二期末（理））若圆与圆有且仅有一条公切线，则（   ）A．－23 B．－3 C．－12 D．－13    角度2：圆的公切线方程典型例题例题1．（2022·江苏·高二）写出与圆和都相切的一条直线的方程________________．   角度3：圆的公切线长典型例题例题1．（2022·吉林·长春吉大附中实验学校高二阶段练习）在平面直角坐标系中，已知圆：，：，及点和.(1)求圆和圆公切线段的长度；   角度4：与圆有关的最值问题典型例题例题1．（2022·全国·高二课时练习）已知圆和圆，分别是圆上的动点，为轴上的动点，则的最小值为（  ）A． B． C． D．例题2．（2022·全国·高三专题练习）点是圆上的任一点，圆是过点且半径为1的动圆，点是圆上的任一点，则长度的最小值为（  ）A．1 B．2 C．3 D．4    同类题型归类练1．（2022·四川·成都七中模拟预测（理））圆与圆的公切线条数为（       ）A．1 B．2 C．3 D．42．（2022·全国·高三专题练习）若圆与圆恰有2条公切线，则的取值范围为（       ）A． B． C． D．3．（2022·广东广州·高二期末）写出与圆和圆都相切的一条切线方程___________.4．（2021·安徽·池州市第一中学高二期中）已知圆，(1)判断两圆的位置关系，并求它们的公切线之长；        5．（2022·陕西·无高一阶段练习）若，分别为圆：与圆：上的动点，为直线上的动点，则的最小值为（       ）A． B．6 C．9 D．126．（2022·河南·模拟预测（理））过圆上的点P作圆的切线，切点为Q，则的最小值为（       ）A．2 B． C． D．   1．（2022·全国·模拟预测）若圆与单位圆恰有三条公切线，则实数a的值为（       ）A． B．2 C． D．2．（2022·河南·开封市东信学校模拟预测（文））已知直线，过直线l上的动点P作圆的两条切线，切点分别为A，B，则点到直线的距离最大值为（       ）A． B． C． D．3．（多选）（2022·全国·模拟预测）已知点在圆上，点，，则（       ）A．点到直线的距离最大值为B．满足的点有3个C．过点作圆的两切线，切点分别为､，则直线的方程为D．的最小值是4．（2022·天津二中模拟预测）已知圆与圆外切，此时直线被圆所截的弦长_________．5．（2022·陕西·交大附中模拟预测（理））已知在平面直角坐标系中，点，直线．设圆的半径为，圆心在直线上．(1)若圆心也在直线上，过点作圆的切线，求切线的方程；(2)若圆上存在点，使，求圆心的横坐标的取值范围．