青岛版九年级下册5.3二次函数教课内容课件ppt

这是一份青岛版九年级下册5.3二次函数教课内容课件ppt，共18页。PPT课件主要包含了学习目标，温故知新，变量之间的关系，一次函数，反比例函数，观察与思考，s2t2，例题讲解，课堂小结，达标练习等内容，欢迎下载使用。
1.结合具体情境，通过用解析法表示简单实际问题中变量之间的二次函数关系，体会二次函数的意义.2.经历二次函数概念的形成过程，体会二次函数也是一种数学模型.3.会把一个二次函数化成一般形式.
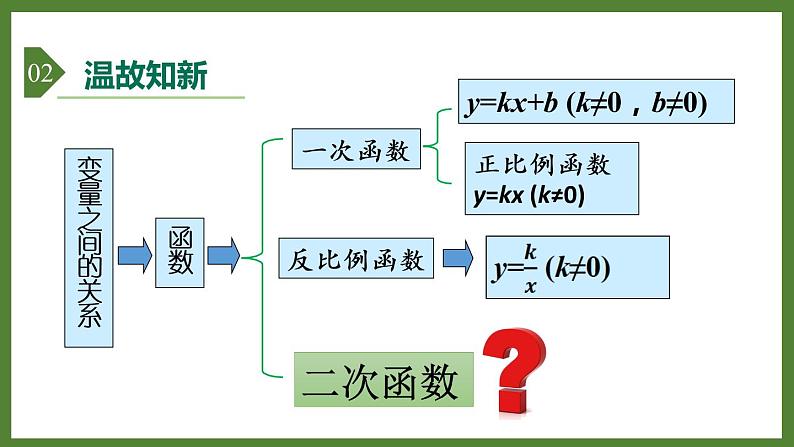
y=kx+b (k≠0，b≠0)
正比例函数y=kx (k≠0)
思考下列问题，并与同学交流.(1)把一根长为60cm的铁丝，围成一个矩形，写出矩形的面积S(cm2)与它的一边长x(cm)之间的函数表达式.
解：(1)矩形的一边长为xcm,则它的另一边长为(30-x)cm, 因此矩形的面积S=x(30-x), 整理得S=-x2+30x.
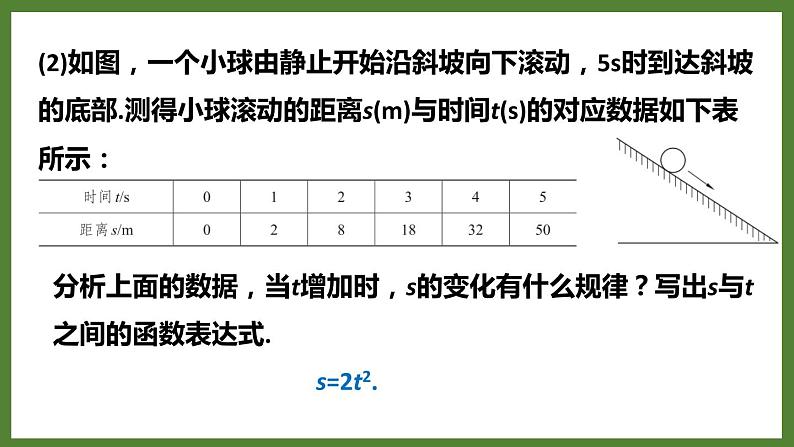
(2)如图，一个小球由静止开始沿斜坡向下滚动，5s时到达斜坡的底部.测得小球滚动的距离s(m)与时间t(s)的对应数据如下表所示：
分析上面的数据，当t增加时，s的变化有什么规律？写出s与t之间的函数表达式.
(3)某企业去年的产值为1200万元.如果三年内该企业年产值平均每年的增长率为x，写出明年该企业年产值y(万元)与x之间的函数表达式.
(3)因为去年的年产值为1200万元，所以该企业今年的年产值为1200+1200x，即1200(1+x).因而，明年该企业的年产值y(万元)与增长率x之间的函数表达式为y=1200(1+x)+1200(1+x) ·x=1200(1+x)2.进一步整理得到：y=1200x2+2400x+1200.
(4)上面三个问题中的函数表达式分别为：S=-x2+30x， s=2t2，y=1200x2+2400x+1200.观察这些函数表达式，它们具有什么共同特征？
这些函数表达式都是关于自变量的二次整式.
一般地，形如y=ax2+bx+c(a,b,c是常数，且a≠0)的函数叫做二次函数.其中，a为二次项系数，b为一次项系数，c为常数项.
(5)说出二次函数y=ax2+bx+c中自变量x的取值范围，再分别说出问题(1)(2)(3)中自变量可以取值的范围.
在一般形式下，由于二次函数的表达式是整式，所以x取任意一个实数时，函数y都有意义，即自变量的取值范围是全体实数.
问题(1): 一边长x应满足0＜x＜30；问题(2): t的取值范围是0≤t≤5;问题(3): x的取值范围是x＞0.
二次函数y=ax2+bx+c的自变量x可以取值的范围是全体实数，但在具体问题中，还要结合实际背景确定自变量的取值范围.
1.下列函数中,哪些是二次函数？
(1)y=3(x-1) 2+1;
(2) s=3-2t2;
(3) y=(x+3) 2-x2；
(4) v=10πr2;
(7) y=ax2+bx+c.
(6)y=22+2x;
判断一个函数是否是二次函数，看它是否能化简成y=ax2+bx+c(a、b、c为常数且a≠0)的形式.
(5) y=x2+x³+25；
2.写出下列三个二次函数表达式中的二次项系数、一次项系数和常数项.
例1 如图，从半径为15的圆形铁片上，挖去一个半径为x的圆.写出剩余部分的面积y与x之间的函数表达式，并指出自变量x可以取值的范围.
解：原来圆形铁片的面积为S=π×152=225π，挖去部分的面积为πx2.所以，剩余部分的面积y与x之间的函数表达式为y=225π-πx2=-πx2+225π.根据题意，小圆在大圆的内部，所以自变量x可以取值的范围是0＜x＜15.
例2 已知函数 y= (m+3)xm2-7 . (1)m取什么值时，此函数是二次函数？(2)m取什么值时，此函数是正比例函数？(3)m取什么值时，此函数是反比例函数？
通过本节课的学习，你有哪些收获？
1.二次函数定义：一般地，形如y=ax²+bx+c(a,b,c是常数,a≠0)的函数叫做二次函数.
2.判断一个函数是否为二次函数的方法与步骤：
(1)先将函数进行整理，使其右边是含自变量的代数式， 左边是因变量；
(2)判断含自变量的代数式是否为整式；
(4)判断二次项的系数是否为0.
(3)判断含自变量的项的最高次数是否为2；
解析：一定是二次函数的是①②⑤⑥.
2.把一根长为50cm的铁丝弯成一个长方形，设这个长方形的一边长为x(cm),它的面积为y(cm2),则y与x之间的函数表达式为( )A.y=-x2+50x B.y=x2-50xC.y=-x2+25x D.y=-2x2+25
解析：因为这个长方形的一边长为xcm,所以另一边长为(25-x)cm,故面积y=x(25-x)=-x2+25x.